24.1中心投影与平行投影 课件(共24张PPT)
文档属性
| 名称 | 24.1中心投影与平行投影 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 15:03:56 | ||
图片预览







文档简介
(共24张PPT)
24.1 中心投影与平行投影
主讲:
京改版九年级下册
第24章 投影、视图与展开图
章节导入
物体在光的映照下会留下影子,这是我们非常熟悉的生活现象 . 人们将这一现象加以科学抽象,得出投影法则,并广泛用于艺术和工程制图之中 . 在本章我们将从影子说起,了解一些投影的基本概念,进而学习基本
几何体的三视图和平面展开图 .
学习目标
目标
1
目标
2
1.掌握平行投影的定义及特点;
目标
3
2.掌握中心投影的定义及特点;
3.掌握平行投影、中心投影的作图。
自学指导
仔细阅读教材P38---P41。用3分钟的时间看谁又快又好地解决以下问题:
1.什么平行投影?
2.什么是中心投影?
实践
探究新知
如下,物体在灯光或日光的照射下会在某个平面(屏幕、墙壁、地面等)留下影子,而且影子与物体本身的形状有密切的几何关系,这就是生活中常见的投影现象,这个影子就是我们所说的物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面。
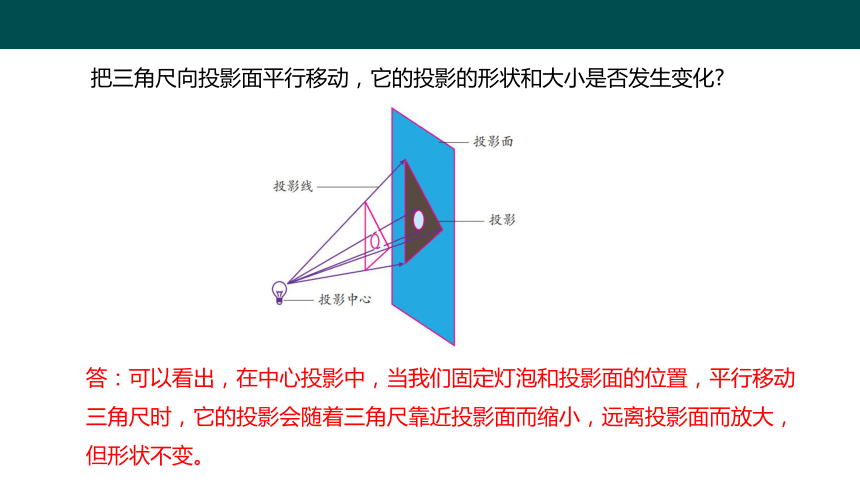
下图是三角尺在灯光照射下形成的投影示意图。灯的光线可以看做是从一点发出的,我们把这种投影称为中心投影,这个点称为投影中心。
知识要点
把三角尺向投影面平行移动,它的投影的形状和大小是否发生变化
答:可以看出,在中心投影中,当我们固定灯泡和投影面的位置,平行移动三角尺时,它的投影会随着三角尺靠近投影面而缩小,远离投影面而放大,但形状不变。
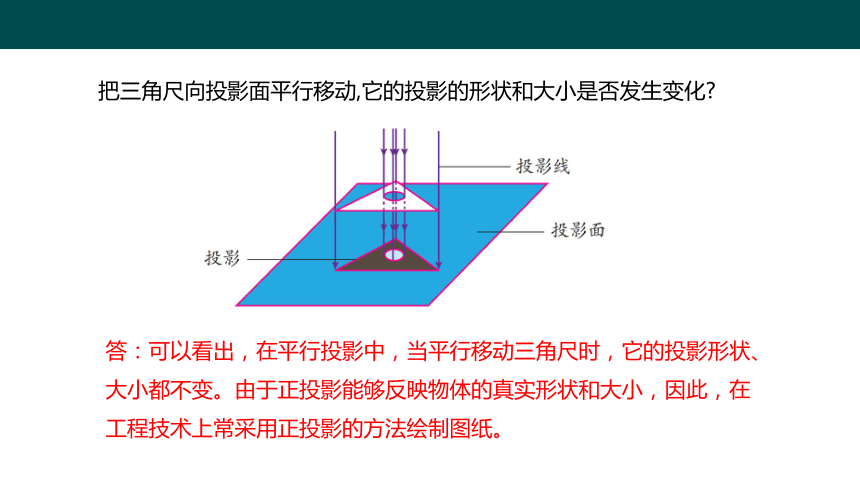
由于太阳离我们很远,它的光线可以看做是平行的,我们把在太阳光照射下形成的这种投影称为平行投影。如下图,在平行投影中,如果投影线与投影面垂直,那么这种投影称为正投影。
知识要点
把三角尺向投影面平行移动,它的投影的形状和大小是否发生变化
答:可以看出,在平行投影中,当平行移动三角尺时,它的投影形状、大小都不变。由于正投影能够反映物体的真实形状和大小,因此,在工程技术上常采用正投影的方法绘制图纸。
例1 如下图1和图2,分别是在同一时刻木杆的影子,辨认哪幅图所示的投影是中心投影,哪幅图所示的投影是平行投影?
典型例题
图1
图2
解:如图1,分别连接 AA'和 BB',并延长 A'A、B'B,可以发现 A'A与 B'B交于点 P,即光是从点 P发出的,因此,图1所示的投影是中心投影。
图1
图2
如图2,分别连接CC'和 DD',并延长 C'C、D'D,可以发现C'C∥D'D即光线平行,因此,图2所示的投影是平行投影。
例2 如图,分别画出线段 AB与投影面平行、倾斜和垂直时的正投影,并比较线段 AB与其投影的大小.
典型例题
解:可将点A的投影点记作A',点B的投影点记作B',则线段 AB的投影可记作A'B'.
如图,当AB与投影面平行时,线段AB与其投影A'B'相等,即A'B'=AB.
当 AB与投影面倾斜时,它的投影缩短,即A'B'平行投影和中心投影有什么区别和联系呢
区别 联系
光线 物体与投影面平行时的投影 中心投影 从一点出发的投射线 放大(位似变换) 都是物体在光线的照射下,在某个平面内形成的影子。(即都是投影)
平行投影 平行的投射线 光线与投影面垂直:全等 思考
典型例题
例3 同一时刻,两根木棒的影子如图,请画出图中另一根木棒的影子。
解:作图如下:
基础检测
1.下列投影一定不会改变△ABC的形状和大小的是( )
A.中心投影
B.平行投影
C.当△ABC平行于投影面时的正投影
D.当△ABC平行于投影面时的中心投影
2.下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A
B
C
B
C
D
2.根据要求完成下列图片:用线段表示出小红行至B处时,她在路灯A下的影子.
C
B
A
3.矩形木框在阳光照射下,在地面上的影子不可能是( )。
C
A
B
C
D
1.如图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA的长度为( )米.
A. B. C. D.2
一展身手
B
2.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆.当把球向下平移时,圆形阴影的大小的变化情况是( )
A.越来越小
B.越来越大
C.大小不变
D.不能确定
A
P
与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子,树影是路灯灯光形成的。你能确定此时路灯光源的位置吗?
挑战自我
课堂小结
平行投影和中心投影
1.平行投影的定义及特点;
2.中心投影的定义及特点;
3.平行投影与中心投影的作图。
主讲:
感谢聆听
京改版九年级下册
24.1 中心投影与平行投影
主讲:
京改版九年级下册
第24章 投影、视图与展开图
章节导入
物体在光的映照下会留下影子,这是我们非常熟悉的生活现象 . 人们将这一现象加以科学抽象,得出投影法则,并广泛用于艺术和工程制图之中 . 在本章我们将从影子说起,了解一些投影的基本概念,进而学习基本
几何体的三视图和平面展开图 .
学习目标
目标
1
目标
2
1.掌握平行投影的定义及特点;
目标
3
2.掌握中心投影的定义及特点;
3.掌握平行投影、中心投影的作图。
自学指导
仔细阅读教材P38---P41。用3分钟的时间看谁又快又好地解决以下问题:
1.什么平行投影?
2.什么是中心投影?
实践
探究新知
如下,物体在灯光或日光的照射下会在某个平面(屏幕、墙壁、地面等)留下影子,而且影子与物体本身的形状有密切的几何关系,这就是生活中常见的投影现象,这个影子就是我们所说的物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面。
下图是三角尺在灯光照射下形成的投影示意图。灯的光线可以看做是从一点发出的,我们把这种投影称为中心投影,这个点称为投影中心。
知识要点
把三角尺向投影面平行移动,它的投影的形状和大小是否发生变化
答:可以看出,在中心投影中,当我们固定灯泡和投影面的位置,平行移动三角尺时,它的投影会随着三角尺靠近投影面而缩小,远离投影面而放大,但形状不变。
由于太阳离我们很远,它的光线可以看做是平行的,我们把在太阳光照射下形成的这种投影称为平行投影。如下图,在平行投影中,如果投影线与投影面垂直,那么这种投影称为正投影。
知识要点
把三角尺向投影面平行移动,它的投影的形状和大小是否发生变化
答:可以看出,在平行投影中,当平行移动三角尺时,它的投影形状、大小都不变。由于正投影能够反映物体的真实形状和大小,因此,在工程技术上常采用正投影的方法绘制图纸。
例1 如下图1和图2,分别是在同一时刻木杆的影子,辨认哪幅图所示的投影是中心投影,哪幅图所示的投影是平行投影?
典型例题
图1
图2
解:如图1,分别连接 AA'和 BB',并延长 A'A、B'B,可以发现 A'A与 B'B交于点 P,即光是从点 P发出的,因此,图1所示的投影是中心投影。
图1
图2
如图2,分别连接CC'和 DD',并延长 C'C、D'D,可以发现C'C∥D'D即光线平行,因此,图2所示的投影是平行投影。
例2 如图,分别画出线段 AB与投影面平行、倾斜和垂直时的正投影,并比较线段 AB与其投影的大小.
典型例题
解:可将点A的投影点记作A',点B的投影点记作B',则线段 AB的投影可记作A'B'.
如图,当AB与投影面平行时,线段AB与其投影A'B'相等,即A'B'=AB.
当 AB与投影面倾斜时,它的投影缩短,即A'B'
区别 联系
光线 物体与投影面平行时的投影 中心投影 从一点出发的投射线 放大(位似变换) 都是物体在光线的照射下,在某个平面内形成的影子。(即都是投影)
平行投影 平行的投射线 光线与投影面垂直:全等 思考
典型例题
例3 同一时刻,两根木棒的影子如图,请画出图中另一根木棒的影子。
解:作图如下:
基础检测
1.下列投影一定不会改变△ABC的形状和大小的是( )
A.中心投影
B.平行投影
C.当△ABC平行于投影面时的正投影
D.当△ABC平行于投影面时的中心投影
2.下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A
B
C
B
C
D
2.根据要求完成下列图片:用线段表示出小红行至B处时,她在路灯A下的影子.
C
B
A
3.矩形木框在阳光照射下,在地面上的影子不可能是( )。
C
A
B
C
D
1.如图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.6米,车头FACD近似看成一个矩形,且满足3FD=2FA,若盲区EB的长度是6米,则车宽FA的长度为( )米.
A. B. C. D.2
一展身手
B
2.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆.当把球向下平移时,圆形阴影的大小的变化情况是( )
A.越来越小
B.越来越大
C.大小不变
D.不能确定
A
P
与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子,树影是路灯灯光形成的。你能确定此时路灯光源的位置吗?
挑战自我
课堂小结
平行投影和中心投影
1.平行投影的定义及特点;
2.中心投影的定义及特点;
3.平行投影与中心投影的作图。
主讲:
感谢聆听
京改版九年级下册
