24.3基本几何体的平面展开图(几何体展开、图形折叠等3大题型提分练) 课件(共23张PPT)
文档属性
| 名称 | 24.3基本几何体的平面展开图(几何体展开、图形折叠等3大题型提分练) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
24.3基本几何体的平面展开图
主讲:
京改版九年级下册
第24章 投影、视图与展开图
章节导入
答:一般地,我们把从物体正面得到的视图称为主视图,从物体的左侧面得到的视图称为左视图,从物体上面得到的视图称为俯视图,把它们统称为三视图 .
请你回忆上一节的内容,什么是三视图?
学习目标
目标
1
目标
2
1.掌握常见几何体的展开图;
目标
3
2.理解如何将展开图折叠成几何体;
3.掌握展开与折叠的相关应用。
自学指导
仔细阅读教材P48---P50。用3分钟的时间看谁又快又好地解决以下问题:
1.长方体的展开图是怎样的?
实践
探究新知
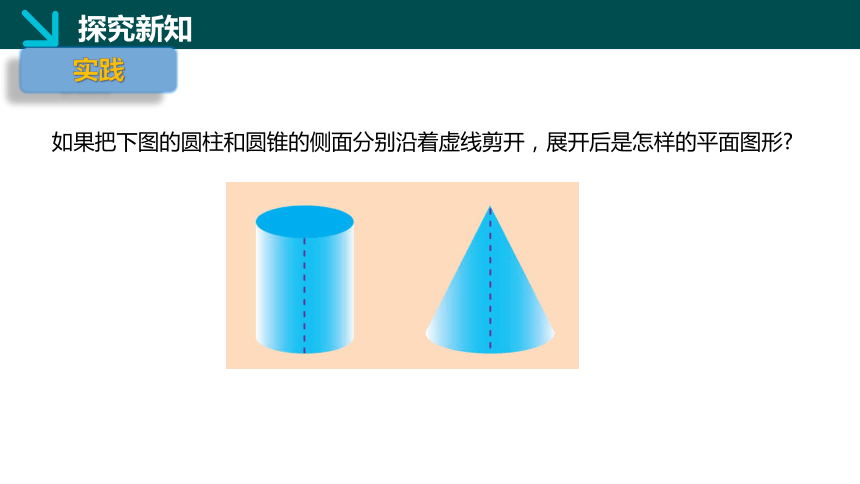
如果把下图的圆柱和圆锥的侧面分别沿着虚线剪开,展开后是怎样的平面图形
一个圆柱的侧面展开图是一个矩形,如图1所示;
一个圆锥的侧面展开图是一个扇形,如图2所示.
图1
图2
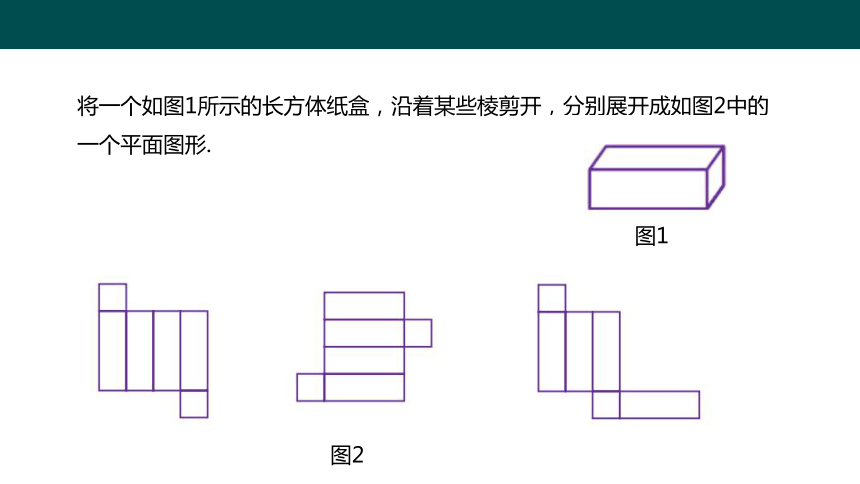
将一个如图1所示的长方体纸盒,沿着某些棱剪开,分别展开成如图2中的一个平面图形.
图1
图2
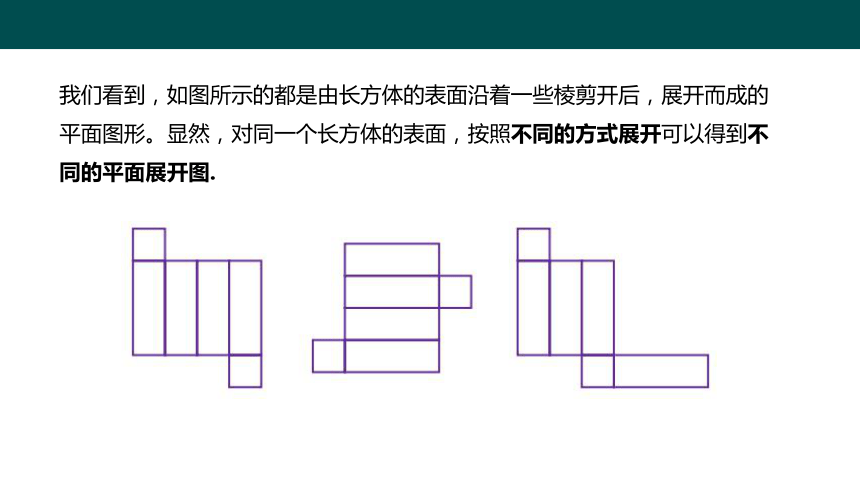
我们看到,如图所示的都是由长方体的表面沿着一些棱剪开后,展开而成的平面图形。显然,对同一个长方体的表面,按照不同的方式展开可以得到不同的平面展开图.
1.一个正三棱锥的表面可以展开成如下图中的哪个平面图形
交流
答:图1.
2.下图所示的平面图形中,哪些能围成一个正方体
答:图1、图2、图3.
某灯具厂要制作一批灯具,设计师给出了如图1所示的灯具三视图的示意图,试按照三视图确定制作每个灯具所需材料的面积 ( 精确到 0. 1m2) .
分析: 在本题中,如果知道每个灯具的侧面积和底面积,就可知道制作每个灯具所需材料的总面积 . 因此,解决本题的思路是先由三视图判断出灯具的立体模型,然后再由立体模型画出它的一个平面展开图,从而计算出它的总面积 .
图1
典型例题
解:由图1可知,灯具是正三棱柱形状 . 如图2所示,其上、下底是相同的等边三角形,三个侧面是相同的矩形,而且矩形的长为6m、宽为 4 m,等边三角形的边长为6m,所以可得到这个正三棱柱灯具的一个平面展开图,如图。
图1
图2
由展开图可知,制作一个灯具所需材料的面积为
( × 6 × 6sin60°) × 2 + ( 4 × 6 ) × 3
≈ 103. 2 ( m2 ).
答:制作每个灯具所需材料的面积约为 103. 2 m2 .
解:(1)侧面数(4个)≠底面边数(3条),不能围成棱柱.
(2)两底面在侧面展开图的同一端,不在两端,所以也不能围成棱柱.
(3)可以折成棱柱。
1.下面图形经过折叠能否围成棱柱?
基础检测
2.下面几个图形是一些常见几何体的展开图,你能正确说出这些几何体的名字么?
圆锥 四棱锥 长方体 三棱柱
三棱锥 三棱柱 正方体 圆柱
3.如图,上面的图形分别是下面哪个立体图形展开的形状?把它们用线连起来.
4.下图是一些立体图形的展开图,用它们能围成怎样的立体图形?
正方体
圆柱
三棱柱
圆锥
一展身手
1.右图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( )。
A. B. C. D.
B
2.下图是一个正方体的平面展开图,如果使字母 A 出现在顶面,那么它的底面应该出现什么字母?
答:底面是F。
A
N
M
L
K
J
I
H
G
F
E
D
C
B
3.把左图中长方体的表面展开图,折叠成一个长方体,那么与字母 J重合的点是哪几个?
答:与J重合的点有:H , N
挑战自我
A
1
-4
3
-
2
1.下图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,求x的值.
A
1
-4
3
-
2
3x+2
解:依题意得,正方体的左面为-4,右面为3x+2,
即3x+2=-4,
解得x=-2.
课堂小结
比例基本几何体的平面展开图
1.常见几何体的展开图;
2.将展开图折叠成几何体。
主讲:
感谢聆听
京改版九年级下册
24.3基本几何体的平面展开图
主讲:
京改版九年级下册
第24章 投影、视图与展开图
章节导入
答:一般地,我们把从物体正面得到的视图称为主视图,从物体的左侧面得到的视图称为左视图,从物体上面得到的视图称为俯视图,把它们统称为三视图 .
请你回忆上一节的内容,什么是三视图?
学习目标
目标
1
目标
2
1.掌握常见几何体的展开图;
目标
3
2.理解如何将展开图折叠成几何体;
3.掌握展开与折叠的相关应用。
自学指导
仔细阅读教材P48---P50。用3分钟的时间看谁又快又好地解决以下问题:
1.长方体的展开图是怎样的?
实践
探究新知
如果把下图的圆柱和圆锥的侧面分别沿着虚线剪开,展开后是怎样的平面图形
一个圆柱的侧面展开图是一个矩形,如图1所示;
一个圆锥的侧面展开图是一个扇形,如图2所示.
图1
图2
将一个如图1所示的长方体纸盒,沿着某些棱剪开,分别展开成如图2中的一个平面图形.
图1
图2
我们看到,如图所示的都是由长方体的表面沿着一些棱剪开后,展开而成的平面图形。显然,对同一个长方体的表面,按照不同的方式展开可以得到不同的平面展开图.
1.一个正三棱锥的表面可以展开成如下图中的哪个平面图形
交流
答:图1.
2.下图所示的平面图形中,哪些能围成一个正方体
答:图1、图2、图3.
某灯具厂要制作一批灯具,设计师给出了如图1所示的灯具三视图的示意图,试按照三视图确定制作每个灯具所需材料的面积 ( 精确到 0. 1m2) .
分析: 在本题中,如果知道每个灯具的侧面积和底面积,就可知道制作每个灯具所需材料的总面积 . 因此,解决本题的思路是先由三视图判断出灯具的立体模型,然后再由立体模型画出它的一个平面展开图,从而计算出它的总面积 .
图1
典型例题
解:由图1可知,灯具是正三棱柱形状 . 如图2所示,其上、下底是相同的等边三角形,三个侧面是相同的矩形,而且矩形的长为6m、宽为 4 m,等边三角形的边长为6m,所以可得到这个正三棱柱灯具的一个平面展开图,如图。
图1
图2
由展开图可知,制作一个灯具所需材料的面积为
( × 6 × 6sin60°) × 2 + ( 4 × 6 ) × 3
≈ 103. 2 ( m2 ).
答:制作每个灯具所需材料的面积约为 103. 2 m2 .
解:(1)侧面数(4个)≠底面边数(3条),不能围成棱柱.
(2)两底面在侧面展开图的同一端,不在两端,所以也不能围成棱柱.
(3)可以折成棱柱。
1.下面图形经过折叠能否围成棱柱?
基础检测
2.下面几个图形是一些常见几何体的展开图,你能正确说出这些几何体的名字么?
圆锥 四棱锥 长方体 三棱柱
三棱锥 三棱柱 正方体 圆柱
3.如图,上面的图形分别是下面哪个立体图形展开的形状?把它们用线连起来.
4.下图是一些立体图形的展开图,用它们能围成怎样的立体图形?
正方体
圆柱
三棱柱
圆锥
一展身手
1.右图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( )。
A. B. C. D.
B
2.下图是一个正方体的平面展开图,如果使字母 A 出现在顶面,那么它的底面应该出现什么字母?
答:底面是F。
A
N
M
L
K
J
I
H
G
F
E
D
C
B
3.把左图中长方体的表面展开图,折叠成一个长方体,那么与字母 J重合的点是哪几个?
答:与J重合的点有:H , N
挑战自我
A
1
-4
3
-
2
1.下图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,求x的值.
A
1
-4
3
-
2
3x+2
解:依题意得,正方体的左面为-4,右面为3x+2,
即3x+2=-4,
解得x=-2.
课堂小结
比例基本几何体的平面展开图
1.常见几何体的展开图;
2.将展开图折叠成几何体。
主讲:
感谢聆听
京改版九年级下册
