专题05概率初步(考点串讲,3大考点16大题型突破3大易错剖析) 课件(共40张PPT)
文档属性
| 名称 | 专题05概率初步(考点串讲,3大考点16大题型突破3大易错剖析) 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 15:08:34 | ||
图片预览




文档简介
(共40张PPT)
九年级数学上学期·期末复习大串讲
专题05 概率初步
人教版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
三大常考点:知识梳理
十六大题型典例剖析
三大易错易混经典例题
精选3道期末真题对应考点练
目
录
1
0
0
1
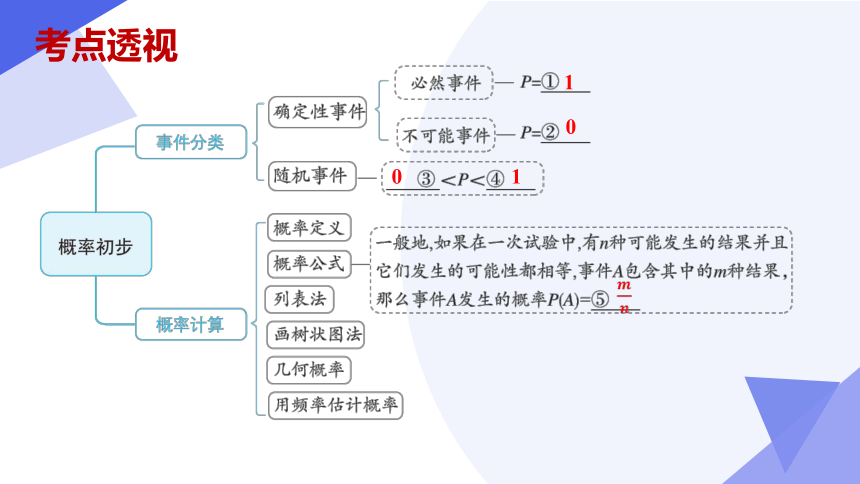
考点透视
考点1 事件类型的判定
1. [2023衡水模拟]下列事件中,属于确定性事件的是( D )
①抛出的篮球会下落;②从装有黑球、白球的袋中摸出红球;
③14人中至少有2人是同月出生;④买一张彩票,中1 000万大奖.
D
A. ①② B. ①③ C. ②④ D. ①②③
2. 下列事件中,属于不可能事件的是( D )
A. 逛书店遇到同学
B. 射击一次,命中靶心
C. 掷一次骰子,向上一面点数大于0
D. 任意画一个三角形,其内角和是360°
D
3. [2023江苏二模]下列说法正确的是( A )
A. 从一副扑克牌中任意抽取1张,抽到“A”是随机事件
B. 了解一批电视机的使用寿命适合采用普查
C. 要反映一周内每天气温的变化情况适宜采用扇形统计图
D. 抛掷一枚质地均匀的硬币,正面朝上是必然事件
A
考点2 求事件的概率
4. 有4条线段,长度分别为3 cm,4 cm,5 cm,6 cm,从中任取3条,能构成直角三角形的概率是( C )
A. B. C. D.
C
5. 在一个不透明的口袋中,有3个红球、1个白球,它们除颜色不同外其他完全相同,现从口袋中随机摸出一个球,记下颜色后不放回,再随机摸出一个球,则两次都摸到红球的概率是 .
6. 从-2,1,3中随机取一个数记为 a ,再从-1,0,2中随机取一个数记为 b ,则使一次函数 y = ax + b 的图象不经过第四象限的概率是 .
7. 如图,点 A 在☉ O 上,∠ BAC =60°,以 A 为圆心, AB 长为半径的扇形 ABC 内接于☉ O . 某人向☉ O 区域内任意投掷一枚飞镖,则飞镖恰好落在扇形 ABC 内的概率为 .
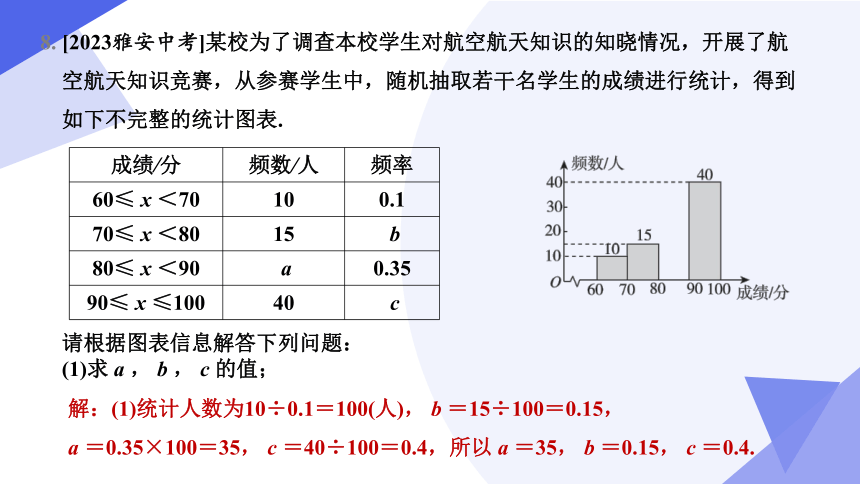
8. [2023雅安中考]某校为了调查本校学生对航空航天知识的知晓情况,开展了航空航天知识竞赛,从参赛学生中,随机抽取若干名学生的成绩进行统计,得到如下不完整的统计图表.
请根据图表信息解答下列问题:
(1)求 a , b , c 的值;
成绩/分 频数/人 频率
60≤ x <70 10 0.1
70≤ x <80 15 b
80≤ x <90 a 0.35
90≤ x ≤100 40 c
解:(1)统计人数为10÷0.1=100(人), b =15÷100=0.15,
a =0.35×100=35, c =40÷100=0.4,所以 a =35, b =0.15, c =0.4.
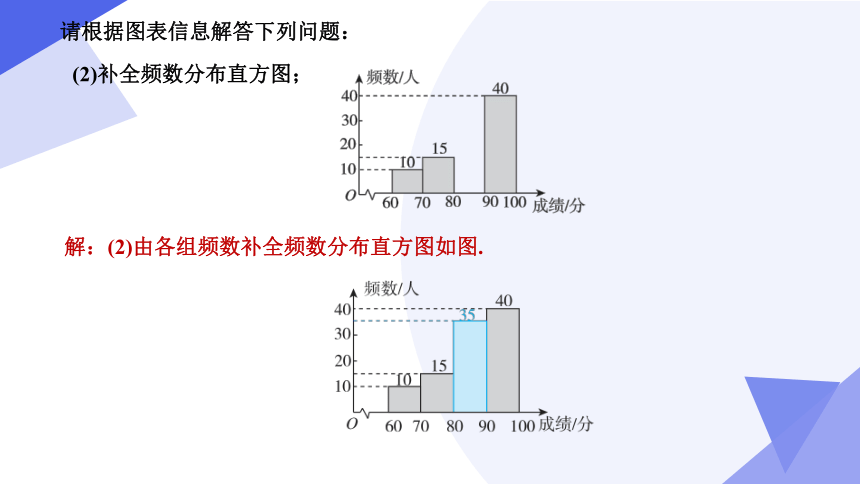
(2)补全频数分布直方图;
请根据图表信息解答下列问题:
解:(2)由各组频数补全频数分布直方图如图.
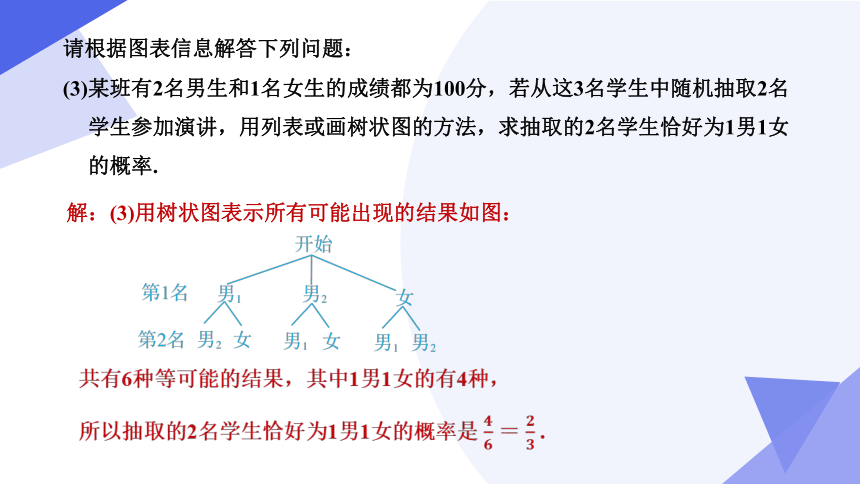
(3)某班有2名男生和1名女生的成绩都为100分,若从这3名学生中随机抽取2名学生参加演讲,用列表或画树状图的方法,求抽取的2名学生恰好为1男1女的概率.
请根据图表信息解答下列问题:
解:(3)用树状图表示所有可能出现的结果如图:
共有6种等可能的结果,其中1男1女的有4种,
所以抽取的2名学生恰好为1男1女的概率是 = .
考点3 用频率估计概率
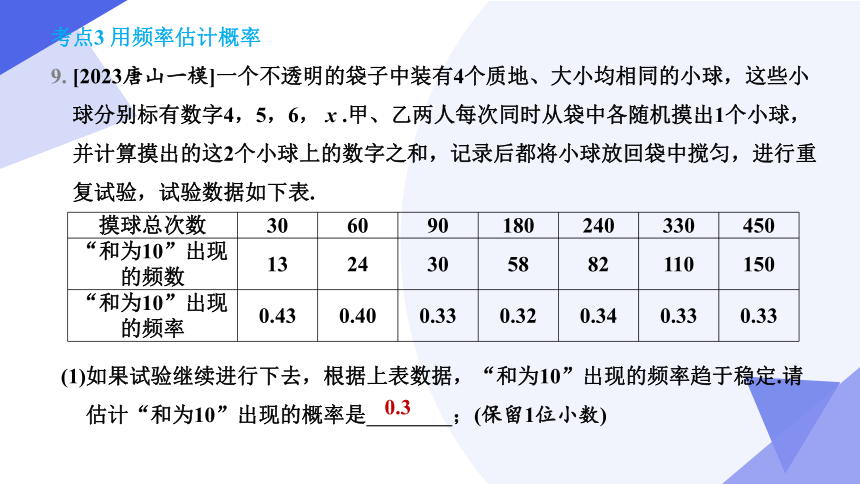
9. [2023唐山一模]一个不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字4,5,6, x .甲、乙两人每次同时从袋中各随机摸出1个小球,并计算摸出的这2个小球上的数字之和,记录后都将小球放回袋中搅匀,进行重复试验,试验数据如下表.
摸球总次数 30 60 90 180 240 330 450
“和为10”出现的频数 13 24 30 58 82 110 150
“和为10”出现的频率 0.43 0.40 0.33 0.32 0.34 0.33 0.33
(1)如果试验继续进行下去,根据上表数据,“和为10”出现的频率趋于稳定.请估计“和为10”出现的概率是 ;(保留1位小数)
0.3
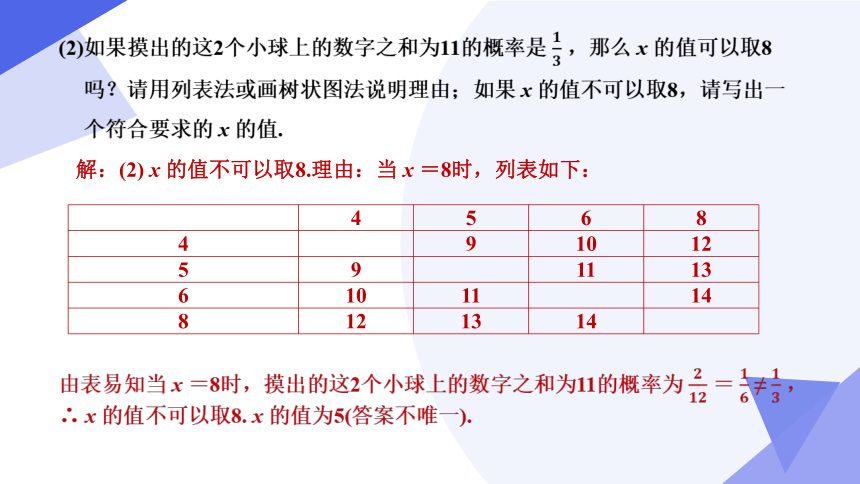
解:(2) x 的值不可以取8.理由:当 x =8时,列表如下:
4 5 6 8
4 9 10 12
5 9 11 13
6 10 11 14
8 12 13 14
由表易知当 x =8时,摸出的这2个小球上的数字之和为11的概率为 = ≠ ,∴ x 的值不可以取8. x 的值为5(答案不唯一).
(2)如果摸出的这2个小球上的数字之和为11的概率是 ,那么 x 的值可以取8吗?请用列表法或画树状图法说明理由;如果 x 的值不可以取8,请写出一个符合要求的 x 的值.
类型 1 利用概率判断摸球游戏的公平性
1. 一个不透明口袋中有三个小球,一个标有字母A,另外两个都标有字母B,除所标字母不同外,其他完全相同.小颖和小刚做摸球游戏,小颖从中随机摸出一个小球,记下字母后放回并搅匀,小刚再随机摸出一个小球,两次摸出的小球所标字母相同则小颖赢,所标字母不同则小刚赢.
(1)用画树状图或列表的方法,求小颖赢的概率.
专项突破1 利用概率判断游戏规则的公平性
解:(1)画树状图如图.
共有9种等可能的结果,其中两次摸出的小球所标字母相同的结果有5种,
所以 P (小颖赢)= .
(2)请问这个游戏规则对双方公平吗?说明理由.
解:(2)不公平.理由如下:∵ P (小颖赢)= ,
∴ P (小刚赢)=1- = .∵ ≠ ,
∴这个游戏规则对双方不公平.
类型 2 利用概率判断转盘游戏的公平性
2. [2023邢台期中]如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别标有数字1,2,3,4,转动转盘A,B各一次,当转盘停止转动时,将指针指向扇形中的两个数字相加(当指针落在两扇形的交线上时,重新转动转盘).
(1)用树状图列出所有可能出现的结果.
解:(1) 画树状图如图.
两个数字的和分别为2,3,4,5,3,4,5,6,4,5,6,7,则共有12种等可能的结果.
(2)若规定指针指向扇形中的两个数字的和为5时甲赢,和为4时乙赢,和为其他数字时,甲、乙平局.请问这个游戏对甲、乙两人是否公平?
解:(2)∵两个数字的和为5的结果有3种,两个数字的和为4的结果有3种,
∴两个数字的和为5的概率是 = ,两个数字的和为4的概率是 = .
∵ = ,∴这个游戏对甲、乙两人是公平的.
类型 3 利用概率判断抽卡片游戏的公平性
3. [2023昆明模拟]安安和桃桃两名同学玩抽卡游戏,游戏规则如下:在大小和形状完全相同的4张卡片上分别标上数字2,4,4,5,将这4张卡片放入一个不透明盒子中搅匀,参与者每次从中随机抽取一张卡片,记录数字,然后将卡片放回搅匀.安安和桃桃各抽取卡片一次,若取出的两张卡片数字之和为2的倍数,则安安胜,否则桃桃胜.
(1)请你用列表或画树状图的方法分析说明此游戏是否公平?
解:(1)根据题意,列表如下.
2 4 4 5
2 4 6 6 7
4 6 8 8 9
4 6 8 8 9
5 7 9 9 10
共有16种等可能的情况,其中两张卡片数字之和为2的倍数的情况有10种.
∴ P (安安获胜)= = .∴ P (桃桃获胜)=1- = .
∵ ≠ ,∴此游戏不公平.
(2)请你基于(1)中得到的数据,设计出一种公平的游戏规则.(列出一种即可)
解:(2)在大小和形状完全相同的4张卡片上分别标上数字2,4,4,5,将这4张卡片放入一个不透明盒子中搅匀,参与者每次从中随机抽取一张卡片,记录数字不放回.安安和桃桃各抽取卡片一次,若取出的两张卡片数字之和为2的倍数,则安安胜,否则桃桃胜.
应用 1 概率在方程和不等式中的应用
1. 小强同学从-1,0,1,2,3,4这六个数中任选一个数,所选的数满足不等式
x +1<2的概率是( C )
A. B. C. D.
C
专项突破2 概率与其他知识的综合应用
2. [2024温州月考]若 a 是从“-1,0,1,2”这四个数中任取的一个数,则关于 x 的方程( a -1) x2+ x -3=0为一元二次方程的概率是( A )
A
A. B. C. D. 1
3. [2023成都模拟]从-3,-2,-1,0,1,2,3这7个数中任意选择一个数作为 a 的值,则使关于 y 的分式方程 + =-1有非负整数解的概率为 .
点拨:解方程 + =-1,得 y = = +1.
∵ y 为非负整数,∴ a ≥-2且 a 为偶数.∴ a =-2或0或2.
但当 a =2时, y =2,它是分式方程的增根,故 a =2不符合题意,
∴ a =-2或0.
∴使关于 y 的分式方程 + =-1有非负整数解的概率为 .
应用 2 概率在函数中的应用
类型 1 不放回事件
4. [2023重庆八中月考]不透明的袋子里装有除标号外完全一样的三个小球,小球上分别标有-3,1,4这三个数字,从袋子中随机摸取一个小球,记标号为 m 后不放回,将小球摇匀后,再从袋子里剩下的小球中随机摸取一个小球,记标号为 n ,则 m , n 使得二次函数 y = mx2+ n 的图象同时经过四个象限的概率为 .
点思路:从袋子中随机摸取一个小球,记标号为 m 后不放回,将小球摇匀后,再随机摸取一个小球,记标号为 n ,则共有6个数组,使得二次函数 y = mx2+ n 的图象同时经过四个象限的数组有(-3,1),(-3,4),(1,-3),(4,-3),共4个.
类型 2 放回事件
5. [2024湖州期末]有三个质地、大小都相同的小球分别标上数字2,-2,3后放入一个不透明的口袋搅匀,任意摸出一个小球,记下数字 a 后,放回口袋中搅匀,再任意摸出一个小球,又记下数字 b .这样就得到一个点的坐标( a , b ).
(1)求这个点( a , b )恰好在函数 y =- x 的图象上的概率(请用“画树状图”或“列表”的方法给出分析过程,并求出结果).
解:(1)列表如下.
b a 2 -2 3
2 (2,2) (2,-2) (2,3)
-2 (-2,2) (-2,-2) (-2,3)
3 (3,2) (3,-2) (3,3)
∴共有9种等可能的结果,其中符合要求的结果有2种.
∴ P (点在函数 y =- x 的图象上)= .
(2)如果再往口袋中增加 n ( n ≥1)个标上数字2的小球,按照同样的操作过程,所得到的点( a , b )恰好在函数 y =- x 的图象上的概率是 (请用含 n 的代数式直接写出结果).
应用 3 概率在几何中的应用
6. 如图,已知正六边形 ABCDEF 内接于半径为 r 的☉ O ,随机地往☉ O 内投一粒米,落在正六边形内的概率为( A )
A. B.
C. D. 以上答案都不对
A
A
7. [2023保定二模]“七巧板”是古代中国劳动人民的发明,被誉为“东方魔板”.如图①是由七巧板组成的正方形,如图②是用该七巧板拼成的“和平鸽”图形,现将一个飞镖随机投掷到该图形上,则飞镖落在和平鸽头部(阴影部分)
的概率是( C )
A. B. C. D.
C
类型 1 概率跨语文学科
1. 下列成语或词语所反映的事件中,发生的可能性最小的是( A )
A. 刻舟求剑 B. 旭日东升
C. 夕阳西下 D. 瓜熟蒂落
A
专项突破3 概率中的跨学科试题
2. [2023赣州模拟]欧阳修的《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,卖油翁的技艺让人叹为观止.若铜钱是直径为3 cm的圆面,中间有边长为1 cm的正方形孔.现随机向铜钱上滴一滴油(油滴的大小忽略不计),那么油滴落入孔中的概率为 .
类型 2 概率跨英语学科
3. 甲口袋中装有2个相同的小球,它们分别写有字母A和B,乙口袋中装有2个相同的小球,它们分别写有字母C和D,丙口袋中装有2个相同的小球,它们分别写有字母H和I. 从三个口袋中各随机摸出1个小球,3个小球上恰好有1个元
音字母(本题中A,I是元音字母;B,C,D,H是辅音字母)的概率是( C )
C
A. B. C. D.
类型 3 概率跨物理学科
4. [2023太原模拟]如图所示,电路图上有3个开关S1,S2,S3 和2个小灯泡L1,L2,同时闭合开关S1,S2,S3可以使小灯泡L1,L2发光.对于“小灯泡发光”这个事件,下列结论错误的是( C )
C
A. 闭合开关S1,S2,S3中的1个,灯泡L1发光是不可能事件
B. 闭合开关S1,S2,S3中的2个,灯泡L2发光是随机事件
C. 闭合开关S1,S2,S3中的2个,灯泡L1发光是必然事件
D. 闭合开关S1,S2,S3中的2个,灯泡L1,L2发光的概率相同
5. [2023成都模拟]在如图所示的电路图中,当随机闭合开关S1,S2,S3,S4中的两个时,能够让灯泡发光的概率为 .
类型 4 概率跨化学学科
6. [2024黔东南州月考]有4个外观完全相同的密封且不透明试剂瓶,分别装有稀硫酸、稀盐酸、氯化钠、碳酸钠四种溶液.小星从这4个试剂瓶中任意抽取2个,则抽到的2个都是酸性溶液(稀硫酸溶液、稀盐酸溶液)的概率是 .
类型5概率跨地理学科
7. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票(如图)中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张,不放回,再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是( C )
C
A. B. C. D.
类型 6 概率跨体育学科
8. [2023德州二模]某学校男生体育测试从立定跳远、引体向上、100米跑、1 000米跑四个项目中随机抽取两项进行测试,恰好抽到立定跳远和100米跑的概率为 .
类型 7 概率跨生物学科
9. 人类的性别是由一对性染色体(X,Y)决定的,当性染色体为XX时,是女性;当性染色体为XY时,是男性.如图为一对夫妻的性染色体遗传图谱,如果这位女士怀上了一个小孩,该小孩为女孩的概率是 .
类型 8 概率跨音乐学科
10. [2023济南三模]“宫商角徵羽”是中国古乐的五个基本音阶(相当于西乐的1,2,3,5,6).现有一款“一起听古音”的音乐玩具,如图,音乐小球从 A 处沿轨道进入小洞就可以发出相应的声音,且小球每次进入每个小洞的可能性大小相等.现有一个音乐小球从 A 处先后两次进入小洞,先发出“商”音,再发出“羽”音的概率是( D )
D
A. B. C. D.
类型 9 概率跨美术学科
11. 素描是写实绘画的基础,常说的素描五大调子是指高光、中间色、明暗交界线、反光、投影.美术老师想从这五大调子中先选择两大调子让学生重点练习,则正好选中高光与中间色的概率为 .
类型 10 概率跨历史学科
12. 公元前138年张骞出使西域,自长安出发,经匈奴,西行至大宛,经康居,抵达大月氏,再至大夏,最后于公元前126年返回汉朝.张骞出使西域后汉夷文化交往频繁,中原文明通过“丝绸之路”迅速向四周传播.根据古今地图对比,南南同学发现丝绸之路途经现代西安,吐鲁番,喀什等地.
(1)南南爸爸想趁暑假一家人一起出游,若只能去一个地方游览,且选择三个地方的概率相等,那么南南从西安,吐鲁番,喀什三个城市中选择西安的概率是 .
(2)若时间充足,南南一家决定以上三个城市都去一趟,求南南一家最后一站去喀什的概率.
解:南南一家游览的顺序有西安,吐鲁番,喀什;西安,喀什,吐鲁番;喀什,吐鲁番,西安;喀什,西安,吐鲁番;吐鲁番,喀什,西安;吐鲁番,西安,喀什这6种等可能的结果,其中南南一家最后一站去喀什的结果有2种,所以南南一家最后一站去喀什的概率为 = .
易混易错
C
1. [2023青岛期末]下列说法正确的有( A )
(1)任意取两个整数,它们的和是整数是必然事件;
(2)一副去掉大小王的普通扑克牌(52张,四种花色)洗匀后,从中任抽一张牌,花色是梅花是随机事件;
(3)不透明袋子中有1个红球和4个白球,每个球除颜色外都相同,从中任取一球是白球的可能性大;
A
(4)任意掷一枚质地均匀的骰子,掷出的点数不超过6是必然事件.
A. 4个 B. 3个
C. 2个 D. 1个
押题预测
2. [2024宿迁期末]如图,等边三角形 ABC 是由9个大小相等的等边三角形构成,随机地往△ ABC 内投一粒米,落在阴影区域的概率为 .
3. [2023·青岛二模 新考向·数学文化]圆周率π是无限不循环小数.历史上,中国数学家祖冲之、刘徽,外国数学家韦达、欧拉等都对π有过深入的研究.目前,超级计算机已计算出π的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)从π的小数部分随机取出一个数字,该数字是偶数的概率为 ;
(2)某校进行校园文化建设,拟从以上4位数学家的画像中随机选用2幅.请用列表或画树状图的方法,求选中的画像正好是一中一外两位数学家的概率.
解:将祖冲之、刘徽、韦达、欧拉四位数学家分别记作甲、乙、丙、丁,列表如下.
甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
由表可知,共有12种等可能的结果,其中画像正好是一中一外两位数学家的结果有8种,∴其中画像正好是一中一外两位数学家的概率为 = .
九年级数学上学期·期末复习大串讲
专题05 概率初步
人教版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
三大常考点:知识梳理
十六大题型典例剖析
三大易错易混经典例题
精选3道期末真题对应考点练
目
录
1
0
0
1
考点透视
考点1 事件类型的判定
1. [2023衡水模拟]下列事件中,属于确定性事件的是( D )
①抛出的篮球会下落;②从装有黑球、白球的袋中摸出红球;
③14人中至少有2人是同月出生;④买一张彩票,中1 000万大奖.
D
A. ①② B. ①③ C. ②④ D. ①②③
2. 下列事件中,属于不可能事件的是( D )
A. 逛书店遇到同学
B. 射击一次,命中靶心
C. 掷一次骰子,向上一面点数大于0
D. 任意画一个三角形,其内角和是360°
D
3. [2023江苏二模]下列说法正确的是( A )
A. 从一副扑克牌中任意抽取1张,抽到“A”是随机事件
B. 了解一批电视机的使用寿命适合采用普查
C. 要反映一周内每天气温的变化情况适宜采用扇形统计图
D. 抛掷一枚质地均匀的硬币,正面朝上是必然事件
A
考点2 求事件的概率
4. 有4条线段,长度分别为3 cm,4 cm,5 cm,6 cm,从中任取3条,能构成直角三角形的概率是( C )
A. B. C. D.
C
5. 在一个不透明的口袋中,有3个红球、1个白球,它们除颜色不同外其他完全相同,现从口袋中随机摸出一个球,记下颜色后不放回,再随机摸出一个球,则两次都摸到红球的概率是 .
6. 从-2,1,3中随机取一个数记为 a ,再从-1,0,2中随机取一个数记为 b ,则使一次函数 y = ax + b 的图象不经过第四象限的概率是 .
7. 如图,点 A 在☉ O 上,∠ BAC =60°,以 A 为圆心, AB 长为半径的扇形 ABC 内接于☉ O . 某人向☉ O 区域内任意投掷一枚飞镖,则飞镖恰好落在扇形 ABC 内的概率为 .
8. [2023雅安中考]某校为了调查本校学生对航空航天知识的知晓情况,开展了航空航天知识竞赛,从参赛学生中,随机抽取若干名学生的成绩进行统计,得到如下不完整的统计图表.
请根据图表信息解答下列问题:
(1)求 a , b , c 的值;
成绩/分 频数/人 频率
60≤ x <70 10 0.1
70≤ x <80 15 b
80≤ x <90 a 0.35
90≤ x ≤100 40 c
解:(1)统计人数为10÷0.1=100(人), b =15÷100=0.15,
a =0.35×100=35, c =40÷100=0.4,所以 a =35, b =0.15, c =0.4.
(2)补全频数分布直方图;
请根据图表信息解答下列问题:
解:(2)由各组频数补全频数分布直方图如图.
(3)某班有2名男生和1名女生的成绩都为100分,若从这3名学生中随机抽取2名学生参加演讲,用列表或画树状图的方法,求抽取的2名学生恰好为1男1女的概率.
请根据图表信息解答下列问题:
解:(3)用树状图表示所有可能出现的结果如图:
共有6种等可能的结果,其中1男1女的有4种,
所以抽取的2名学生恰好为1男1女的概率是 = .
考点3 用频率估计概率
9. [2023唐山一模]一个不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字4,5,6, x .甲、乙两人每次同时从袋中各随机摸出1个小球,并计算摸出的这2个小球上的数字之和,记录后都将小球放回袋中搅匀,进行重复试验,试验数据如下表.
摸球总次数 30 60 90 180 240 330 450
“和为10”出现的频数 13 24 30 58 82 110 150
“和为10”出现的频率 0.43 0.40 0.33 0.32 0.34 0.33 0.33
(1)如果试验继续进行下去,根据上表数据,“和为10”出现的频率趋于稳定.请估计“和为10”出现的概率是 ;(保留1位小数)
0.3
解:(2) x 的值不可以取8.理由:当 x =8时,列表如下:
4 5 6 8
4 9 10 12
5 9 11 13
6 10 11 14
8 12 13 14
由表易知当 x =8时,摸出的这2个小球上的数字之和为11的概率为 = ≠ ,∴ x 的值不可以取8. x 的值为5(答案不唯一).
(2)如果摸出的这2个小球上的数字之和为11的概率是 ,那么 x 的值可以取8吗?请用列表法或画树状图法说明理由;如果 x 的值不可以取8,请写出一个符合要求的 x 的值.
类型 1 利用概率判断摸球游戏的公平性
1. 一个不透明口袋中有三个小球,一个标有字母A,另外两个都标有字母B,除所标字母不同外,其他完全相同.小颖和小刚做摸球游戏,小颖从中随机摸出一个小球,记下字母后放回并搅匀,小刚再随机摸出一个小球,两次摸出的小球所标字母相同则小颖赢,所标字母不同则小刚赢.
(1)用画树状图或列表的方法,求小颖赢的概率.
专项突破1 利用概率判断游戏规则的公平性
解:(1)画树状图如图.
共有9种等可能的结果,其中两次摸出的小球所标字母相同的结果有5种,
所以 P (小颖赢)= .
(2)请问这个游戏规则对双方公平吗?说明理由.
解:(2)不公平.理由如下:∵ P (小颖赢)= ,
∴ P (小刚赢)=1- = .∵ ≠ ,
∴这个游戏规则对双方不公平.
类型 2 利用概率判断转盘游戏的公平性
2. [2023邢台期中]如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别标有数字1,2,3,4,转动转盘A,B各一次,当转盘停止转动时,将指针指向扇形中的两个数字相加(当指针落在两扇形的交线上时,重新转动转盘).
(1)用树状图列出所有可能出现的结果.
解:(1) 画树状图如图.
两个数字的和分别为2,3,4,5,3,4,5,6,4,5,6,7,则共有12种等可能的结果.
(2)若规定指针指向扇形中的两个数字的和为5时甲赢,和为4时乙赢,和为其他数字时,甲、乙平局.请问这个游戏对甲、乙两人是否公平?
解:(2)∵两个数字的和为5的结果有3种,两个数字的和为4的结果有3种,
∴两个数字的和为5的概率是 = ,两个数字的和为4的概率是 = .
∵ = ,∴这个游戏对甲、乙两人是公平的.
类型 3 利用概率判断抽卡片游戏的公平性
3. [2023昆明模拟]安安和桃桃两名同学玩抽卡游戏,游戏规则如下:在大小和形状完全相同的4张卡片上分别标上数字2,4,4,5,将这4张卡片放入一个不透明盒子中搅匀,参与者每次从中随机抽取一张卡片,记录数字,然后将卡片放回搅匀.安安和桃桃各抽取卡片一次,若取出的两张卡片数字之和为2的倍数,则安安胜,否则桃桃胜.
(1)请你用列表或画树状图的方法分析说明此游戏是否公平?
解:(1)根据题意,列表如下.
2 4 4 5
2 4 6 6 7
4 6 8 8 9
4 6 8 8 9
5 7 9 9 10
共有16种等可能的情况,其中两张卡片数字之和为2的倍数的情况有10种.
∴ P (安安获胜)= = .∴ P (桃桃获胜)=1- = .
∵ ≠ ,∴此游戏不公平.
(2)请你基于(1)中得到的数据,设计出一种公平的游戏规则.(列出一种即可)
解:(2)在大小和形状完全相同的4张卡片上分别标上数字2,4,4,5,将这4张卡片放入一个不透明盒子中搅匀,参与者每次从中随机抽取一张卡片,记录数字不放回.安安和桃桃各抽取卡片一次,若取出的两张卡片数字之和为2的倍数,则安安胜,否则桃桃胜.
应用 1 概率在方程和不等式中的应用
1. 小强同学从-1,0,1,2,3,4这六个数中任选一个数,所选的数满足不等式
x +1<2的概率是( C )
A. B. C. D.
C
专项突破2 概率与其他知识的综合应用
2. [2024温州月考]若 a 是从“-1,0,1,2”这四个数中任取的一个数,则关于 x 的方程( a -1) x2+ x -3=0为一元二次方程的概率是( A )
A
A. B. C. D. 1
3. [2023成都模拟]从-3,-2,-1,0,1,2,3这7个数中任意选择一个数作为 a 的值,则使关于 y 的分式方程 + =-1有非负整数解的概率为 .
点拨:解方程 + =-1,得 y = = +1.
∵ y 为非负整数,∴ a ≥-2且 a 为偶数.∴ a =-2或0或2.
但当 a =2时, y =2,它是分式方程的增根,故 a =2不符合题意,
∴ a =-2或0.
∴使关于 y 的分式方程 + =-1有非负整数解的概率为 .
应用 2 概率在函数中的应用
类型 1 不放回事件
4. [2023重庆八中月考]不透明的袋子里装有除标号外完全一样的三个小球,小球上分别标有-3,1,4这三个数字,从袋子中随机摸取一个小球,记标号为 m 后不放回,将小球摇匀后,再从袋子里剩下的小球中随机摸取一个小球,记标号为 n ,则 m , n 使得二次函数 y = mx2+ n 的图象同时经过四个象限的概率为 .
点思路:从袋子中随机摸取一个小球,记标号为 m 后不放回,将小球摇匀后,再随机摸取一个小球,记标号为 n ,则共有6个数组,使得二次函数 y = mx2+ n 的图象同时经过四个象限的数组有(-3,1),(-3,4),(1,-3),(4,-3),共4个.
类型 2 放回事件
5. [2024湖州期末]有三个质地、大小都相同的小球分别标上数字2,-2,3后放入一个不透明的口袋搅匀,任意摸出一个小球,记下数字 a 后,放回口袋中搅匀,再任意摸出一个小球,又记下数字 b .这样就得到一个点的坐标( a , b ).
(1)求这个点( a , b )恰好在函数 y =- x 的图象上的概率(请用“画树状图”或“列表”的方法给出分析过程,并求出结果).
解:(1)列表如下.
b a 2 -2 3
2 (2,2) (2,-2) (2,3)
-2 (-2,2) (-2,-2) (-2,3)
3 (3,2) (3,-2) (3,3)
∴共有9种等可能的结果,其中符合要求的结果有2种.
∴ P (点在函数 y =- x 的图象上)= .
(2)如果再往口袋中增加 n ( n ≥1)个标上数字2的小球,按照同样的操作过程,所得到的点( a , b )恰好在函数 y =- x 的图象上的概率是 (请用含 n 的代数式直接写出结果).
应用 3 概率在几何中的应用
6. 如图,已知正六边形 ABCDEF 内接于半径为 r 的☉ O ,随机地往☉ O 内投一粒米,落在正六边形内的概率为( A )
A. B.
C. D. 以上答案都不对
A
A
7. [2023保定二模]“七巧板”是古代中国劳动人民的发明,被誉为“东方魔板”.如图①是由七巧板组成的正方形,如图②是用该七巧板拼成的“和平鸽”图形,现将一个飞镖随机投掷到该图形上,则飞镖落在和平鸽头部(阴影部分)
的概率是( C )
A. B. C. D.
C
类型 1 概率跨语文学科
1. 下列成语或词语所反映的事件中,发生的可能性最小的是( A )
A. 刻舟求剑 B. 旭日东升
C. 夕阳西下 D. 瓜熟蒂落
A
专项突破3 概率中的跨学科试题
2. [2023赣州模拟]欧阳修的《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,卖油翁的技艺让人叹为观止.若铜钱是直径为3 cm的圆面,中间有边长为1 cm的正方形孔.现随机向铜钱上滴一滴油(油滴的大小忽略不计),那么油滴落入孔中的概率为 .
类型 2 概率跨英语学科
3. 甲口袋中装有2个相同的小球,它们分别写有字母A和B,乙口袋中装有2个相同的小球,它们分别写有字母C和D,丙口袋中装有2个相同的小球,它们分别写有字母H和I. 从三个口袋中各随机摸出1个小球,3个小球上恰好有1个元
音字母(本题中A,I是元音字母;B,C,D,H是辅音字母)的概率是( C )
C
A. B. C. D.
类型 3 概率跨物理学科
4. [2023太原模拟]如图所示,电路图上有3个开关S1,S2,S3 和2个小灯泡L1,L2,同时闭合开关S1,S2,S3可以使小灯泡L1,L2发光.对于“小灯泡发光”这个事件,下列结论错误的是( C )
C
A. 闭合开关S1,S2,S3中的1个,灯泡L1发光是不可能事件
B. 闭合开关S1,S2,S3中的2个,灯泡L2发光是随机事件
C. 闭合开关S1,S2,S3中的2个,灯泡L1发光是必然事件
D. 闭合开关S1,S2,S3中的2个,灯泡L1,L2发光的概率相同
5. [2023成都模拟]在如图所示的电路图中,当随机闭合开关S1,S2,S3,S4中的两个时,能够让灯泡发光的概率为 .
类型 4 概率跨化学学科
6. [2024黔东南州月考]有4个外观完全相同的密封且不透明试剂瓶,分别装有稀硫酸、稀盐酸、氯化钠、碳酸钠四种溶液.小星从这4个试剂瓶中任意抽取2个,则抽到的2个都是酸性溶液(稀硫酸溶液、稀盐酸溶液)的概率是 .
类型5概率跨地理学科
7. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票(如图)中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张,不放回,再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是( C )
C
A. B. C. D.
类型 6 概率跨体育学科
8. [2023德州二模]某学校男生体育测试从立定跳远、引体向上、100米跑、1 000米跑四个项目中随机抽取两项进行测试,恰好抽到立定跳远和100米跑的概率为 .
类型 7 概率跨生物学科
9. 人类的性别是由一对性染色体(X,Y)决定的,当性染色体为XX时,是女性;当性染色体为XY时,是男性.如图为一对夫妻的性染色体遗传图谱,如果这位女士怀上了一个小孩,该小孩为女孩的概率是 .
类型 8 概率跨音乐学科
10. [2023济南三模]“宫商角徵羽”是中国古乐的五个基本音阶(相当于西乐的1,2,3,5,6).现有一款“一起听古音”的音乐玩具,如图,音乐小球从 A 处沿轨道进入小洞就可以发出相应的声音,且小球每次进入每个小洞的可能性大小相等.现有一个音乐小球从 A 处先后两次进入小洞,先发出“商”音,再发出“羽”音的概率是( D )
D
A. B. C. D.
类型 9 概率跨美术学科
11. 素描是写实绘画的基础,常说的素描五大调子是指高光、中间色、明暗交界线、反光、投影.美术老师想从这五大调子中先选择两大调子让学生重点练习,则正好选中高光与中间色的概率为 .
类型 10 概率跨历史学科
12. 公元前138年张骞出使西域,自长安出发,经匈奴,西行至大宛,经康居,抵达大月氏,再至大夏,最后于公元前126年返回汉朝.张骞出使西域后汉夷文化交往频繁,中原文明通过“丝绸之路”迅速向四周传播.根据古今地图对比,南南同学发现丝绸之路途经现代西安,吐鲁番,喀什等地.
(1)南南爸爸想趁暑假一家人一起出游,若只能去一个地方游览,且选择三个地方的概率相等,那么南南从西安,吐鲁番,喀什三个城市中选择西安的概率是 .
(2)若时间充足,南南一家决定以上三个城市都去一趟,求南南一家最后一站去喀什的概率.
解:南南一家游览的顺序有西安,吐鲁番,喀什;西安,喀什,吐鲁番;喀什,吐鲁番,西安;喀什,西安,吐鲁番;吐鲁番,喀什,西安;吐鲁番,西安,喀什这6种等可能的结果,其中南南一家最后一站去喀什的结果有2种,所以南南一家最后一站去喀什的概率为 = .
易混易错
C
1. [2023青岛期末]下列说法正确的有( A )
(1)任意取两个整数,它们的和是整数是必然事件;
(2)一副去掉大小王的普通扑克牌(52张,四种花色)洗匀后,从中任抽一张牌,花色是梅花是随机事件;
(3)不透明袋子中有1个红球和4个白球,每个球除颜色外都相同,从中任取一球是白球的可能性大;
A
(4)任意掷一枚质地均匀的骰子,掷出的点数不超过6是必然事件.
A. 4个 B. 3个
C. 2个 D. 1个
押题预测
2. [2024宿迁期末]如图,等边三角形 ABC 是由9个大小相等的等边三角形构成,随机地往△ ABC 内投一粒米,落在阴影区域的概率为 .
3. [2023·青岛二模 新考向·数学文化]圆周率π是无限不循环小数.历史上,中国数学家祖冲之、刘徽,外国数学家韦达、欧拉等都对π有过深入的研究.目前,超级计算机已计算出π的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0~9这10个数字出现的频率趋于稳定,接近相同.
(1)从π的小数部分随机取出一个数字,该数字是偶数的概率为 ;
(2)某校进行校园文化建设,拟从以上4位数学家的画像中随机选用2幅.请用列表或画树状图的方法,求选中的画像正好是一中一外两位数学家的概率.
解:将祖冲之、刘徽、韦达、欧拉四位数学家分别记作甲、乙、丙、丁,列表如下.
甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
由表可知,共有12种等可能的结果,其中画像正好是一中一外两位数学家的结果有8种,∴其中画像正好是一中一外两位数学家的概率为 = .
同课章节目录
