北师大八上5.3应用二元一次方程组--鸡兔同笼
文档属性
| 名称 | 北师大八上5.3应用二元一次方程组--鸡兔同笼 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-22 14:16:49 | ||
图片预览




文档简介
(共25张PPT)
第五章 二元一次方程组
5.3应用二元一次方程组--鸡兔同笼
北师大版 数学 八年级 上册
学习目标
1、能根据具体问题中的等量关系,列出二元一次方程组解决实际问题.
2、借助“鸡兔同笼”类型的练习,熟练应用二元一次方程组解决实际问题.
情景导入
探索新知
应用二元一次方程组解古算题
一
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题”雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
探索新知
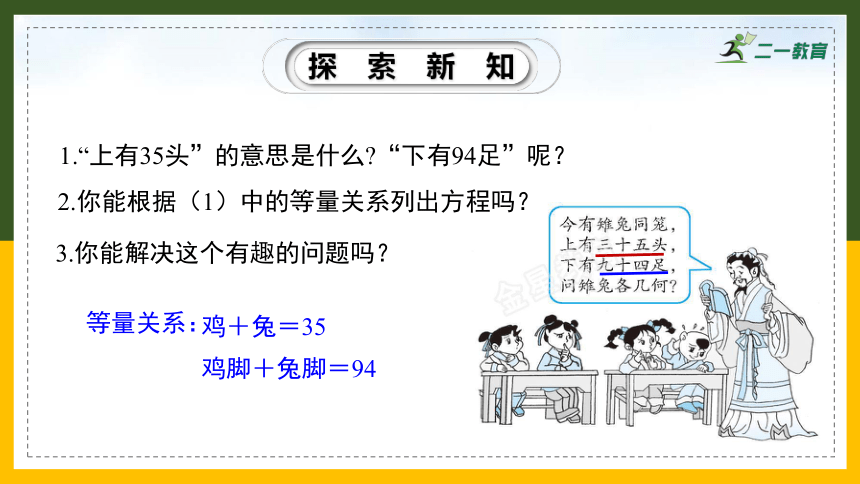
1.“上有35头”的意思是什么 “下有94足”呢?
2.你能根据(1)中的等量关系列出方程吗?
3.你能解决这个有趣的问题吗?
等量关系:
鸡+兔=35
鸡脚+兔脚=94
探索新知
解:设有鸡 x 只,则有兔(35-x)只.
由题意得:2x+4×(35-x)=94 .
解得x=23 .
∴ 35-x=12 .
答:有鸡23只,兔12只.
以前学习过的一元一次方程,能不能解决这一问题
总结归纳
探索新知
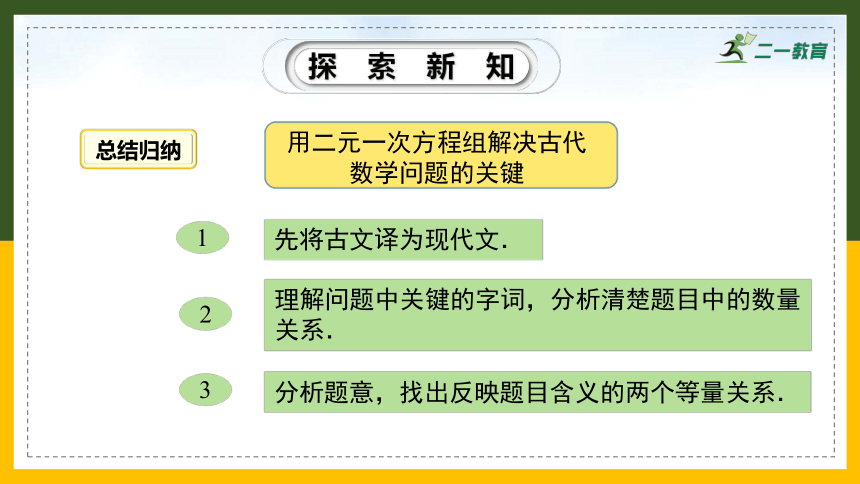
用二元一次方程组解决古代数学问题的关键
1
先将古文译为现代文.
理解问题中关键的字词,分析清楚题目中的数量关系.
分析题意,找出反映题目含义的两个等量关系.
2
3
探索新知
2x+4y=94
x+y=35
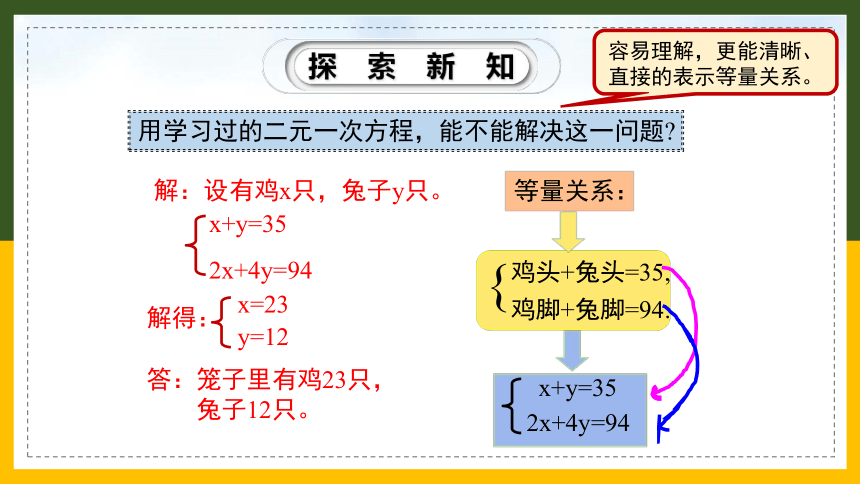
解:设有鸡x只,兔子y只。
答:笼子里有鸡23只,
兔子12只。
x=23
解得:
y=12
鸡头+兔头=35,
鸡脚+兔脚=94.
{
等量关系:
用学习过的二元一次方程,能不能解决这一问题
x+y=35
2x+4y=94
容易理解,更能清晰、直接的表示等量关系。
探索新知
总结归纳
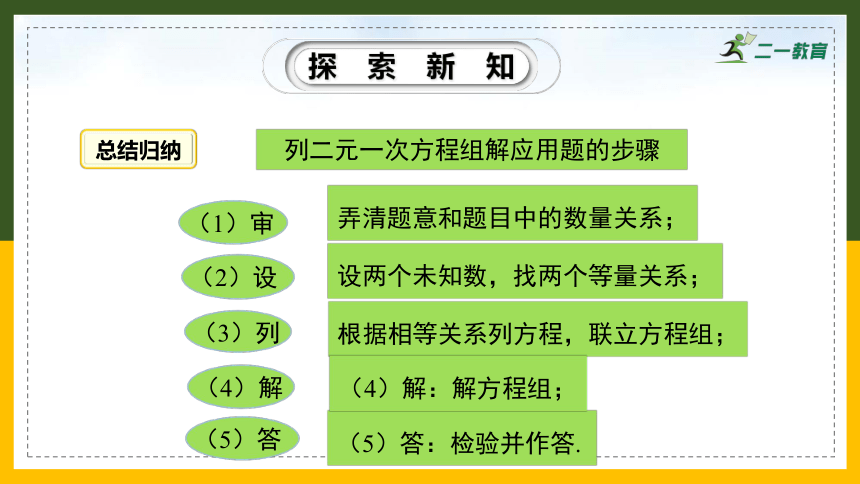
列二元一次方程组解应用题的步骤
(5)答:检验并作答.
弄清题意和题目中的数量关系;
设两个未知数,找两个等量关系;
根据相等关系列方程,联立方程组;
(4)解:解方程组;
(1)审
(2)设
(3)列
(4)解
(5)答
探索新知
例1.以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺.绳长,井深各几何
题目大意:用绳子测量水井的深度。如果将绳子折成三等份,一份绳长比井深多5尺;如果将绳子折成四等份,一份绳长比井深多1尺。绳长、井深各多少尺?
探索新知
绳长的 -5 =井深
绳长的 - 1 =井深
以井深为研究对
象,找等量关系
解:设绳长x尺,井深y尺.
井深
绳长
三等份
绳长
四等份
思路一 :
探索新知
思路一 :
解:设绳长x尺,井深y尺,
则由题意得
解得 x = 48
将x = 48代入① 得 y = 11
答:绳长48尺,井深11尺.
由①-②得
①
②
x - y =5
x - y =1
绳长的 - 井深 = 5
绳长的 - 井深 = 1
井深
绳三折
绳四折
探索新知
(井深+5)×3=绳长
(井深+1)×4=绳长
以绳长为研究对
象,找等量关系
井深
绳长
三等份
绳长
四等份
思路二 :
探索新知
思路二 :
井深
绳三折
绳四折
解:设绳长x尺,井深y尺,
则由题意得: 3 (y+5) = x
4 (y+1) = x
答:绳长48尺,井深11尺.
解得:
x = 48
y = 11
(井深+5)×3=绳长
(井深+1)×4=绳长
探索新知
例2:《九章算术》中记载:“今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?”
题目大意:5头牛、2只羊共价值10两“金”.2头牛、5只羊共价值8两“金”.则每头多少“金”、每只羊多少“金”?
探索新知
解:设每头牛值“金”x两,设每只羊值“金”y两.
由题意,得 解得
答:每头牛值“金” 两,每只羊值“金” 两.
当堂检测
1.某年级共有学生246人,其中男生人数 比女生人数 的2倍多2人,则
下面所列的方程组中符合题意的是( )
C
A. B.
C. D.
当堂检测
2.学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是 ,求两
种球各有多少个 若设篮球有 个,排球有 个,根据题意得方程组为
( )
D
A. B.
C. D.
当堂检测
3.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知3匹小马能拉1片瓦,1匹大马能拉3片瓦,求小马、大马各有多少匹.若设小马有x匹,大马有y匹,则下列方程组正确的是( )
A. B.
C. D.
C
当堂检测
4.某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队在12场比赛中得20分.设该队胜x场,负y场,则根据题意,列出关于x,y的二元一次方程组正确的是( )
A. B.
C. D.
D
当堂检测
5.某年级学生共有300人,其中男生人数y比女生人数x的2倍少2人,
根据题中的等量关系:
①某年级学生共有300人,则:_____________.
②男生人数y比女生人数x的2倍少2人,则:________.
x+y=300
2x=y+2
当堂检测
6.某校八年级10个班级师生举行“庆国庆——弘扬民族精神”文艺汇演比赛,每个班2个节目,分歌唱和朗诵两类.统计后发现歌唱类节目数比朗诵类节目数的2倍少4个,八年级师生表演的歌唱类和朗诵类节目各有多少个
解:设八年级师生表演的歌唱类节目有x个,朗诵类节目有y个.根据题意,得
解得
答:八年级师生表演的歌唱类节目有12个,朗诵类节目有8个.
当堂检测
7.某停车场的收费标准如下:中型汽车的停车费为15元/辆,小型汽车的停车费为8元/辆.现在停车场内停有30辆中、小型汽车,这些车共缴纳停车费324元,求中、小型汽车各有多少辆.
解:设中型汽车有x辆,小型汽车有y辆.
依题意得
解得
答:中型汽车有12辆,小型汽车有18辆.
列方程组解决问题
感谢收看
第五章 二元一次方程组
5.3应用二元一次方程组--鸡兔同笼
北师大版 数学 八年级 上册
学习目标
1、能根据具体问题中的等量关系,列出二元一次方程组解决实际问题.
2、借助“鸡兔同笼”类型的练习,熟练应用二元一次方程组解决实际问题.
情景导入
探索新知
应用二元一次方程组解古算题
一
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题”雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
探索新知
1.“上有35头”的意思是什么 “下有94足”呢?
2.你能根据(1)中的等量关系列出方程吗?
3.你能解决这个有趣的问题吗?
等量关系:
鸡+兔=35
鸡脚+兔脚=94
探索新知
解:设有鸡 x 只,则有兔(35-x)只.
由题意得:2x+4×(35-x)=94 .
解得x=23 .
∴ 35-x=12 .
答:有鸡23只,兔12只.
以前学习过的一元一次方程,能不能解决这一问题
总结归纳
探索新知
用二元一次方程组解决古代数学问题的关键
1
先将古文译为现代文.
理解问题中关键的字词,分析清楚题目中的数量关系.
分析题意,找出反映题目含义的两个等量关系.
2
3
探索新知
2x+4y=94
x+y=35
解:设有鸡x只,兔子y只。
答:笼子里有鸡23只,
兔子12只。
x=23
解得:
y=12
鸡头+兔头=35,
鸡脚+兔脚=94.
{
等量关系:
用学习过的二元一次方程,能不能解决这一问题
x+y=35
2x+4y=94
容易理解,更能清晰、直接的表示等量关系。
探索新知
总结归纳
列二元一次方程组解应用题的步骤
(5)答:检验并作答.
弄清题意和题目中的数量关系;
设两个未知数,找两个等量关系;
根据相等关系列方程,联立方程组;
(4)解:解方程组;
(1)审
(2)设
(3)列
(4)解
(5)答
探索新知
例1.以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺.绳长,井深各几何
题目大意:用绳子测量水井的深度。如果将绳子折成三等份,一份绳长比井深多5尺;如果将绳子折成四等份,一份绳长比井深多1尺。绳长、井深各多少尺?
探索新知
绳长的 -5 =井深
绳长的 - 1 =井深
以井深为研究对
象,找等量关系
解:设绳长x尺,井深y尺.
井深
绳长
三等份
绳长
四等份
思路一 :
探索新知
思路一 :
解:设绳长x尺,井深y尺,
则由题意得
解得 x = 48
将x = 48代入① 得 y = 11
答:绳长48尺,井深11尺.
由①-②得
①
②
x - y =5
x - y =1
绳长的 - 井深 = 5
绳长的 - 井深 = 1
井深
绳三折
绳四折
探索新知
(井深+5)×3=绳长
(井深+1)×4=绳长
以绳长为研究对
象,找等量关系
井深
绳长
三等份
绳长
四等份
思路二 :
探索新知
思路二 :
井深
绳三折
绳四折
解:设绳长x尺,井深y尺,
则由题意得: 3 (y+5) = x
4 (y+1) = x
答:绳长48尺,井深11尺.
解得:
x = 48
y = 11
(井深+5)×3=绳长
(井深+1)×4=绳长
探索新知
例2:《九章算术》中记载:“今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?”
题目大意:5头牛、2只羊共价值10两“金”.2头牛、5只羊共价值8两“金”.则每头多少“金”、每只羊多少“金”?
探索新知
解:设每头牛值“金”x两,设每只羊值“金”y两.
由题意,得 解得
答:每头牛值“金” 两,每只羊值“金” 两.
当堂检测
1.某年级共有学生246人,其中男生人数 比女生人数 的2倍多2人,则
下面所列的方程组中符合题意的是( )
C
A. B.
C. D.
当堂检测
2.学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是 ,求两
种球各有多少个 若设篮球有 个,排球有 个,根据题意得方程组为
( )
D
A. B.
C. D.
当堂检测
3.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知3匹小马能拉1片瓦,1匹大马能拉3片瓦,求小马、大马各有多少匹.若设小马有x匹,大马有y匹,则下列方程组正确的是( )
A. B.
C. D.
C
当堂检测
4.某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队在12场比赛中得20分.设该队胜x场,负y场,则根据题意,列出关于x,y的二元一次方程组正确的是( )
A. B.
C. D.
D
当堂检测
5.某年级学生共有300人,其中男生人数y比女生人数x的2倍少2人,
根据题中的等量关系:
①某年级学生共有300人,则:_____________.
②男生人数y比女生人数x的2倍少2人,则:________.
x+y=300
2x=y+2
当堂检测
6.某校八年级10个班级师生举行“庆国庆——弘扬民族精神”文艺汇演比赛,每个班2个节目,分歌唱和朗诵两类.统计后发现歌唱类节目数比朗诵类节目数的2倍少4个,八年级师生表演的歌唱类和朗诵类节目各有多少个
解:设八年级师生表演的歌唱类节目有x个,朗诵类节目有y个.根据题意,得
解得
答:八年级师生表演的歌唱类节目有12个,朗诵类节目有8个.
当堂检测
7.某停车场的收费标准如下:中型汽车的停车费为15元/辆,小型汽车的停车费为8元/辆.现在停车场内停有30辆中、小型汽车,这些车共缴纳停车费324元,求中、小型汽车各有多少辆.
解:设中型汽车有x辆,小型汽车有y辆.
依题意得
解得
答:中型汽车有12辆,小型汽车有18辆.
列方程组解决问题
感谢收看
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
