14.3.1因式分解---提公因式法 课件(共22张PPT)
文档属性
| 名称 | 14.3.1因式分解---提公因式法 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
人教版 八年级数学上
14.3.1因式分解---提公因式法
学习目标
1.理解因式分解的意义和概念及其与整式乘法的区别和联系.
(重点)
2.理解并掌握提公因式法并能熟练地运用提公因式法分解因式.(难点)
温故知新
2.填空:
1.说一说单项式乘以多项式的计算法则?
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
合作探究
请把下列多项式写成整式的乘积的形式:
像这样, 把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式.
因式分解与整式乘法有什么关系?
x2-1 (x+1)(x-1)
因式分解
整式乘法
是互为相反的变形,即:
小试牛刀
在下列等式中,从左到右的变形哪些是因式分解,不是的请说明理由.
①
②
③
④
⑤
⑥
am+bm+c=m(a+b)+c
24x2y=3x ·8xy
x2-1=(x+1)(x-1)
(2x+1)2=4x2+4x+1
x2+x=x2(1+ )
2x+4y+6z=2(x+2y+3z)
不是;最后不是积的运算
不是;因式分解的对象是多项式
不是;是整式乘法
不是;每个因式必须是整式
是
是
合作探究
pa+pb+pc
像上式,它的各项都有公共的因式P,我们把因式P叫做这个多项式各项的公因式.
公共的因式p
思考1: 观察下列多项式,它们有什么共同特点?
合作探究
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
( a+b+c )
可得pa+ pb +pc
p
=
由于 ( a+b+c )
=pa+ pb +pc
p
合作探究
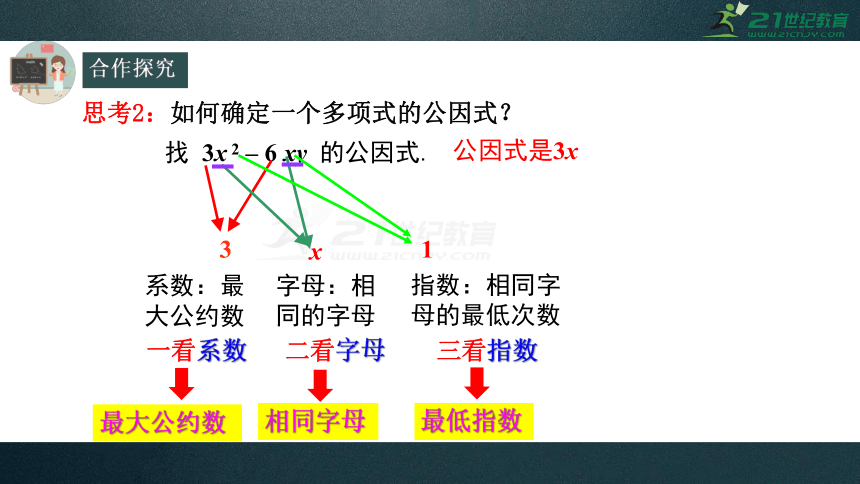
找 3x 2 – 6 xy 的公因式.
系数:最大公约数
3
字母:相同的字母
x
公因式是3x
指数:相同字母的最低次数
1
思考2:如何确定一个多项式的公因式?
一看系数 二看字母 三看指数
最大公约数
相同字母
最低指数
小试牛刀
下列各多项式的公因式是什么?
2
a
a2
2(m+n)
3mn
-2xy
(1)2x+6y
(2)ab-2ac
(3)a2-a3
(4)4(m+n)2+2(m+n)
(5)9m 2n-6mn
(6)-6x2y-8xy2
公因式既可以是一个数、一个单项式的形式,也可以是一个多项式的形式.
典例精析
(1) 8a3b2 + 12ab3c;
例1 把下列各式分解因式
分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.
(2) 2a(b+c)-3(b+c).
典例精析
解:(1) 8a3b2 + 12ab3c
=4ab2 ·2a2+4ab2 ·3bc
=4ab2(2a2+3bc);
如果提出公因式4ab,另一个因式是否还有公式?
(2) 2a(b+c)-3(b+c)
=(b+c)(2a-3).
做整式乘法运算.
提公因式要尽量提,提彻底。
整体思想是数学中一种重要而且常用的思想方法.
如何检查因式分解是否正确?
小试牛刀
1.将下列各式因式分解:
(1)ax+ay;
(2)3mx-6my;
(3)8m2n+2mn;
(4)12xyz-9x2y2p;
(5)2a(y-z)-3b(z-y);
(6)p(a2+b2)-q(a2+b2).
(3)原式=2mn(m+1);
(1)原式=a(x+y);
(2)原式=3m(x-y);
(4)原式=3xy(4z-3xy);
(5)原式=(y-z)(2a+3b);
(6)原式=(a2+b2)(p-q).
小试牛刀
2.先分解因式,再求值.
小试牛刀
3.计算5×34+4×34+9×32.
解:原式=5×34+4×34+34
=(5+4+1)×34
=10×34
=810
课堂小结
今天我们收获了哪些知识?
1.什么是因式分解?因式分解与整式乘法之间有什么联系?
2.如何确定公因式?提公因式法的一般步骤是什么?
am+bm+mc=m(a+b+c)
三定,即定系数;定字母;定指数
互为逆运算
第一步找公因式;第二步提公因式
实战演练
1.下列从左到右的变形中是因式分解的有( )
①x2+2x+1=(x+1)2;
②x3+x=x(x2+1);
③(x-y)2=x2-2xy+y2;
④x2-25y2=(x+5y)(x-5y).
A.1个 B.2个 C.3个 D.4个
C
实战演练
2.下列多项式分解因式,正确的是( )
A.8abx-12a2x2=2ax(4b-6ax)
B.4x2-6xy+2x=2x(2x-3y)
C.-6x3+6x2-12x=-6x(x2-x+2)
D.-3a2y+9ay-6y=-3y(a2+3a-2)
C
实战演练
3.观察下列各组式子: ①2a+b和a+b; ②5m(a-b)和-a+b;
③3(a+b)和-a-b;④x2-y2和x2+y2. 其中有公因式的是
( )
A.①② B.②③ C.③④ D.①④
B
4.若多项式x2-mx-35分解因式为(x-5)(x+7),则m的值为( )
A.-2 B.2 C.12 D.-12
A
实战演练
6.分解因式:
(1)-7ab-14a2bx+49ab2y;(2)6x(a-b)+4y(b-a).
解:(1)原式=-7ab(1+2ax-7by)
(2)原式= 6x(a-b) - 4y(a-b)
= (a-b)(6x-4y)
= 2(a-b)(3x-2y)
5.若9a2(x-y)2-3a(y-x)3=M·(3a+x-y),则M等于___________.
3a(x-y)2
实战演练
解:(1)2x2y+xy2=xy(2x+y)=6×5=30.
(2)原式=(2x+1)[(2x+1)-(2x-1)]
=(2x+1)(2x+1-2x+1)=2(2x+1).
7.(1)已知: 2x+y=5,xy=6,求代数式2x2y+xy2的值.
(2)化简求值:(2x+1)2-(2x+1)(2x-1),其中x=3.
将x=3代入上式,
原式=14.
课后作业
教材119页练习题第1、4(1)题.
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
14.3.1因式分解---提公因式法
学习目标
1.理解因式分解的意义和概念及其与整式乘法的区别和联系.
(重点)
2.理解并掌握提公因式法并能熟练地运用提公因式法分解因式.(难点)
温故知新
2.填空:
1.说一说单项式乘以多项式的计算法则?
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
合作探究
请把下列多项式写成整式的乘积的形式:
像这样, 把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式.
因式分解与整式乘法有什么关系?
x2-1 (x+1)(x-1)
因式分解
整式乘法
是互为相反的变形,即:
小试牛刀
在下列等式中,从左到右的变形哪些是因式分解,不是的请说明理由.
①
②
③
④
⑤
⑥
am+bm+c=m(a+b)+c
24x2y=3x ·8xy
x2-1=(x+1)(x-1)
(2x+1)2=4x2+4x+1
x2+x=x2(1+ )
2x+4y+6z=2(x+2y+3z)
不是;最后不是积的运算
不是;因式分解的对象是多项式
不是;是整式乘法
不是;每个因式必须是整式
是
是
合作探究
pa+pb+pc
像上式,它的各项都有公共的因式P,我们把因式P叫做这个多项式各项的公因式.
公共的因式p
思考1: 观察下列多项式,它们有什么共同特点?
合作探究
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
( a+b+c )
可得pa+ pb +pc
p
=
由于 ( a+b+c )
=pa+ pb +pc
p
合作探究
找 3x 2 – 6 xy 的公因式.
系数:最大公约数
3
字母:相同的字母
x
公因式是3x
指数:相同字母的最低次数
1
思考2:如何确定一个多项式的公因式?
一看系数 二看字母 三看指数
最大公约数
相同字母
最低指数
小试牛刀
下列各多项式的公因式是什么?
2
a
a2
2(m+n)
3mn
-2xy
(1)2x+6y
(2)ab-2ac
(3)a2-a3
(4)4(m+n)2+2(m+n)
(5)9m 2n-6mn
(6)-6x2y-8xy2
公因式既可以是一个数、一个单项式的形式,也可以是一个多项式的形式.
典例精析
(1) 8a3b2 + 12ab3c;
例1 把下列各式分解因式
分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.
(2) 2a(b+c)-3(b+c).
典例精析
解:(1) 8a3b2 + 12ab3c
=4ab2 ·2a2+4ab2 ·3bc
=4ab2(2a2+3bc);
如果提出公因式4ab,另一个因式是否还有公式?
(2) 2a(b+c)-3(b+c)
=(b+c)(2a-3).
做整式乘法运算.
提公因式要尽量提,提彻底。
整体思想是数学中一种重要而且常用的思想方法.
如何检查因式分解是否正确?
小试牛刀
1.将下列各式因式分解:
(1)ax+ay;
(2)3mx-6my;
(3)8m2n+2mn;
(4)12xyz-9x2y2p;
(5)2a(y-z)-3b(z-y);
(6)p(a2+b2)-q(a2+b2).
(3)原式=2mn(m+1);
(1)原式=a(x+y);
(2)原式=3m(x-y);
(4)原式=3xy(4z-3xy);
(5)原式=(y-z)(2a+3b);
(6)原式=(a2+b2)(p-q).
小试牛刀
2.先分解因式,再求值.
小试牛刀
3.计算5×34+4×34+9×32.
解:原式=5×34+4×34+34
=(5+4+1)×34
=10×34
=810
课堂小结
今天我们收获了哪些知识?
1.什么是因式分解?因式分解与整式乘法之间有什么联系?
2.如何确定公因式?提公因式法的一般步骤是什么?
am+bm+mc=m(a+b+c)
三定,即定系数;定字母;定指数
互为逆运算
第一步找公因式;第二步提公因式
实战演练
1.下列从左到右的变形中是因式分解的有( )
①x2+2x+1=(x+1)2;
②x3+x=x(x2+1);
③(x-y)2=x2-2xy+y2;
④x2-25y2=(x+5y)(x-5y).
A.1个 B.2个 C.3个 D.4个
C
实战演练
2.下列多项式分解因式,正确的是( )
A.8abx-12a2x2=2ax(4b-6ax)
B.4x2-6xy+2x=2x(2x-3y)
C.-6x3+6x2-12x=-6x(x2-x+2)
D.-3a2y+9ay-6y=-3y(a2+3a-2)
C
实战演练
3.观察下列各组式子: ①2a+b和a+b; ②5m(a-b)和-a+b;
③3(a+b)和-a-b;④x2-y2和x2+y2. 其中有公因式的是
( )
A.①② B.②③ C.③④ D.①④
B
4.若多项式x2-mx-35分解因式为(x-5)(x+7),则m的值为( )
A.-2 B.2 C.12 D.-12
A
实战演练
6.分解因式:
(1)-7ab-14a2bx+49ab2y;(2)6x(a-b)+4y(b-a).
解:(1)原式=-7ab(1+2ax-7by)
(2)原式= 6x(a-b) - 4y(a-b)
= (a-b)(6x-4y)
= 2(a-b)(3x-2y)
5.若9a2(x-y)2-3a(y-x)3=M·(3a+x-y),则M等于___________.
3a(x-y)2
实战演练
解:(1)2x2y+xy2=xy(2x+y)=6×5=30.
(2)原式=(2x+1)[(2x+1)-(2x-1)]
=(2x+1)(2x+1-2x+1)=2(2x+1).
7.(1)已知: 2x+y=5,xy=6,求代数式2x2y+xy2的值.
(2)化简求值:(2x+1)2-(2x+1)(2x-1),其中x=3.
将x=3代入上式,
原式=14.
课后作业
教材119页练习题第1、4(1)题.
https://www.21cnjy.com/help/help_extract.php
