4.2.1平行线 课件(共20张PPT)
文档属性
| 名称 | 4.2.1平行线 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 14:17:59 | ||
图片预览







文档简介
(共20张PPT)
4.2.1 平行线
主讲:
华东师大版七年级上册
第4章 相交线与平行线
学习目标
目标
1
重难点
2
1.了解平行线的概念、平面内两条直线的相交和平行的两种位置关系, 知道平行公理以及平行公理的推论.
2.会用符号语方表示平行公理推论, 会用三角尺和直尺过已知直线外一点画这条直线的平行线.
重点:探索和掌握平行公理及其推论.
难点:对平行线本质属性的理解,用几何语言描述图形的性质.
新课导入
【提问】通过前面的课程学习,我们知道两条直线具有怎样位置关系?
两条直线相交(其中垂直是相交的特殊情形)
新课讲授
【提问】观察下面图形,你发现了什么?
两条直线没有交点
新课讲授
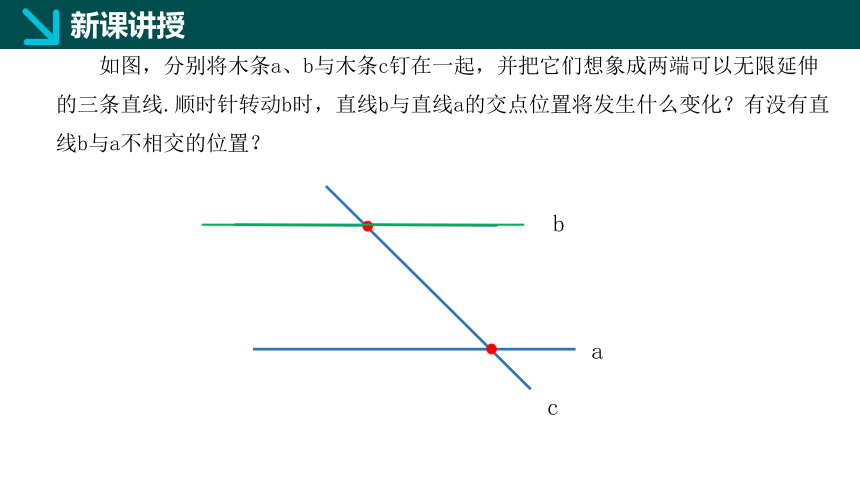
如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.顺时针转动b时,直线b与直线a的交点位置将发生什么变化?有没有直线b与a不相交的位置?
a
c
b
新课讲授
同一平面内, 不相交的两条直线叫做平行线.
a
b
【注意】
1.“在同一平面内”是前提条件.
2.“不相交”就是说两条直线没有交点.
3.平行线指的是“两条直线”而不是两条射线或两条线段.
新课讲授
平行线的表示方法:平行用符号“∥”表示,如直线a与直线b平行,
记作:a∥b,读作“a平行于b”.
a
b
注意:平行线是相互的,如直线a与直线b平行,
记作:a∥b,也可写成b∥a.
新课讲授
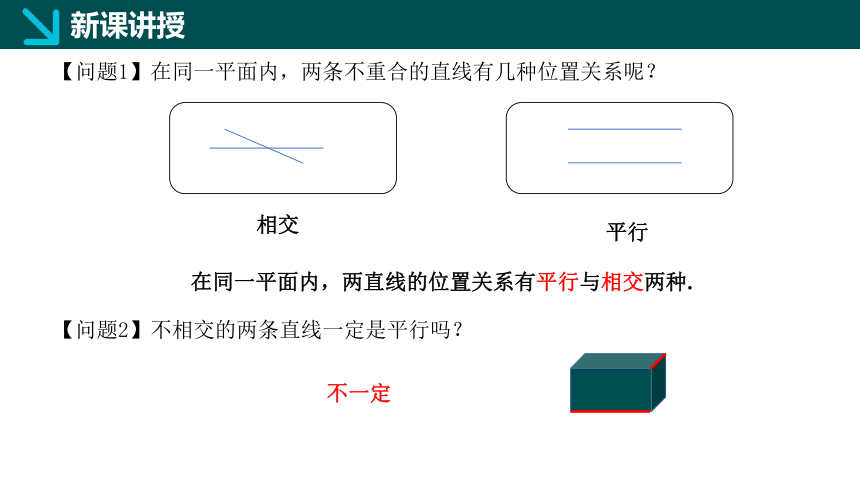
【问题1】在同一平面内,两条不重合的直线有几种位置关系呢?
【问题2】不相交的两条直线一定是平行吗?
相交
平行
不一定
在同一平面内,两直线的位置关系有平行与相交两种.
新课讲授
【问题3】你能举出一些其他平行的例子吗?
新课讲授
【问题4】已知直线a,你能画出直线a的平行线吗?
(1)放
(2)靠
(3)推
(4)画
平行线的画法 :一放、二靠、三推、四画.
新课讲授
【问题5】经过点B能画出几条直线?
【问题6】与直线a平行的直线有几条?
【问题7】经过点B能画出几条直线与直线a平行?
【问题8】你发现了什么?
a
B
b
无数条
1条
无数条
发现:经过直线外一点,有且只有一条直线与已知直线平行.
新课讲授
【问题9】过点C画一条直线与直线a平行,与问题7中所画的直线平行吗?
a
B
b
c
C
平行
新课讲授
平行线的性质(平行公理):经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
几何语言表达式:
∵ a∥b, b∥c (已知)
∴ a∥c (平行线的传递性)
c
b
a
课堂测试
1.下列说法:①同位角相等;②两条不相交的直线叫做平行线;③过一点有且只有一条直线与己知直线平行;④三条直线两两相交,总有三个交点;⑤三条直线a,b,c,若a∥b,b∥c,则a∥c.其中正确的个数是
A.1个 B.2个 C.3个 D.4个
2.下列生活实例:
①路口的斑马线;②天上的彩虹;③体操队的纵队;④百米跑道线;⑤平直的火车铁轨.其中属于平行线的有( )
A.1个 B.2个 C.3个 D.4个
A
D
课堂测试
3. 下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.对顶角一定相等
C.直线外一点到这条直线的垂线段,叫做点到直线的距离
D.互补的两个角是邻补角
4.已知∠AOB,P是任意一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
B
D
课堂测试
5.在同一平面内,a、b、c是直线,下列说法正确的是( )
A.若a∥b,b∥c 则 a∥c B.若a⊥b,b⊥c,则a⊥c
C.若a∥b,b⊥c,则a∥c D.若a∥b,b∥c,则a⊥c
6.同一平面内互不重合的三条直线的交点有 个
A
0或1或2或3
7.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为6cm,b与c的距离为1cm,则a与c的距离为( )
A.2cm B.3cm C.7cm或5cm D.1cm或3cm
C
课堂测试
8. 如图,将一张长方形的硬纸片对折,是折痕,把面平摊在桌面上,另一个面不论怎样改变位置,总有与平行,请你说出其中的道理.
【详解】解:∵长方形的硬纸片对折,是折痕,
∴,,
∴,
∴另一个面不论怎样改变位置,总有与平行.
课后小结
同一平面内, 不相交的两条直线叫做平行线.
平行线的性质(平行公理):经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
布置作业
主讲:
华东师大版七年级上册
感谢聆听
4.2.1 平行线
主讲:
华东师大版七年级上册
第4章 相交线与平行线
学习目标
目标
1
重难点
2
1.了解平行线的概念、平面内两条直线的相交和平行的两种位置关系, 知道平行公理以及平行公理的推论.
2.会用符号语方表示平行公理推论, 会用三角尺和直尺过已知直线外一点画这条直线的平行线.
重点:探索和掌握平行公理及其推论.
难点:对平行线本质属性的理解,用几何语言描述图形的性质.
新课导入
【提问】通过前面的课程学习,我们知道两条直线具有怎样位置关系?
两条直线相交(其中垂直是相交的特殊情形)
新课讲授
【提问】观察下面图形,你发现了什么?
两条直线没有交点
新课讲授
如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.顺时针转动b时,直线b与直线a的交点位置将发生什么变化?有没有直线b与a不相交的位置?
a
c
b
新课讲授
同一平面内, 不相交的两条直线叫做平行线.
a
b
【注意】
1.“在同一平面内”是前提条件.
2.“不相交”就是说两条直线没有交点.
3.平行线指的是“两条直线”而不是两条射线或两条线段.
新课讲授
平行线的表示方法:平行用符号“∥”表示,如直线a与直线b平行,
记作:a∥b,读作“a平行于b”.
a
b
注意:平行线是相互的,如直线a与直线b平行,
记作:a∥b,也可写成b∥a.
新课讲授
【问题1】在同一平面内,两条不重合的直线有几种位置关系呢?
【问题2】不相交的两条直线一定是平行吗?
相交
平行
不一定
在同一平面内,两直线的位置关系有平行与相交两种.
新课讲授
【问题3】你能举出一些其他平行的例子吗?
新课讲授
【问题4】已知直线a,你能画出直线a的平行线吗?
(1)放
(2)靠
(3)推
(4)画
平行线的画法 :一放、二靠、三推、四画.
新课讲授
【问题5】经过点B能画出几条直线?
【问题6】与直线a平行的直线有几条?
【问题7】经过点B能画出几条直线与直线a平行?
【问题8】你发现了什么?
a
B
b
无数条
1条
无数条
发现:经过直线外一点,有且只有一条直线与已知直线平行.
新课讲授
【问题9】过点C画一条直线与直线a平行,与问题7中所画的直线平行吗?
a
B
b
c
C
平行
新课讲授
平行线的性质(平行公理):经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
几何语言表达式:
∵ a∥b, b∥c (已知)
∴ a∥c (平行线的传递性)
c
b
a
课堂测试
1.下列说法:①同位角相等;②两条不相交的直线叫做平行线;③过一点有且只有一条直线与己知直线平行;④三条直线两两相交,总有三个交点;⑤三条直线a,b,c,若a∥b,b∥c,则a∥c.其中正确的个数是
A.1个 B.2个 C.3个 D.4个
2.下列生活实例:
①路口的斑马线;②天上的彩虹;③体操队的纵队;④百米跑道线;⑤平直的火车铁轨.其中属于平行线的有( )
A.1个 B.2个 C.3个 D.4个
A
D
课堂测试
3. 下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.对顶角一定相等
C.直线外一点到这条直线的垂线段,叫做点到直线的距离
D.互补的两个角是邻补角
4.已知∠AOB,P是任意一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
B
D
课堂测试
5.在同一平面内,a、b、c是直线,下列说法正确的是( )
A.若a∥b,b∥c 则 a∥c B.若a⊥b,b⊥c,则a⊥c
C.若a∥b,b⊥c,则a∥c D.若a∥b,b∥c,则a⊥c
6.同一平面内互不重合的三条直线的交点有 个
A
0或1或2或3
7.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为6cm,b与c的距离为1cm,则a与c的距离为( )
A.2cm B.3cm C.7cm或5cm D.1cm或3cm
C
课堂测试
8. 如图,将一张长方形的硬纸片对折,是折痕,把面平摊在桌面上,另一个面不论怎样改变位置,总有与平行,请你说出其中的道理.
【详解】解:∵长方形的硬纸片对折,是折痕,
∴,,
∴,
∴另一个面不论怎样改变位置,总有与平行.
课后小结
同一平面内, 不相交的两条直线叫做平行线.
平行线的性质(平行公理):经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
布置作业
主讲:
华东师大版七年级上册
感谢聆听
同课章节目录
