14.1平移(第1课时平移的概念与性质) 课件(共28张PPT)
文档属性
| 名称 | 14.1平移(第1课时平移的概念与性质) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
沪教版(2024)七年级数学上册 第十四章 图形的运动
14.1 平移
第一课时 平移的概念与性质
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
1.理解平移的概念及决定因素.(难点)
2.会找出平移前后图形中对应点、对应角和对应线段.
3.掌握平移的性质及其运用.(重点)
学习目标
生活中常见的衣橱移门,当推动门把手时,门会从一个位置沿轨道移动到另一个位置。
新知探究
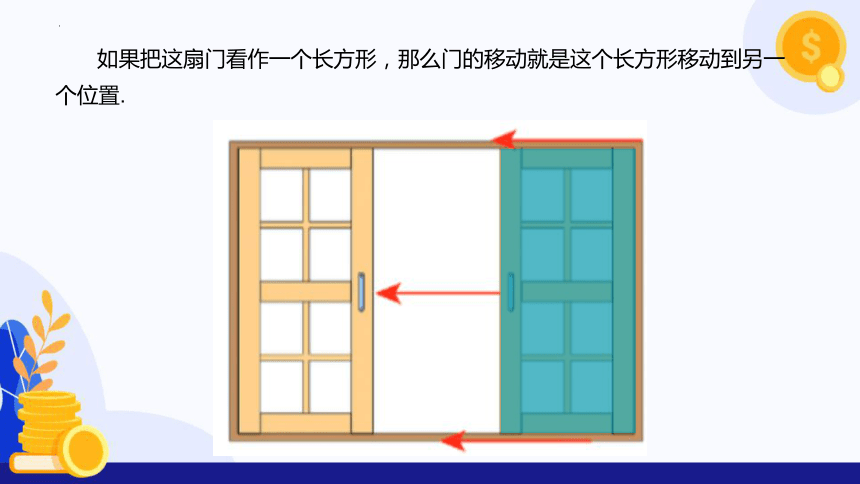
如果把这扇门看作一个长方形,那么门的移动就是这个长方形移动到另一个位置.
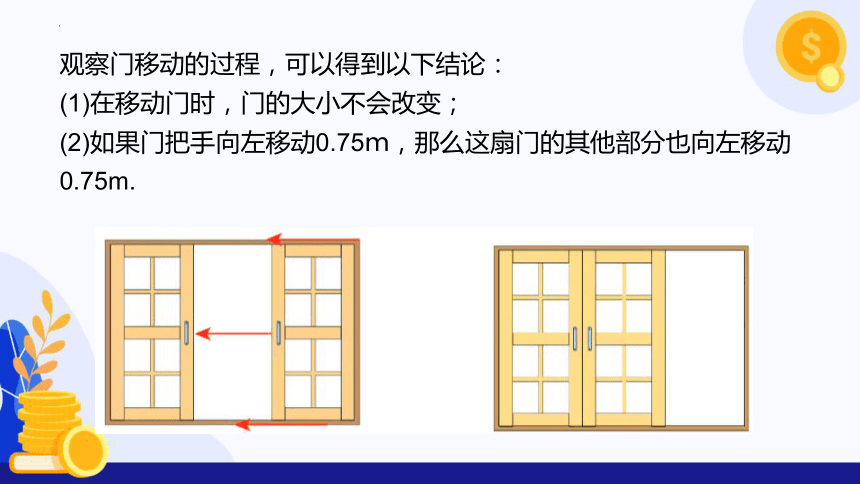
观察门移动的过程,可以得到以下结论:
(1)在移动门时,门的大小不会改变;
(2)如果门把手向左移动0.75m,那么这扇门的其他部分也向左移动
0.75m.
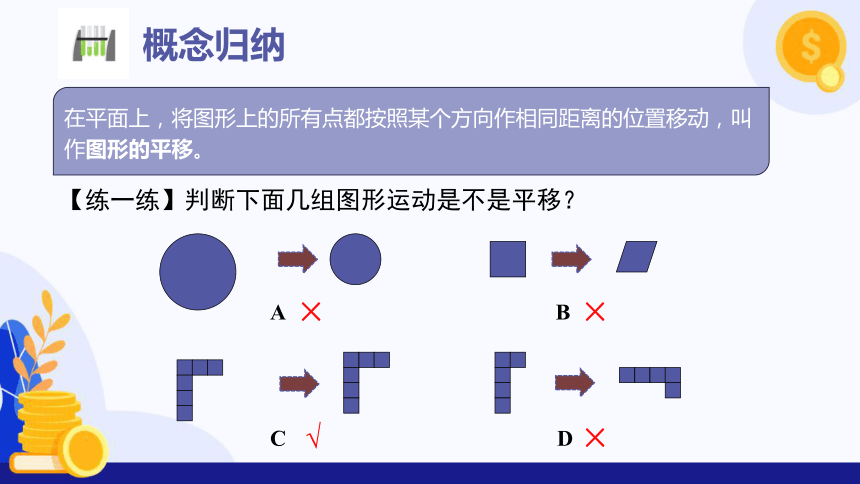
【练一练】判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
概念归纳
在平面上,将图形上的所有点都按照某个方向作相同距离的位置移动,叫作图形的平移。
如图,移动三角形ABC得到三角形A1B1C1.平移的方向为射线AA1的方向,平移的距离是线段AA1的长度.其中,点A与点A1是对应点;线段AB与线段A1B1是对应线段,它们的长度相等;∠BAC与∠B1A1C1是对应角,它们的大小也相等.
归纳总结
从上面的例子可以得到图形的平移具有以下性质:
(1)图形平移后,每组对应点之间的距离相等;
(2)对应点所连接的线段平行(或在同一直线上)且相等;
(3)对应角的大小相等;对应线段平行(或在同一直线上)且相等;
(4)平移后得到的图形与原图形形状相同,大小相等.
【练一练】经过平移,图形上每个点都沿同一个方向移动了一段距离.下面说法正确的是( )
A 不同的点移动的距离不同
B 不同的点移动的距离既可能相同也可能不同
C 不同的点移动的距离相同
D 无法确定
C
图形平移前后对应点之间的距离叫作图形平移的距离.
概念归纳
图形的平移在日常生活中有着广泛的应用,下图是由一个基本图形通过多次平移后得到的组合图形。
设计一个图案,使其由一个基本图形多次平移后组合得到
例1 如图14-1-4 ,将三角形ABC向右平移4格,再向下平移3格后的图形为三角形A1B1C1.
(1)点B、C的对应点分别是哪两个点?
(2)线段AC的对应线段是哪条线段?它们的长度相等吗?∠ABC的对应角是哪个角?它们的大小相等吗?
(3)如果线段AB的中点是D,那么能确定它的对应点的位置吗?
课本例题
解:
(2)线段AC的对应线段是哪条线段?它们的长度相等吗?∠ABC的对应角是哪个角?它们的大小相等吗?
(3)如果线段AB的中点是D,那么能确定它的对应点的位置吗?
(1)点B、C的对应点分别是哪两个点?
(1)点B、C的对应点分别是点B1、C1.
(2)线段AC的对应线段是A1C1,AC=A1C1;∠ABC的对应角是∠A1B1C1,
∠ABC=∠A1B1C1.
(3)线段AB的中点D的对应点的是线段A1B1的中点D1.
课本例题
在图 14-1-4 中画出三角形ABC 的平移方向,并量出平移的距离
1.如图,将(1)中的图形N平移到如(2)所示的位置,则下列图形N的平移方法中,正确的是( )
A.向下平移1格;
B.向上平移1格;
C.向上平移2格;
D.向下平移2格
D
课堂练习
2.如图,三角形A′B′C′由三角形ABC沿射线AC方向平移2cm得到.若AC=3cm,则A′C= .
1cm
课堂练习
3.如图,每个小方格的边长都是1个单位长度.平移后三角形甲与三角形乙重合.
右
(1)把三角形甲向 平移 个单位长度,再向 平移 个单位长度,便与三角形乙重合.
(2)要使这两个三角形重合,你还有其他平移的方法吗?请说出其中一种.
9
3
下
先向下平移3个单位,再向右平移9个单位。
课堂练习
1. [2023北京海淀区期中]卡塔尔世界杯吉祥物“拉伊卜”刷爆网络!如图是“拉伊卜”的形象图片,在下面的四个图形中,能由它经过平移得到的图形是
( D )
D
分层练习-基础
2.下列现象中,属于平移的是( D )
①小朋友在荡秋千; ②打气筒打气时,活塞的运动;
③钟摆的摆动; ④瓶装饮料在传送带上移动.
A.①② B.①③
C.②③ D.②④
D
3.线段AB是由线段CD经过平移得到的,则线段AB与线段CD的关系为( D )
A.相交 B.平行或相等
C.平行且相等 D.平行(或在同一直线上)且相等
D
4.如图,在10×6的网格中,每个小正方形的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下列平移步骤正确的是( A )
A.先向左平移5个单位长度,再向下平移2个单位长度
B.先向右平移5个单位长度,再向下平移2个单位长度
C.先向左平移5个单位长度,再向上平移2个单位长度
D.先向右平移5个单位长度,再向上平移2个单位长度
A
5. [2023通辽]如图,用平移的方法说明平行四边形的面积公式S=ah时,若三角形ABE平移到三角形DCF,a=4,h=3,则三角形ABE的平移距离为( B )
A.3 B.4 C.5 D.12
B
6.如图,将三角形ABC平移后得到三角形DEF,若∠A=44°,∠EGC=70°,则∠ACB的度数是 26° .
26°
7. 【学科素养 模型观念】如图,小温同学在美术课上将三角形ABC通过平移设计得到“一棵树”,已知底边AB上的高CD为5 cm,沿CD方向向下平移3 cm到三角形A1B1C1的位置,再经过相同的平移到三角形A2B2C2的位置,下方树干EF长为6 cm,则树的高度CF长为( B )cm.
A.19 B.17 C.15 D.11
B
分层练习-巩固
8.如图,将三角形ABC沿着某一方向平移一定的距离得到三角形DEF,则下列结论:
①AD∥CF;②AC=DF;③∠ABC=∠DFE;
④∠DAE=∠AEB.
正确的有 ①②④ (填序号).
①②④
9.如图,∠1=70°,将直线m向右平移到直线n处,则∠2-∠3= 110° .
110°
点拨:如图,作直线l∥n,把∠2分为∠4和∠5,∴∠3=∠4.
由平移的性质得m∥n,
∴l∥m,∴∠1+∠5=180°.
∵∠1=70°,
∴∠2-∠3=∠4+∠5-∠3=∠5=180°-∠1=180°-70°=110°.
10. 【学科素养 应用意识】某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则三种造型所用铁丝的长度中最长的是 丙 .
丙
11.小明家新建了一栋楼房,装修时准备在楼梯上铺设地毯,已知这种地毯每平方米售价为50元,楼梯宽2 m,其侧面如图所示,则买地毯至少需要 550 元.
550
点拨:利用平移线段,把楼梯的横竖向上向右平移,构成一个长方形,长、宽分别为3 m,2.5 m,则地毯的长度为3+2.5=5.5(m),面积为5.5×2=11(m2),
故买地毯至少需要11×50=550(元).
12.如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF.已知BE=5,EF=8,CG=3,求图中阴影部分的面积.
解:∵直角三角形ABC沿AB方向平移得到直角三角形DEF,
∴三角形ABC的面积与三角形DEF的面积相等,
BC=EF,BC∥EF.
∴三角形ABC的面积-三角形DBG的面积=三角形DEF的面积-三角形DBG的面积,四边形GBEF为梯形.∴阴影部分的面积与梯形GBEF的面积相等.
∵EF=8,CG=3,∴BG=BC-CG=EF-CG=5.
又∵BE=5,∴阴影部分的面积为(5+8)×5×=32.5.
分层练习-拓展
课堂小结
1.平移的概念
在平面上,将图形上的所有点都按照某个方向作相同距离的位置移动,叫作图形的平移。
2.平移的性质:
(1)图形平移后,每组对应点之间的距离相等;
(2)对应点所连接的线段平行(或在同一直线上)且相等;
(3)对应角的大小相等;对应线段平行(或在同一直线上)且相等;
(4)平移后得到的图形与原图形形状相同,大小相等.
3.平移的距离
图形平移前后对应点之间的距离叫作图形平移的距离.
沪教版(2024)七年级数学上册 第十四章 图形的运动
14.1 平移
第一课时 平移的概念与性质
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
1.理解平移的概念及决定因素.(难点)
2.会找出平移前后图形中对应点、对应角和对应线段.
3.掌握平移的性质及其运用.(重点)
学习目标
生活中常见的衣橱移门,当推动门把手时,门会从一个位置沿轨道移动到另一个位置。
新知探究
如果把这扇门看作一个长方形,那么门的移动就是这个长方形移动到另一个位置.
观察门移动的过程,可以得到以下结论:
(1)在移动门时,门的大小不会改变;
(2)如果门把手向左移动0.75m,那么这扇门的其他部分也向左移动
0.75m.
【练一练】判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
概念归纳
在平面上,将图形上的所有点都按照某个方向作相同距离的位置移动,叫作图形的平移。
如图,移动三角形ABC得到三角形A1B1C1.平移的方向为射线AA1的方向,平移的距离是线段AA1的长度.其中,点A与点A1是对应点;线段AB与线段A1B1是对应线段,它们的长度相等;∠BAC与∠B1A1C1是对应角,它们的大小也相等.
归纳总结
从上面的例子可以得到图形的平移具有以下性质:
(1)图形平移后,每组对应点之间的距离相等;
(2)对应点所连接的线段平行(或在同一直线上)且相等;
(3)对应角的大小相等;对应线段平行(或在同一直线上)且相等;
(4)平移后得到的图形与原图形形状相同,大小相等.
【练一练】经过平移,图形上每个点都沿同一个方向移动了一段距离.下面说法正确的是( )
A 不同的点移动的距离不同
B 不同的点移动的距离既可能相同也可能不同
C 不同的点移动的距离相同
D 无法确定
C
图形平移前后对应点之间的距离叫作图形平移的距离.
概念归纳
图形的平移在日常生活中有着广泛的应用,下图是由一个基本图形通过多次平移后得到的组合图形。
设计一个图案,使其由一个基本图形多次平移后组合得到
例1 如图14-1-4 ,将三角形ABC向右平移4格,再向下平移3格后的图形为三角形A1B1C1.
(1)点B、C的对应点分别是哪两个点?
(2)线段AC的对应线段是哪条线段?它们的长度相等吗?∠ABC的对应角是哪个角?它们的大小相等吗?
(3)如果线段AB的中点是D,那么能确定它的对应点的位置吗?
课本例题
解:
(2)线段AC的对应线段是哪条线段?它们的长度相等吗?∠ABC的对应角是哪个角?它们的大小相等吗?
(3)如果线段AB的中点是D,那么能确定它的对应点的位置吗?
(1)点B、C的对应点分别是哪两个点?
(1)点B、C的对应点分别是点B1、C1.
(2)线段AC的对应线段是A1C1,AC=A1C1;∠ABC的对应角是∠A1B1C1,
∠ABC=∠A1B1C1.
(3)线段AB的中点D的对应点的是线段A1B1的中点D1.
课本例题
在图 14-1-4 中画出三角形ABC 的平移方向,并量出平移的距离
1.如图,将(1)中的图形N平移到如(2)所示的位置,则下列图形N的平移方法中,正确的是( )
A.向下平移1格;
B.向上平移1格;
C.向上平移2格;
D.向下平移2格
D
课堂练习
2.如图,三角形A′B′C′由三角形ABC沿射线AC方向平移2cm得到.若AC=3cm,则A′C= .
1cm
课堂练习
3.如图,每个小方格的边长都是1个单位长度.平移后三角形甲与三角形乙重合.
右
(1)把三角形甲向 平移 个单位长度,再向 平移 个单位长度,便与三角形乙重合.
(2)要使这两个三角形重合,你还有其他平移的方法吗?请说出其中一种.
9
3
下
先向下平移3个单位,再向右平移9个单位。
课堂练习
1. [2023北京海淀区期中]卡塔尔世界杯吉祥物“拉伊卜”刷爆网络!如图是“拉伊卜”的形象图片,在下面的四个图形中,能由它经过平移得到的图形是
( D )
D
分层练习-基础
2.下列现象中,属于平移的是( D )
①小朋友在荡秋千; ②打气筒打气时,活塞的运动;
③钟摆的摆动; ④瓶装饮料在传送带上移动.
A.①② B.①③
C.②③ D.②④
D
3.线段AB是由线段CD经过平移得到的,则线段AB与线段CD的关系为( D )
A.相交 B.平行或相等
C.平行且相等 D.平行(或在同一直线上)且相等
D
4.如图,在10×6的网格中,每个小正方形的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下列平移步骤正确的是( A )
A.先向左平移5个单位长度,再向下平移2个单位长度
B.先向右平移5个单位长度,再向下平移2个单位长度
C.先向左平移5个单位长度,再向上平移2个单位长度
D.先向右平移5个单位长度,再向上平移2个单位长度
A
5. [2023通辽]如图,用平移的方法说明平行四边形的面积公式S=ah时,若三角形ABE平移到三角形DCF,a=4,h=3,则三角形ABE的平移距离为( B )
A.3 B.4 C.5 D.12
B
6.如图,将三角形ABC平移后得到三角形DEF,若∠A=44°,∠EGC=70°,则∠ACB的度数是 26° .
26°
7. 【学科素养 模型观念】如图,小温同学在美术课上将三角形ABC通过平移设计得到“一棵树”,已知底边AB上的高CD为5 cm,沿CD方向向下平移3 cm到三角形A1B1C1的位置,再经过相同的平移到三角形A2B2C2的位置,下方树干EF长为6 cm,则树的高度CF长为( B )cm.
A.19 B.17 C.15 D.11
B
分层练习-巩固
8.如图,将三角形ABC沿着某一方向平移一定的距离得到三角形DEF,则下列结论:
①AD∥CF;②AC=DF;③∠ABC=∠DFE;
④∠DAE=∠AEB.
正确的有 ①②④ (填序号).
①②④
9.如图,∠1=70°,将直线m向右平移到直线n处,则∠2-∠3= 110° .
110°
点拨:如图,作直线l∥n,把∠2分为∠4和∠5,∴∠3=∠4.
由平移的性质得m∥n,
∴l∥m,∴∠1+∠5=180°.
∵∠1=70°,
∴∠2-∠3=∠4+∠5-∠3=∠5=180°-∠1=180°-70°=110°.
10. 【学科素养 应用意识】某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则三种造型所用铁丝的长度中最长的是 丙 .
丙
11.小明家新建了一栋楼房,装修时准备在楼梯上铺设地毯,已知这种地毯每平方米售价为50元,楼梯宽2 m,其侧面如图所示,则买地毯至少需要 550 元.
550
点拨:利用平移线段,把楼梯的横竖向上向右平移,构成一个长方形,长、宽分别为3 m,2.5 m,则地毯的长度为3+2.5=5.5(m),面积为5.5×2=11(m2),
故买地毯至少需要11×50=550(元).
12.如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF.已知BE=5,EF=8,CG=3,求图中阴影部分的面积.
解:∵直角三角形ABC沿AB方向平移得到直角三角形DEF,
∴三角形ABC的面积与三角形DEF的面积相等,
BC=EF,BC∥EF.
∴三角形ABC的面积-三角形DBG的面积=三角形DEF的面积-三角形DBG的面积,四边形GBEF为梯形.∴阴影部分的面积与梯形GBEF的面积相等.
∵EF=8,CG=3,∴BG=BC-CG=EF-CG=5.
又∵BE=5,∴阴影部分的面积为(5+8)×5×=32.5.
分层练习-拓展
课堂小结
1.平移的概念
在平面上,将图形上的所有点都按照某个方向作相同距离的位置移动,叫作图形的平移。
2.平移的性质:
(1)图形平移后,每组对应点之间的距离相等;
(2)对应点所连接的线段平行(或在同一直线上)且相等;
(3)对应角的大小相等;对应线段平行(或在同一直线上)且相等;
(4)平移后得到的图形与原图形形状相同,大小相等.
3.平移的距离
图形平移前后对应点之间的距离叫作图形平移的距离.
同课章节目录
