1.4.1 用空间向量研究直线、平面的位置关系-空间中直线与平面的垂直 课后训练(含解析)-2024-2025学年数学人教A版(2019)选择性必修第一册.
文档属性
| 名称 | 1.4.1 用空间向量研究直线、平面的位置关系-空间中直线与平面的垂直 课后训练(含解析)-2024-2025学年数学人教A版(2019)选择性必修第一册. |
|
|
| 格式 | docx | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 00:00:00 | ||
图片预览



文档简介
1.4.1 用空间向量研究直线、平面的位置关系
空间中直线与平面的垂直
A级——基础过关练
1.已知直线l与平面α垂直,直线l的一个方向向量为u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z等于( )
A.3 B.6
C.-9 D.9
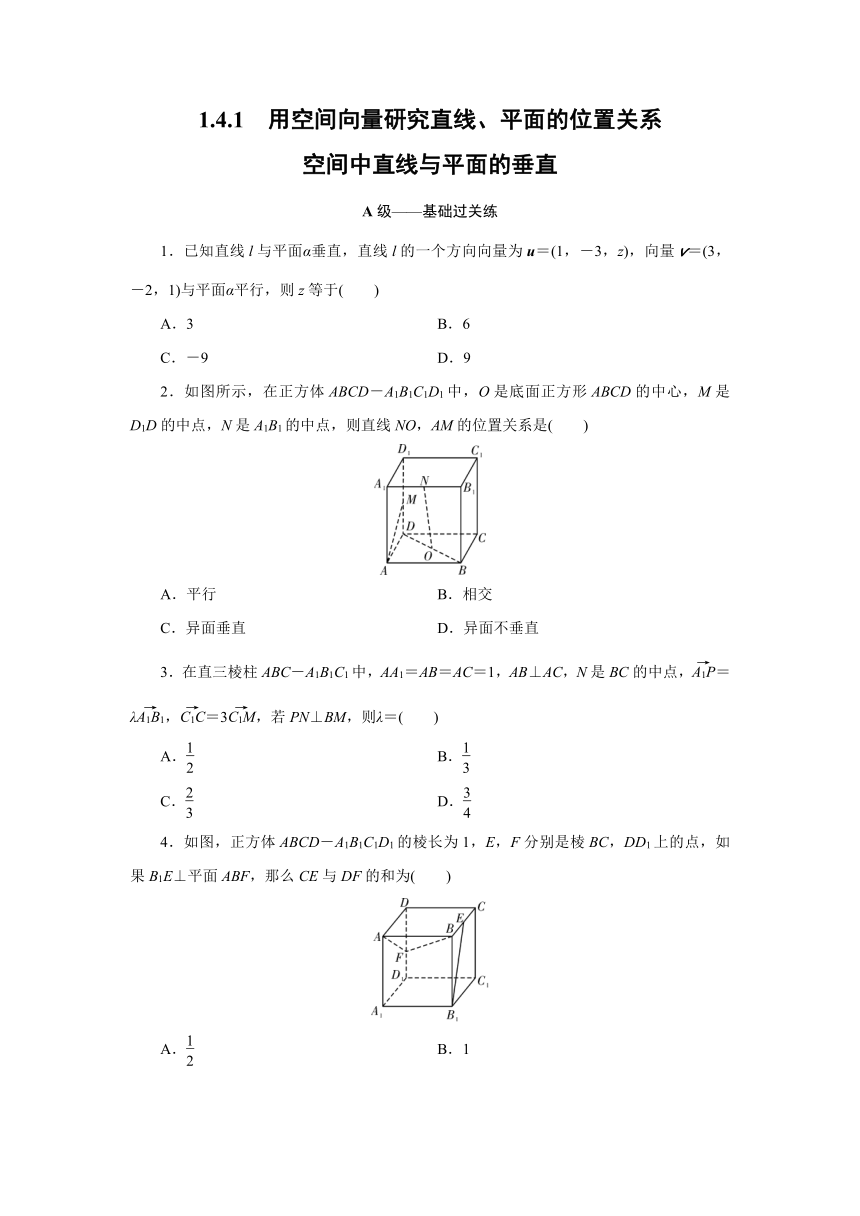
2.如图所示,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则直线NO,AM的位置关系是( )
A.平行 B.相交
C.异面垂直 D.异面不垂直
3.在直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,N是BC的中点,=λ,=3,若PN⊥BM,则λ=( )
A. B.
C. D.
4.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱BC,DD1上的点,如果B1E⊥平面ABF,那么CE与DF的和为( )
A. B.1
C. D.2
5.(多选)如图,以等腰直角三角形ABC斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出如下四个结论,其中正确的有( )
A.·=0
B.AB⊥DC
C.BD⊥AC
D.平面ADC的法向量和平面ABC的法向量互相垂直
6.(多选)已知P是平行四边形ABCD所在的平面外一点.若=(2,-1,-4),=(4,2,0),=(-1,2,-1),则下列结论正确的有( )
A.AP⊥AB B.AP⊥AD
C.是平面ABCD的法向量 D.∥
7.已知平面α的一个法向量a=(x,1,-2),平面β的一个法向量b=,若α⊥β,则x-y=________.
8.已知△ABC是以∠B为直角的等腰直角三角形,其中=(1,m,2),=(2,m,n)(m,n∈R),则m+n=________.
9.给出下列命题:
①直线l的方向向量为a=(1,-1,2),直线m的方向向量为b=,则l与m垂直;
②直线l的方向向量为a=(0,1,-1),平面α的法向量为n=(1,-1,-1),则l⊥α;
③平面α,β的法向量分别为n1=(0,1,3),n2=(1,0,2),则α∥β;
④平面α经过三点A(1,0,-1),B(0,1,0),C(-1,2,0),向量n=(1,u,t)是平面α的法向量,则u+t=1.
其中真命题是________(写出所有真命题的序号).
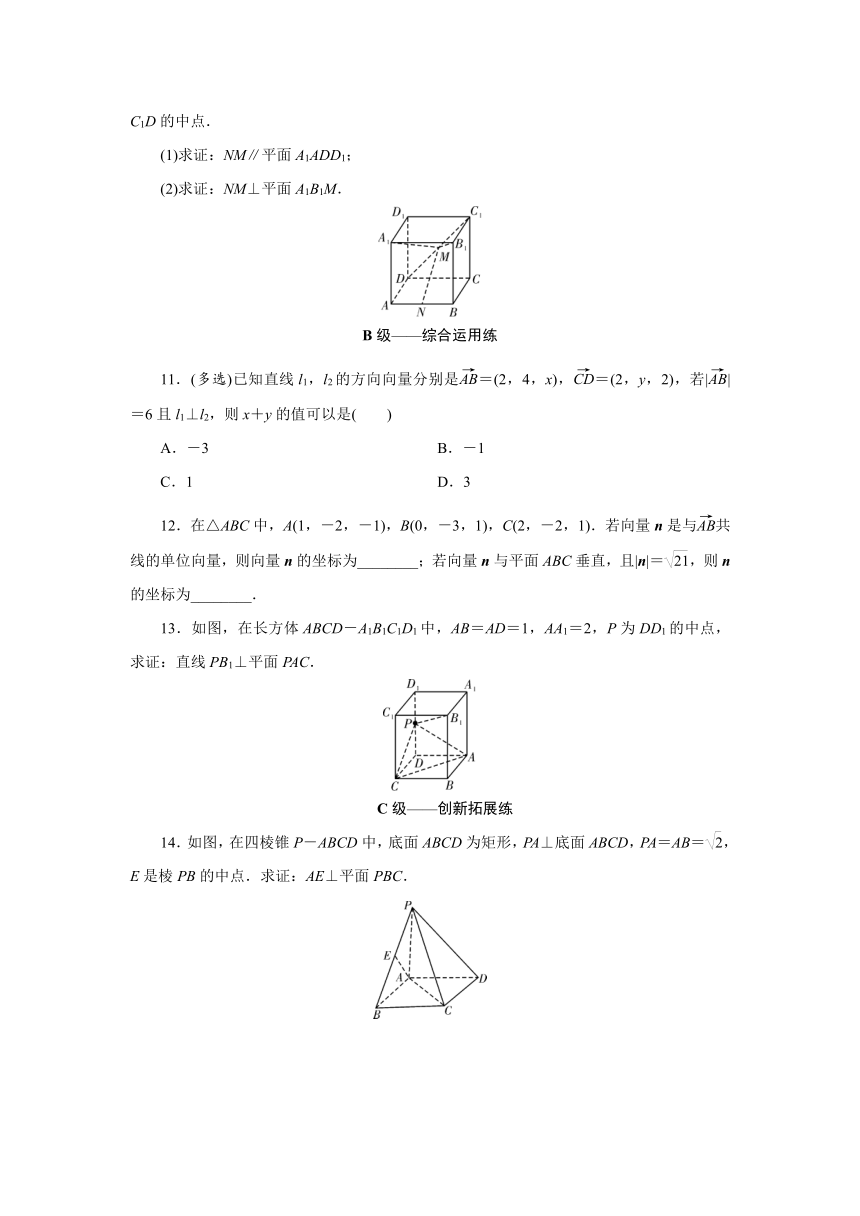
10.如图,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N,M分别是AB,C1D的中点.
(1)求证:NM∥平面A1ADD1;
(2)求证:NM⊥平面A1B1M.
B级——综合运用练
11.(多选)已知直线l1,l2的方向向量分别是=(2,4,x),=(2,y,2),若||=6且l1⊥l2,则x+y的值可以是( )
A.-3 B.-1
C.1 D.3
12.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量n是与共线的单位向量,则向量n的坐标为________;若向量n与平面ABC垂直,且|n|=,则n的坐标为________.
13.如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,P为DD1的中点,求证:直线PB1⊥平面PAC.
C级——创新拓展练
14.如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=,E是棱PB的中点.求证:AE⊥平面PBC.
答案解析
1、【答案】C
【解析】∵l⊥α,v与平面α平行,∴u⊥v,即u·v=0,∴1×3+3×2+z×1=0,∴z=-9.
2、【答案】C
【解析】建立空间直角坐标系,如图所示.设正方体的棱长为2,则A(2,0,0),M(0,0,1),O(1,1,0),N(2,1,2),∴=(-1,0,-2),=(-2,0,1).∵·=0,∴直线NO,AM的位置关系是异面垂直.
3、【答案】C
【解析】建立如图所示的空间直角坐标系.由题意知A1(0,0,0),B(1,0,1),M,P(λ,0,0),N,则=,=.∵⊥,∴×(-1)+×1+1×=0,∴λ=.故选C.
4、【答案】B
【解析】以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴、y轴、z轴建立空间直角坐标系(图略),设CE=x,DF=y,则易知E(x,1,1),B1(1,1,0),F(0,0,1-y),B(1,1,1),所以=(x-1,0,1),=(1,1,y).因为B1E⊥平面ABF,所以·=(1,1,y)·(x-1,0,1)=0,即x+y=1.
5、【答案】BC
【解析】建立以D为坐标原点,DB,DC,DA所在直线分别为x轴、y轴、z轴的空间直角坐标系(图略),设等腰直角三角形ABC的斜边BC=2,则B(1,0,0),C(0,1,0),D(0,0,0),A(0,0,1),=(1,0,-1),=(0,1,-1),=(0,1,0),=(-1,0,0),从而有·=0+0+1=1,故A错误;·=0,故B正确;·=0,故C正确;易知平面ADC的一个法向量为向量=(-1,0,0),设平面ABC的法向量为n=(x,y,z),则·n=x-z=0,·n=y-z=0,令y=1,则x=1,z=1,故n=(1,1,1),·n=-1,故D错误.
6、【答案】ABC
【解析】∵·=0,·=0,∴AB⊥AP,AD⊥AP,∴A,B正确;又∵与不平行,∴是平面ABCD的法向量,∴C正确;∵=-=(2,3,4),=(-1,2,-1),∴与不平行,∴D错误.
7、【答案】-1
【解析】因为α⊥β,所以a⊥b,所以-x+y-1=0,得x-y=-1.
8、【答案】-1
【解析】由题意得·=0,且||=||,∴∴∴m+n=-1.
9、【答案】①④
【解析】对于①,∵a=(1,-1,2),b=,∴a·b=1×2-1×1+2×=0,∴a⊥b,∴直线l与m垂直,故①正确;对于②,a=(0,1,-1),n=(1,-1,-1),∴a·n=0×1+1×(-1)+(-1)×(-1)=0,∴a⊥n,∴l∥α或l α,故②错误;对于③,∵n1=(0,1,3),n2=(1,0,2),∴n1与n2不共线,∴α∥β不成立,故③错误;对于④,∵点A(1,0,-1),B(0,1,0),C(-1,2,0),∴=(-1,1,1),=(-1,1,0),∵向量n=(1,u,t)是平面α的法向量,∴即则u+t=1,故④正确.综上,真命题是①④.
10、证明:(1)以点D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则A(1,0,0),M(0,1,1),N(1,1,0),B1(1,2,2),A1(1,0,2),
=(-1,0,1),
易知平面A1ADD1的一个法向量为m=(0,1,0),
因为·m=-1×0+0×1+1×0=0,
所以⊥m.
因为NM 平面A1ADD1,
所以NM∥平面A1ADD1.
(2)设平面A1B1M的法向量为n=(x,y,z),
=(0,2,0),=(-1,1,-1),
由
得取x=-1,可得n=(-1,0,1),
所以=n,故NM⊥平面A1B1M.
11、【答案】AC
【解析】=(2,4,x),=(2,y,2),若||=6且l1⊥l2,
则解得或所以x+y=1或-3.故选AC.
12、【答案】或 (-2,4,1)或(2,-4,-1)
【解析】据题意得=(-1,-1,2),=(1,0,2).设n=(x,y,z),若向量n是与共线的单位向量,则可得n=或n=.若n与平面ABC垂直,则即可得又因为|n|=,所以=,解得z=1或z=-1.所以n=(-2,4,1)或n=(2,-4,-1).
13、证明:依题设,以D为坐标原点,建立如图所示的空间直角坐标系Dxyz,则C(1,0,0),P(0,0,1),A(0,1,0),B1(1,1,2),
于是=(-1,1,0),=(-1,0,1),=(1,1,1),
所以·=(-1,1,0)·(1,1,1)=0,
·=(-1,0,1)·(1,1,1)=0,
故⊥,⊥,即PB1⊥CP,PB1⊥CA.
又因为CP∩CA=C,且CP 平面PAC,CA 平面PAC,
所以直线PB1⊥平面PAC.
14、证明:如图所示,以A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系Axyz.
设D(0,a,0),则A(0,0,0),B(,0,0),C(,a,0),P(0,0,),E.
于是=,=(0,a,0),=(,a,-),
则·=0,·=0.
所以AE⊥BC,AE⊥PC.
又因为BC∩PC=C,所以AE⊥平面PBC.
空间中直线与平面的垂直
A级——基础过关练
1.已知直线l与平面α垂直,直线l的一个方向向量为u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z等于( )
A.3 B.6
C.-9 D.9
2.如图所示,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则直线NO,AM的位置关系是( )
A.平行 B.相交
C.异面垂直 D.异面不垂直
3.在直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,N是BC的中点,=λ,=3,若PN⊥BM,则λ=( )
A. B.
C. D.
4.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱BC,DD1上的点,如果B1E⊥平面ABF,那么CE与DF的和为( )
A. B.1
C. D.2
5.(多选)如图,以等腰直角三角形ABC斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出如下四个结论,其中正确的有( )
A.·=0
B.AB⊥DC
C.BD⊥AC
D.平面ADC的法向量和平面ABC的法向量互相垂直
6.(多选)已知P是平行四边形ABCD所在的平面外一点.若=(2,-1,-4),=(4,2,0),=(-1,2,-1),则下列结论正确的有( )
A.AP⊥AB B.AP⊥AD
C.是平面ABCD的法向量 D.∥
7.已知平面α的一个法向量a=(x,1,-2),平面β的一个法向量b=,若α⊥β,则x-y=________.
8.已知△ABC是以∠B为直角的等腰直角三角形,其中=(1,m,2),=(2,m,n)(m,n∈R),则m+n=________.
9.给出下列命题:
①直线l的方向向量为a=(1,-1,2),直线m的方向向量为b=,则l与m垂直;
②直线l的方向向量为a=(0,1,-1),平面α的法向量为n=(1,-1,-1),则l⊥α;
③平面α,β的法向量分别为n1=(0,1,3),n2=(1,0,2),则α∥β;
④平面α经过三点A(1,0,-1),B(0,1,0),C(-1,2,0),向量n=(1,u,t)是平面α的法向量,则u+t=1.
其中真命题是________(写出所有真命题的序号).
10.如图,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N,M分别是AB,C1D的中点.
(1)求证:NM∥平面A1ADD1;
(2)求证:NM⊥平面A1B1M.
B级——综合运用练
11.(多选)已知直线l1,l2的方向向量分别是=(2,4,x),=(2,y,2),若||=6且l1⊥l2,则x+y的值可以是( )
A.-3 B.-1
C.1 D.3
12.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量n是与共线的单位向量,则向量n的坐标为________;若向量n与平面ABC垂直,且|n|=,则n的坐标为________.
13.如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,P为DD1的中点,求证:直线PB1⊥平面PAC.
C级——创新拓展练
14.如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=,E是棱PB的中点.求证:AE⊥平面PBC.
答案解析
1、【答案】C
【解析】∵l⊥α,v与平面α平行,∴u⊥v,即u·v=0,∴1×3+3×2+z×1=0,∴z=-9.
2、【答案】C
【解析】建立空间直角坐标系,如图所示.设正方体的棱长为2,则A(2,0,0),M(0,0,1),O(1,1,0),N(2,1,2),∴=(-1,0,-2),=(-2,0,1).∵·=0,∴直线NO,AM的位置关系是异面垂直.
3、【答案】C
【解析】建立如图所示的空间直角坐标系.由题意知A1(0,0,0),B(1,0,1),M,P(λ,0,0),N,则=,=.∵⊥,∴×(-1)+×1+1×=0,∴λ=.故选C.
4、【答案】B
【解析】以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴、y轴、z轴建立空间直角坐标系(图略),设CE=x,DF=y,则易知E(x,1,1),B1(1,1,0),F(0,0,1-y),B(1,1,1),所以=(x-1,0,1),=(1,1,y).因为B1E⊥平面ABF,所以·=(1,1,y)·(x-1,0,1)=0,即x+y=1.
5、【答案】BC
【解析】建立以D为坐标原点,DB,DC,DA所在直线分别为x轴、y轴、z轴的空间直角坐标系(图略),设等腰直角三角形ABC的斜边BC=2,则B(1,0,0),C(0,1,0),D(0,0,0),A(0,0,1),=(1,0,-1),=(0,1,-1),=(0,1,0),=(-1,0,0),从而有·=0+0+1=1,故A错误;·=0,故B正确;·=0,故C正确;易知平面ADC的一个法向量为向量=(-1,0,0),设平面ABC的法向量为n=(x,y,z),则·n=x-z=0,·n=y-z=0,令y=1,则x=1,z=1,故n=(1,1,1),·n=-1,故D错误.
6、【答案】ABC
【解析】∵·=0,·=0,∴AB⊥AP,AD⊥AP,∴A,B正确;又∵与不平行,∴是平面ABCD的法向量,∴C正确;∵=-=(2,3,4),=(-1,2,-1),∴与不平行,∴D错误.
7、【答案】-1
【解析】因为α⊥β,所以a⊥b,所以-x+y-1=0,得x-y=-1.
8、【答案】-1
【解析】由题意得·=0,且||=||,∴∴∴m+n=-1.
9、【答案】①④
【解析】对于①,∵a=(1,-1,2),b=,∴a·b=1×2-1×1+2×=0,∴a⊥b,∴直线l与m垂直,故①正确;对于②,a=(0,1,-1),n=(1,-1,-1),∴a·n=0×1+1×(-1)+(-1)×(-1)=0,∴a⊥n,∴l∥α或l α,故②错误;对于③,∵n1=(0,1,3),n2=(1,0,2),∴n1与n2不共线,∴α∥β不成立,故③错误;对于④,∵点A(1,0,-1),B(0,1,0),C(-1,2,0),∴=(-1,1,1),=(-1,1,0),∵向量n=(1,u,t)是平面α的法向量,∴即则u+t=1,故④正确.综上,真命题是①④.
10、证明:(1)以点D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则A(1,0,0),M(0,1,1),N(1,1,0),B1(1,2,2),A1(1,0,2),
=(-1,0,1),
易知平面A1ADD1的一个法向量为m=(0,1,0),
因为·m=-1×0+0×1+1×0=0,
所以⊥m.
因为NM 平面A1ADD1,
所以NM∥平面A1ADD1.
(2)设平面A1B1M的法向量为n=(x,y,z),
=(0,2,0),=(-1,1,-1),
由
得取x=-1,可得n=(-1,0,1),
所以=n,故NM⊥平面A1B1M.
11、【答案】AC
【解析】=(2,4,x),=(2,y,2),若||=6且l1⊥l2,
则解得或所以x+y=1或-3.故选AC.
12、【答案】或 (-2,4,1)或(2,-4,-1)
【解析】据题意得=(-1,-1,2),=(1,0,2).设n=(x,y,z),若向量n是与共线的单位向量,则可得n=或n=.若n与平面ABC垂直,则即可得又因为|n|=,所以=,解得z=1或z=-1.所以n=(-2,4,1)或n=(2,-4,-1).
13、证明:依题设,以D为坐标原点,建立如图所示的空间直角坐标系Dxyz,则C(1,0,0),P(0,0,1),A(0,1,0),B1(1,1,2),
于是=(-1,1,0),=(-1,0,1),=(1,1,1),
所以·=(-1,1,0)·(1,1,1)=0,
·=(-1,0,1)·(1,1,1)=0,
故⊥,⊥,即PB1⊥CP,PB1⊥CA.
又因为CP∩CA=C,且CP 平面PAC,CA 平面PAC,
所以直线PB1⊥平面PAC.
14、证明:如图所示,以A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系Axyz.
设D(0,a,0),则A(0,0,0),B(,0,0),C(,a,0),P(0,0,),E.
于是=,=(0,a,0),=(,a,-),
则·=0,·=0.
所以AE⊥BC,AE⊥PC.
又因为BC∩PC=C,所以AE⊥平面PBC.
