第二章 直线和圆的方程 章末检测(含解析)-2024-2025学年数学人教A版(2019)选择性必修第一册.
文档属性
| 名称 | 第二章 直线和圆的方程 章末检测(含解析)-2024-2025学年数学人教A版(2019)选择性必修第一册. |

|
|
| 格式 | docx | ||
| 文件大小 | 64.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 00:00:00 | ||
图片预览



文档简介
第二章 直线和圆的方程
章末检测
(时间:120分钟,满分150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线2x-2y+1=0的倾斜角是( )
A. B.
C. D.
2.圆C1:x2+y2+2x+8y-8=0与圆C2:x2+y2-4x-4y-1=0的位置关系是( )
A.外离 B.外切
C.相交 D.内含
3.圆C:x2+y2+6x-8y+24=0关于直线y=x对称的圆的方程为( )
A.(x-4)2+(y+3)2=1 B.(x-4)2+(y-3)2=49
C.(x+4)2+(y-3)2=1 D.(x+4)2+(y+3)2=49
4.已知直线l1:ax+4y-2=0与直线l2:2x-5y+b=0互相垂直,垂足为(1,c),则a+b+c的值为( )
A.-4 B.20
C.0 D.24
5.若直线x+(1+m)y-2=0与直线mx+2y+4=0平行,则m的值是( )
A.1 B.-2
C.1或-2 D.-
6.若方程x2+y2+kx+2y+k2=0所表示的圆取得最大面积,则直线y=(k-1)x+2的倾斜角α等于( )
A.45° B.135°
C.60° D.120°
7.将直线2x-y+λ=0沿x轴向左平移1个单位长度,所得直线与圆x2+y2+2x-4y=0相切,则实数λ的值为( )
A.-3或7 B.-2或8
C.0或10 D.1或11
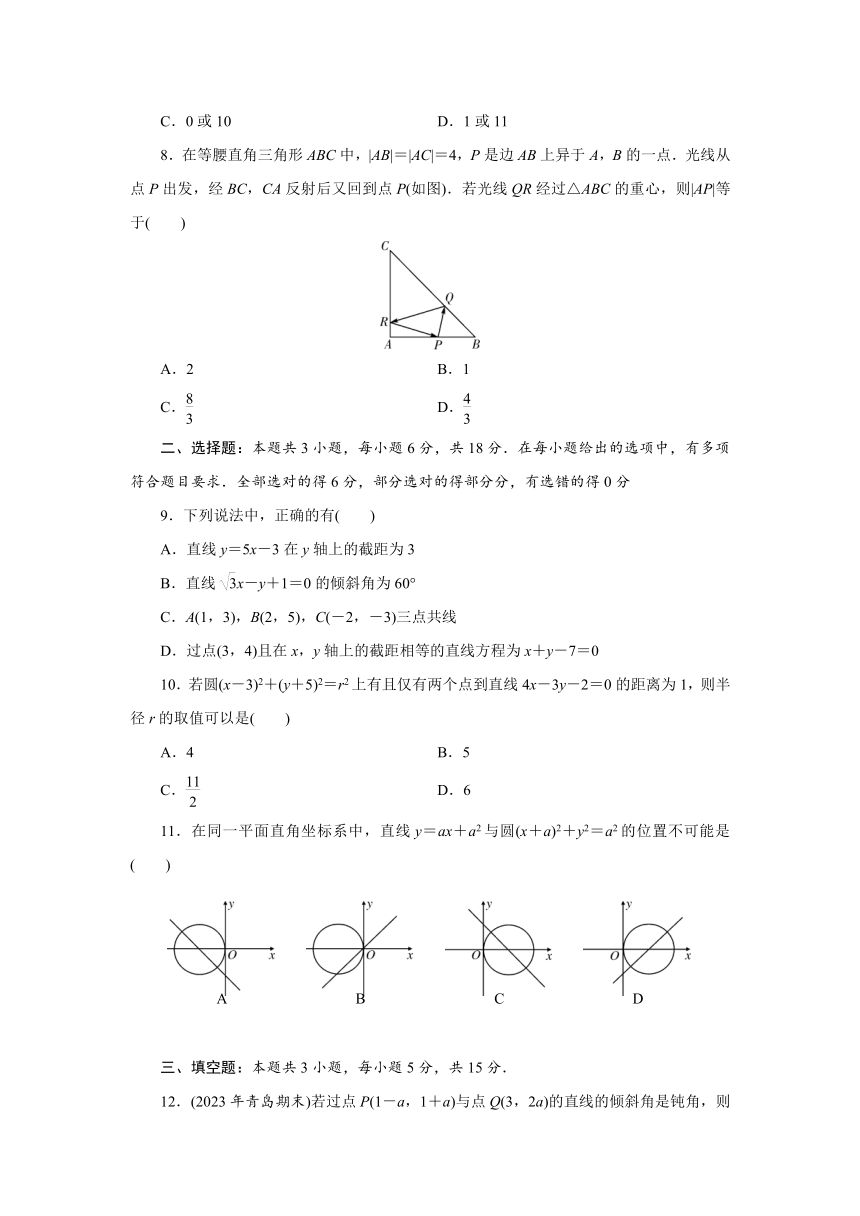
8.在等腰直角三角形ABC中,|AB|=|AC|=4,P是边AB上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则|AP|等于( )
A.2 B.1
C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分
9.下列说法中,正确的有( )
A.直线y=5x-3在y轴上的截距为3
B.直线x-y+1=0的倾斜角为60°
C.A(1,3),B(2,5),C(-2,-3)三点共线
D.过点(3,4)且在x,y轴上的截距相等的直线方程为x+y-7=0
10.若圆(x-3)2+(y+5)2=r2上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值可以是( )
A.4 B.5
C. D.6
11.在同一平面直角坐标系中,直线y=ax+a2与圆(x+a)2+y2=a2的位置不可能是( )
三、填空题:本题共3小题,每小题5分,共15分.
12.(2023年青岛期末)若过点P(1-a,1+a)与点Q(3,2a)的直线的倾斜角是钝角,则实数a的取值范围是________.
13.平面内动点P到两点A,B距离之比为常数λ(λ>0,且λ≠1),则动点P的轨迹叫做阿波罗尼斯圆,若已知A(-2,0),B(2,0),λ=,则此阿波罗尼斯圆的方程为__________.
14.已知圆O:x2+y2=1,l为过点(0,2)的动直线,若l与圆O相切,则直线l的倾斜角为________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知直线l经过两条直线l1:x+y-4=0和l2:x-y+2=0的交点,直线l3:2x-y-1=0.
(1)若l∥l3,求l的直线方程;
(2)若l⊥l3,求l的直线方程.
16.(15分)已知△ABC的三个顶点是A(-1,4),B(-2,-1),C(2,3).
(1)求BC边的高所在的直线方程;
(2)求△ABC的面积S.
17.(15分)已知半径为5的圆的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y-29=0相切.
(1)求圆的方程.
(2)若直线ax-y+5=0(a≠0)与圆相交于A,B两点,是否存在实数a,使得过点P(-2,4)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
18.(17分)已知△ABC的顶点C(2,-8),直线AB的方程为y=-2x+11,AC边上的高BH所在直线的方程为x+3y+2=0.
(1)求顶点A和B的坐标;
(2)求△ABC外接圆的一般方程.
19.(17分)已知直线l:2x-3y+1=0,点A(-1,-2).
(1)求点A关于直线l的对称点B的坐标;
(2)直线l关于点A对称的直线a的方程;
(3)以点A为圆心,3为半径长作圆,直线b过点M(2,2),且被圆A截得的弦长为2,求直线b的方程.
答案解析
1、【答案】A
【解析】2x-2y+1=0,则斜率k=1,设倾斜角是α,0≤α<π,即tan α=1,所以α=.故选A.
2、【答案】C
【解析】将圆的一般方程化为标准方程得C1:(x+1)2+(y+4)2=25,C2:(x-2)2+(y-2)2=9,所以C1(-1,-4),C2(2,2),r1=5,r2=3.从而|C1C2|==3,所以r1-r2<|C1C2|<r1+r2.因此两圆的位置关系为相交.故选C.
3、【答案】A
【解析】圆C:x2+y2+6x-8y+24=0化为标准方程为(x+3)2+(y-4)2=1,所以圆C的圆心为(-3,4),半径为1.因为点(-3,4)关于直线y=x的对称点为(4,-3),所以圆C关于直线y=x对称的圆的方程为(x-4)2+(y+3)2=1.故选A.
4、【答案】A
【解析】∵l1⊥l2,∴-·=-1,∴a=10.∴l1:10x+4y-2=0.将(1,c)代入,得10+4c-2=0,∴c=-2;将(1,-2)代入直线l2的方程,得2-5×(-2)+b=0,∴b=-12.故a+b+c=10+(-12)+(-2)=-4.
5、【答案】A
【解析】①当m=-1时,两直线分别为x-2=0和x-2y-4=0,此时两直线相交,不合题意.
②当m≠-1时,两直线的斜率都存在,由直线平行可得解得m=1.综上可得m=1.故选A.
6、【答案】B
【解析】将圆x2+y2+kx+2y+k2=0化成标准方程,得+(y+1)2=1-,所以r2=1-,当圆取得最大面积时,k=0,半径r=1,因此直线y=(k-1)x+2,即y=-x+2,则直线的倾斜角α满足tan α=-1,所以α=135°.故选B.
7、【答案】A
【解析】由题意知,直线2x-y+λ=0平移后方程为2(x+1)-y+λ=0,圆x2+y2+2x-4y=0的圆心坐标为(-1,2),半径为.直线与圆相切,则圆心到直线的距离等于圆的半径,因而有=,解得λ=-3或λ=7.
8、【答案】D
【解析】以A为坐标原点,AB所在直线为x轴,AC所在直线为y轴建立如图所示的平面直角坐标系.由题可知B(4,0),C(0,4),A(0,0),则直线BC的方程为x+y-4=0.设P(t,0)(0<t<4),由对称知识可得点P关于直线BC的对称点P1的坐标为(4,4-t),点P关于y轴的对称点P2的坐标为(-t,0),根据反射定理可知P1P2就是光线RQ所在直线.由P1,P2两点的坐标可得直线P1P2的方程为y=(x+t).设△ABC的重心为G,易知G.因为重心G在光线RQ上,所以有=·,即3t2-4t=0,解得t=0或t=.因为0<t<4,所以t=,即|AP|=.故选D.
9、【答案】BC
【解析】对于A,直线y=5x-3在y轴上的截距为-3,故A错误;对于B,x-y+1=0 y=x+1,所以直线的斜率为k=tan α=,则倾斜角α=60°,故B正确;对于C,由A(1,3),B(2,5),C(-2,-3)可得=(1,2),=(-4,-8),所以=-,A,B,C三点共线,故C正确;对于D,过点(3,4)且在x,y轴上的截距相等的直线方程为x+y-7=0或y=x,故D错误.故选BC.
10、【答案】BC
【解析】易求圆心(3,-5),到直线4x-3y-2=0的距离d=5,由已知得d-1<r<d+1,即4<r<6.故选BC.
11、【答案】ABD
【解析】直线y=ax+a2经过圆(x+a)2+y2=a2的圆心(-a,0),且斜率为a,故不可能为A,B,D.
12、【答案】(-2,1)
【解析】设直线的斜率为k,则k==<0,得-2<a<1.
13、【答案】x2+y2+x+4=0
【解析】由题意,设P(x,y),则=,化简可得x2+y2+x+4=0.
14、【答案】或
【解析】若直线l与圆相切,则l的斜率肯定存在,设l:y=kx+2,则d==1,所以k=±.所以直线l的倾斜角为或.
15、解:(1)由得
∴l1与l2的交点为(1,3).
设与直线2x-y-1=0平行的直线为2x-y+c=0,
则2-3+c=0,
∴c=1.
∴所求直线方程为2x-y+1=0.
(2)设与直线2x-y-1=0垂直的直线为x+2y+c=0,
则1+2×3+c=0,解得c=-7.
∴所求直线方程为x+2y-7=0.
16、解:(1)设BC边的高所在直线为l,由题知
kBC==1,则kl==-1.
因为点A(-1,4)在直线l上,
所以直线l的方程为y-4=-1×(x+1),即x+y-3=0.
(2)BC所在直线方程为y+1=1×(x+2),即x-y+1=0,
点A(-1,4)到BC的距离d==2,
因为|BC|==4,则S△ABC=·|BC|·d=×4×2=8.
17、解:(1)设圆心为M(m,0)(m∈Z).
由于圆与直线4x+3y-29=0相切,且半径为5,
所以=5,即|4m-29|=25,解得m=或m=1.
因为m为整数,故m=1,
所以所求圆的方程是(x-1)2+y2=25.
(2)假设符合条件的实数a存在,
因为a≠0,则直线l的斜率为-,l的方程为y=-(x+2)+4,即x+ay+2-4a=0.
由于l垂直平分弦AB,故圆心M(1,0)必在l上.
所以1+0+2-4a=0,解得a=.
经检验,当a=时,直线ax-y+5=0与圆有两个交点.
故存在实数a=,使得过点P(-2,4)的直线l垂直平分弦AB.
18、解:(1)由得顶点B(7,-3).
由AC⊥BH,kBH=-.所以可设AC的方程为y=3x+b,
将C(2,-8)代入,得b=-14.
由得顶点为A(5,1).
所以点A和B的坐标分别为(5,1)和(7,-3).
(2)设△ABC的外接圆方程为x2+y2+Dx+Ey+F=0,
将点A(5,1),B(7,-3),C(2,-8)分别代入圆的方程,
得解得
所以△ABC的外接圆的一般方程为x2+y2-4x+6y-12=0.
19、解:(1)设点B(m,n),
则
解得
所以点A关于直线l的对称点B的坐标为.
(2)设P(x,y)是直线a上任意一点,
则点P(x,y)关于点A(-1,-2)的对称点C(-2-x,-4-y)在直线l上,
所以2(-2-x)-3(-4-y)+1=0,即2x-3y-9=0.
(3)设圆心A到直线b的距离为d,直线b被圆A截得的弦长为2,因此d==.
当直线b斜率不存在时,x=2不满足条件;
当直线b斜率存在时,设其方程为y-2=k(x-2),则=,解得k=.
综上,直线b的方程为y=x-或y=x-.
章末检测
(时间:120分钟,满分150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线2x-2y+1=0的倾斜角是( )
A. B.
C. D.
2.圆C1:x2+y2+2x+8y-8=0与圆C2:x2+y2-4x-4y-1=0的位置关系是( )
A.外离 B.外切
C.相交 D.内含
3.圆C:x2+y2+6x-8y+24=0关于直线y=x对称的圆的方程为( )
A.(x-4)2+(y+3)2=1 B.(x-4)2+(y-3)2=49
C.(x+4)2+(y-3)2=1 D.(x+4)2+(y+3)2=49
4.已知直线l1:ax+4y-2=0与直线l2:2x-5y+b=0互相垂直,垂足为(1,c),则a+b+c的值为( )
A.-4 B.20
C.0 D.24
5.若直线x+(1+m)y-2=0与直线mx+2y+4=0平行,则m的值是( )
A.1 B.-2
C.1或-2 D.-
6.若方程x2+y2+kx+2y+k2=0所表示的圆取得最大面积,则直线y=(k-1)x+2的倾斜角α等于( )
A.45° B.135°
C.60° D.120°
7.将直线2x-y+λ=0沿x轴向左平移1个单位长度,所得直线与圆x2+y2+2x-4y=0相切,则实数λ的值为( )
A.-3或7 B.-2或8
C.0或10 D.1或11
8.在等腰直角三角形ABC中,|AB|=|AC|=4,P是边AB上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则|AP|等于( )
A.2 B.1
C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分
9.下列说法中,正确的有( )
A.直线y=5x-3在y轴上的截距为3
B.直线x-y+1=0的倾斜角为60°
C.A(1,3),B(2,5),C(-2,-3)三点共线
D.过点(3,4)且在x,y轴上的截距相等的直线方程为x+y-7=0
10.若圆(x-3)2+(y+5)2=r2上有且仅有两个点到直线4x-3y-2=0的距离为1,则半径r的取值可以是( )
A.4 B.5
C. D.6
11.在同一平面直角坐标系中,直线y=ax+a2与圆(x+a)2+y2=a2的位置不可能是( )
三、填空题:本题共3小题,每小题5分,共15分.
12.(2023年青岛期末)若过点P(1-a,1+a)与点Q(3,2a)的直线的倾斜角是钝角,则实数a的取值范围是________.
13.平面内动点P到两点A,B距离之比为常数λ(λ>0,且λ≠1),则动点P的轨迹叫做阿波罗尼斯圆,若已知A(-2,0),B(2,0),λ=,则此阿波罗尼斯圆的方程为__________.
14.已知圆O:x2+y2=1,l为过点(0,2)的动直线,若l与圆O相切,则直线l的倾斜角为________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知直线l经过两条直线l1:x+y-4=0和l2:x-y+2=0的交点,直线l3:2x-y-1=0.
(1)若l∥l3,求l的直线方程;
(2)若l⊥l3,求l的直线方程.
16.(15分)已知△ABC的三个顶点是A(-1,4),B(-2,-1),C(2,3).
(1)求BC边的高所在的直线方程;
(2)求△ABC的面积S.
17.(15分)已知半径为5的圆的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y-29=0相切.
(1)求圆的方程.
(2)若直线ax-y+5=0(a≠0)与圆相交于A,B两点,是否存在实数a,使得过点P(-2,4)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
18.(17分)已知△ABC的顶点C(2,-8),直线AB的方程为y=-2x+11,AC边上的高BH所在直线的方程为x+3y+2=0.
(1)求顶点A和B的坐标;
(2)求△ABC外接圆的一般方程.
19.(17分)已知直线l:2x-3y+1=0,点A(-1,-2).
(1)求点A关于直线l的对称点B的坐标;
(2)直线l关于点A对称的直线a的方程;
(3)以点A为圆心,3为半径长作圆,直线b过点M(2,2),且被圆A截得的弦长为2,求直线b的方程.
答案解析
1、【答案】A
【解析】2x-2y+1=0,则斜率k=1,设倾斜角是α,0≤α<π,即tan α=1,所以α=.故选A.
2、【答案】C
【解析】将圆的一般方程化为标准方程得C1:(x+1)2+(y+4)2=25,C2:(x-2)2+(y-2)2=9,所以C1(-1,-4),C2(2,2),r1=5,r2=3.从而|C1C2|==3,所以r1-r2<|C1C2|<r1+r2.因此两圆的位置关系为相交.故选C.
3、【答案】A
【解析】圆C:x2+y2+6x-8y+24=0化为标准方程为(x+3)2+(y-4)2=1,所以圆C的圆心为(-3,4),半径为1.因为点(-3,4)关于直线y=x的对称点为(4,-3),所以圆C关于直线y=x对称的圆的方程为(x-4)2+(y+3)2=1.故选A.
4、【答案】A
【解析】∵l1⊥l2,∴-·=-1,∴a=10.∴l1:10x+4y-2=0.将(1,c)代入,得10+4c-2=0,∴c=-2;将(1,-2)代入直线l2的方程,得2-5×(-2)+b=0,∴b=-12.故a+b+c=10+(-12)+(-2)=-4.
5、【答案】A
【解析】①当m=-1时,两直线分别为x-2=0和x-2y-4=0,此时两直线相交,不合题意.
②当m≠-1时,两直线的斜率都存在,由直线平行可得解得m=1.综上可得m=1.故选A.
6、【答案】B
【解析】将圆x2+y2+kx+2y+k2=0化成标准方程,得+(y+1)2=1-,所以r2=1-,当圆取得最大面积时,k=0,半径r=1,因此直线y=(k-1)x+2,即y=-x+2,则直线的倾斜角α满足tan α=-1,所以α=135°.故选B.
7、【答案】A
【解析】由题意知,直线2x-y+λ=0平移后方程为2(x+1)-y+λ=0,圆x2+y2+2x-4y=0的圆心坐标为(-1,2),半径为.直线与圆相切,则圆心到直线的距离等于圆的半径,因而有=,解得λ=-3或λ=7.
8、【答案】D
【解析】以A为坐标原点,AB所在直线为x轴,AC所在直线为y轴建立如图所示的平面直角坐标系.由题可知B(4,0),C(0,4),A(0,0),则直线BC的方程为x+y-4=0.设P(t,0)(0<t<4),由对称知识可得点P关于直线BC的对称点P1的坐标为(4,4-t),点P关于y轴的对称点P2的坐标为(-t,0),根据反射定理可知P1P2就是光线RQ所在直线.由P1,P2两点的坐标可得直线P1P2的方程为y=(x+t).设△ABC的重心为G,易知G.因为重心G在光线RQ上,所以有=·,即3t2-4t=0,解得t=0或t=.因为0<t<4,所以t=,即|AP|=.故选D.
9、【答案】BC
【解析】对于A,直线y=5x-3在y轴上的截距为-3,故A错误;对于B,x-y+1=0 y=x+1,所以直线的斜率为k=tan α=,则倾斜角α=60°,故B正确;对于C,由A(1,3),B(2,5),C(-2,-3)可得=(1,2),=(-4,-8),所以=-,A,B,C三点共线,故C正确;对于D,过点(3,4)且在x,y轴上的截距相等的直线方程为x+y-7=0或y=x,故D错误.故选BC.
10、【答案】BC
【解析】易求圆心(3,-5),到直线4x-3y-2=0的距离d=5,由已知得d-1<r<d+1,即4<r<6.故选BC.
11、【答案】ABD
【解析】直线y=ax+a2经过圆(x+a)2+y2=a2的圆心(-a,0),且斜率为a,故不可能为A,B,D.
12、【答案】(-2,1)
【解析】设直线的斜率为k,则k==<0,得-2<a<1.
13、【答案】x2+y2+x+4=0
【解析】由题意,设P(x,y),则=,化简可得x2+y2+x+4=0.
14、【答案】或
【解析】若直线l与圆相切,则l的斜率肯定存在,设l:y=kx+2,则d==1,所以k=±.所以直线l的倾斜角为或.
15、解:(1)由得
∴l1与l2的交点为(1,3).
设与直线2x-y-1=0平行的直线为2x-y+c=0,
则2-3+c=0,
∴c=1.
∴所求直线方程为2x-y+1=0.
(2)设与直线2x-y-1=0垂直的直线为x+2y+c=0,
则1+2×3+c=0,解得c=-7.
∴所求直线方程为x+2y-7=0.
16、解:(1)设BC边的高所在直线为l,由题知
kBC==1,则kl==-1.
因为点A(-1,4)在直线l上,
所以直线l的方程为y-4=-1×(x+1),即x+y-3=0.
(2)BC所在直线方程为y+1=1×(x+2),即x-y+1=0,
点A(-1,4)到BC的距离d==2,
因为|BC|==4,则S△ABC=·|BC|·d=×4×2=8.
17、解:(1)设圆心为M(m,0)(m∈Z).
由于圆与直线4x+3y-29=0相切,且半径为5,
所以=5,即|4m-29|=25,解得m=或m=1.
因为m为整数,故m=1,
所以所求圆的方程是(x-1)2+y2=25.
(2)假设符合条件的实数a存在,
因为a≠0,则直线l的斜率为-,l的方程为y=-(x+2)+4,即x+ay+2-4a=0.
由于l垂直平分弦AB,故圆心M(1,0)必在l上.
所以1+0+2-4a=0,解得a=.
经检验,当a=时,直线ax-y+5=0与圆有两个交点.
故存在实数a=,使得过点P(-2,4)的直线l垂直平分弦AB.
18、解:(1)由得顶点B(7,-3).
由AC⊥BH,kBH=-.所以可设AC的方程为y=3x+b,
将C(2,-8)代入,得b=-14.
由得顶点为A(5,1).
所以点A和B的坐标分别为(5,1)和(7,-3).
(2)设△ABC的外接圆方程为x2+y2+Dx+Ey+F=0,
将点A(5,1),B(7,-3),C(2,-8)分别代入圆的方程,
得解得
所以△ABC的外接圆的一般方程为x2+y2-4x+6y-12=0.
19、解:(1)设点B(m,n),
则
解得
所以点A关于直线l的对称点B的坐标为.
(2)设P(x,y)是直线a上任意一点,
则点P(x,y)关于点A(-1,-2)的对称点C(-2-x,-4-y)在直线l上,
所以2(-2-x)-3(-4-y)+1=0,即2x-3y-9=0.
(3)设圆心A到直线b的距离为d,直线b被圆A截得的弦长为2,因此d==.
当直线b斜率不存在时,x=2不满足条件;
当直线b斜率存在时,设其方程为y-2=k(x-2),则=,解得k=.
综上,直线b的方程为y=x-或y=x-.
