人教版 必修第一册 3.4.1 力的合成 课件(共34张PPT)
文档属性
| 名称 | 人教版 必修第一册 3.4.1 力的合成 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-22 19:59:30 | ||
图片预览









文档简介
(共34张PPT)
4 力的合成
第三章 相互作用
[学习目标]
1.理解合力,分力,力的合成的概念
2..掌握平行四边形定则,会用平行四边形定则求合力
等效替代
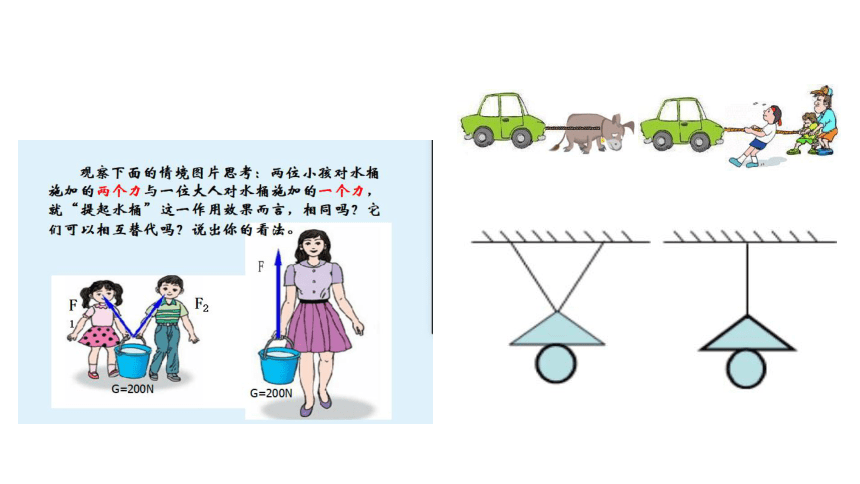
假设一个力单独作用的效果跟某几个力共同作用的效果相同,这个力就叫做那几个力的合力(resultant force)。
假设几个力共同作用的效果跟某个力单独作用的效果相同,这几个力就叫作那个力的分力(component force)。
合力与分力
(1)等效性:合力的作用效果与分力的共同作用效果相同,它们在效果上可以相互替代。
(2)同体性:各个分力是作用在同一物体上的,分力与合力为同一物体,作用在不同物体上的力不能求合力。
(3)瞬时性:各个分力与合力具有瞬时对应关系,某个分力变化了,合力也同时发生变化。
合力与分力的关系
02
思(3min)
通读课本第三章第四节P72-P73的内容,用笔勾画概念、定义、公式等。
填写优化设计75、82页。
同向相加反向相减
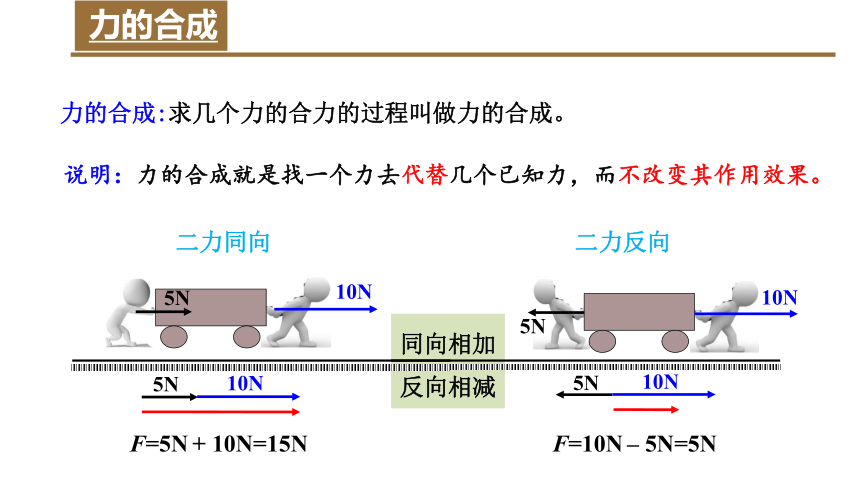
力的合成:求几个力的合力的过程叫做力的合成。
说明:力的合成就是找一个力去代替几个已知力,而不改变其作用效果。
二力同向
10N
5N
10N
5N
二力反向
5N
10N
10N
F=5N + 10N=15N
F=10N – 5N=5N
5N
力的合成
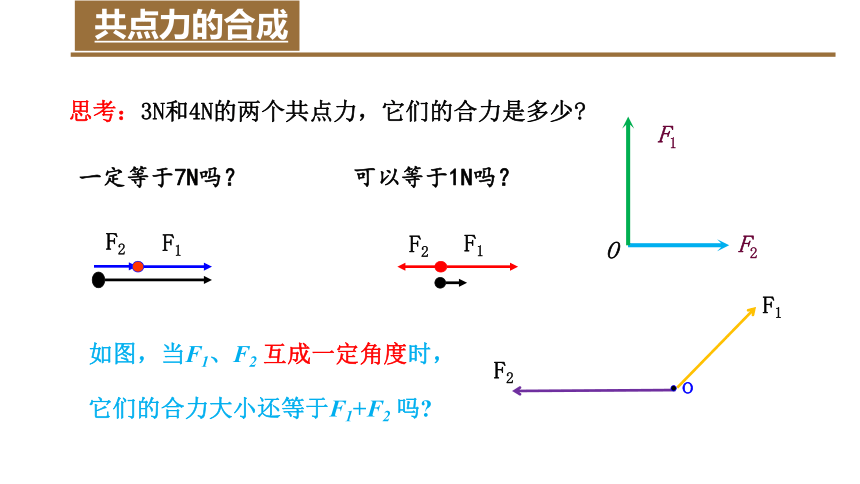
思考:3N和4N的两个共点力,它们的合力是多少
一定等于7N吗?
可以等于1N吗?
F2
F1
F2
F1
F1
F2
o
O
F2
F1
如图,当F1、F2 互成一定角度时,它们的合力大小还等于F1+F2 吗
共点力的合成
二,探究力的合成规律
4.互成角度力的合成——实验
(1)实验原理:根据 的思想,将橡皮条的一端固定,另一端用两个力 和 使其到达某一点,再用一个力F作用于橡皮条的同一点,使其到达同一点,那么F与 、 的作用效果相同;记下 和 的大小和方向,画出力的图示,研究F与 、 的关系。
(2)实验步骤:(阅读课本62页“实验”)
等效替代
二,探究力的合成规律
(3)实验结论:力的合成遵循的法则—— ;
方法:两个力合成时,以表示这两个力的线段为 作平行四边形,这两个邻边之间的 就代表合力的大小和方向。
5.多个力合成的方法
先求出 的合力,再求出这个合力与 的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力。
平行四边形定则
邻边
对角线
任意两个力
第三个力
(1)在桌面上固定一个贴有白纸的方木板,用图钉把橡皮筋的一端固定在板上靠近顶端中点的A点,在橡皮筋的另外一端拴上两条细绳,细绳的另外一端是绳套。
A
5、实验步骤
O
(2)用弹簧秤分别钩住绳套,互成角度地拉橡皮筋,使橡皮筋伸长,结点达到某一位置O。
(3)用铅笔从O点沿着两绳的方向画直线,作出两个力F1和F2的图示。
A
O
(4)只用一只弹簧秤,通过细绳把橡皮筋的结点拉到相同的位置O点,读出弹簧秤的示数,记下细绳的方向,作出这个力F的图示。研究这三个力的大小及方向的关系。
6、实验结论
F2
F
·
F1
O
实验表明,在两个力合成时,以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向。这个规律叫作平行四边形定则。
两个力的合成
注意:作图要准确,两个分力F1、F2和合力F要画成实线并标有箭头,平行四边形的另外两条平行线必须画成虚线。
三、探究力的合成规律
1.平行四边形定则的适用范围。
2.分析合力与分力的大小关系。
共点力
当两分力 、 大小一定,夹角 从0度增大到180度时,合力大小随夹角 的增大而减小。
(1)最大值:夹角 (两力同向)时合力最大, = ,方向与两力同向;
(2)最小值:夹角 (两力反向)时合力最小, = ,方向与两力中较大的力相向;
(3)合力范围:
1.判断下列说法的正误.
(1)合力与原来那几个力同时作用在物体上.( )
(2)合力的作用可以替代原来那几个力的作用,它与那几个力是等效替代关系.( )
(3)合力总比分力大.( )
(4)作用在一个物体上的两个力,如果大小相等,方向相反,则这两个力一定是共点力.( )
[即学即用]
×
√
×
×
答案
2.两个共点力互相垂直,F1=8 N,F2=6 N,则它们的合力F=____ N,合力与F1间的夹角θ=____.
10
37°
解析:
(1)合力与原来几个力是等效替代关系,不是同时作用在物体上。故错误;
(2)合力的作用可以替代原来几个力的作用,它与那几个力是等效替代关系。故正确;
(3)根据平行四边形定则,合力可能大于、等于或小于分力。故错误;
(4)作用在一个物体上的两个力,如果大小相等,方向相反,但这两个力不是作用在同一点或其作用线的延长线交于一点,则不是共点力。故错误。
一、合力与分力的关系
[知识深化]
1.合力与分力的三性
①互成角度的二个共点力如果保持大小不变,它们的合力将随夹角的增大而减小;
②合力有可能大于或小于或等于任何一个分力。
③ F1、F2同向合力最大,反向合力最小。
④合力大小范围:︱F1 - F2︱ ≤ F ≤ F1 + F2
针对训练1 如图7所示,两个人共同用力将一个牌匾拉上墙头.其中一人用了450 N的拉力,另一个人用了600 N的拉力,如果这两个人所用拉力的夹角是90°,求它们的合力.(已知sin 53°=0.8,cos 53°=0.6)
答案
解析
图7
答案 750 N,方向与较小拉力的夹角为53°
图3
图4
图5
若α=120°,则合力大小等于分力大小(如图5所示).
③合力与一个分力垂直: , 方向与 方向的夹角成直角
课堂检测
1.(合力大小与夹角的关系)关于两个大小不变的共点力F1、F2与其合力F的关系,下列说法中正确的是
A.F大小随F1、F2间夹角的增大而增大(夹角小于180°时)
B.F大小随F1、F2间夹角的增大而减小(夹角小于180°时)
C.F大小一定小于F1、F2中最大者
D.F大小不能小于F1、F2中最小
√
答案
1
2
3
4
解析
5
解析:
合力随两分力间夹角的增大而减小,合力大小的范围为|F1-F |≤F≤F1+F 。例如,当F1=5 N、F =6 N时,1N≤ F≤11 N,F 可比 F1、F 中的最小者小,也可以比F1、F2中的最大者大,故只有选项B正确。
2.(合力大小范围)两个共点力的大小分别为F1=15 N,F2=8 N,它们的合力大小不可能等于
A.9 N B.25 N
C.8 N D.21 N
√
解析 F1、F2的合力范围是|F1-F2|≤F≤F1+F2,故7 N≤F≤23 N,不在此范围的是25 N,应选择B项.
3.(两个力的合成)有两个大小相等的共点力F1和F2,当它们的夹角为90°时,合力为F,它们的夹角变为120°时,合力的大小为
√
4.(两个力的合成)如图10所示,水平地面上固定着一根竖直立柱,某人用绳子通过柱顶的光滑定滑轮将100 N的货物拉住.已知人拉着绳子的一端,且该绳端与水平方向夹角为30°,则柱顶所受压力大小为
图10
√
解析 如图所示,
定滑轮只改变力的方向,不改变力的大小,
所以绳的拉力F1=F2=100 N,
柱顶所受压力大小
5.(多个力的合成)如图所示,三个大小相等的力F,作用于同一点O,则合力最小的是
√
解析
1、本题是关于力的合成的题目,解题时要掌握力的合成的平行四边形定则;
2、对于三个力的合成,通常可先将其中任意两个力合成,再将此合力与第三个力合成;
3、分析各个选项,求出其合力的大小。例如A,可先将两互相垂直的力合成:F合A1=√2F,再将此合力与斜向上的力合成F合A=(√2-1)F,最后比较各个选项中合力的大小即可得出正确答案C.
4 力的合成
第三章 相互作用
[学习目标]
1.理解合力,分力,力的合成的概念
2..掌握平行四边形定则,会用平行四边形定则求合力
等效替代
假设一个力单独作用的效果跟某几个力共同作用的效果相同,这个力就叫做那几个力的合力(resultant force)。
假设几个力共同作用的效果跟某个力单独作用的效果相同,这几个力就叫作那个力的分力(component force)。
合力与分力
(1)等效性:合力的作用效果与分力的共同作用效果相同,它们在效果上可以相互替代。
(2)同体性:各个分力是作用在同一物体上的,分力与合力为同一物体,作用在不同物体上的力不能求合力。
(3)瞬时性:各个分力与合力具有瞬时对应关系,某个分力变化了,合力也同时发生变化。
合力与分力的关系
02
思(3min)
通读课本第三章第四节P72-P73的内容,用笔勾画概念、定义、公式等。
填写优化设计75、82页。
同向相加反向相减
力的合成:求几个力的合力的过程叫做力的合成。
说明:力的合成就是找一个力去代替几个已知力,而不改变其作用效果。
二力同向
10N
5N
10N
5N
二力反向
5N
10N
10N
F=5N + 10N=15N
F=10N – 5N=5N
5N
力的合成
思考:3N和4N的两个共点力,它们的合力是多少
一定等于7N吗?
可以等于1N吗?
F2
F1
F2
F1
F1
F2
o
O
F2
F1
如图,当F1、F2 互成一定角度时,它们的合力大小还等于F1+F2 吗
共点力的合成
二,探究力的合成规律
4.互成角度力的合成——实验
(1)实验原理:根据 的思想,将橡皮条的一端固定,另一端用两个力 和 使其到达某一点,再用一个力F作用于橡皮条的同一点,使其到达同一点,那么F与 、 的作用效果相同;记下 和 的大小和方向,画出力的图示,研究F与 、 的关系。
(2)实验步骤:(阅读课本62页“实验”)
等效替代
二,探究力的合成规律
(3)实验结论:力的合成遵循的法则—— ;
方法:两个力合成时,以表示这两个力的线段为 作平行四边形,这两个邻边之间的 就代表合力的大小和方向。
5.多个力合成的方法
先求出 的合力,再求出这个合力与 的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力。
平行四边形定则
邻边
对角线
任意两个力
第三个力
(1)在桌面上固定一个贴有白纸的方木板,用图钉把橡皮筋的一端固定在板上靠近顶端中点的A点,在橡皮筋的另外一端拴上两条细绳,细绳的另外一端是绳套。
A
5、实验步骤
O
(2)用弹簧秤分别钩住绳套,互成角度地拉橡皮筋,使橡皮筋伸长,结点达到某一位置O。
(3)用铅笔从O点沿着两绳的方向画直线,作出两个力F1和F2的图示。
A
O
(4)只用一只弹簧秤,通过细绳把橡皮筋的结点拉到相同的位置O点,读出弹簧秤的示数,记下细绳的方向,作出这个力F的图示。研究这三个力的大小及方向的关系。
6、实验结论
F2
F
·
F1
O
实验表明,在两个力合成时,以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向。这个规律叫作平行四边形定则。
两个力的合成
注意:作图要准确,两个分力F1、F2和合力F要画成实线并标有箭头,平行四边形的另外两条平行线必须画成虚线。
三、探究力的合成规律
1.平行四边形定则的适用范围。
2.分析合力与分力的大小关系。
共点力
当两分力 、 大小一定,夹角 从0度增大到180度时,合力大小随夹角 的增大而减小。
(1)最大值:夹角 (两力同向)时合力最大, = ,方向与两力同向;
(2)最小值:夹角 (两力反向)时合力最小, = ,方向与两力中较大的力相向;
(3)合力范围:
1.判断下列说法的正误.
(1)合力与原来那几个力同时作用在物体上.( )
(2)合力的作用可以替代原来那几个力的作用,它与那几个力是等效替代关系.( )
(3)合力总比分力大.( )
(4)作用在一个物体上的两个力,如果大小相等,方向相反,则这两个力一定是共点力.( )
[即学即用]
×
√
×
×
答案
2.两个共点力互相垂直,F1=8 N,F2=6 N,则它们的合力F=____ N,合力与F1间的夹角θ=____.
10
37°
解析:
(1)合力与原来几个力是等效替代关系,不是同时作用在物体上。故错误;
(2)合力的作用可以替代原来几个力的作用,它与那几个力是等效替代关系。故正确;
(3)根据平行四边形定则,合力可能大于、等于或小于分力。故错误;
(4)作用在一个物体上的两个力,如果大小相等,方向相反,但这两个力不是作用在同一点或其作用线的延长线交于一点,则不是共点力。故错误。
一、合力与分力的关系
[知识深化]
1.合力与分力的三性
①互成角度的二个共点力如果保持大小不变,它们的合力将随夹角的增大而减小;
②合力有可能大于或小于或等于任何一个分力。
③ F1、F2同向合力最大,反向合力最小。
④合力大小范围:︱F1 - F2︱ ≤ F ≤ F1 + F2
针对训练1 如图7所示,两个人共同用力将一个牌匾拉上墙头.其中一人用了450 N的拉力,另一个人用了600 N的拉力,如果这两个人所用拉力的夹角是90°,求它们的合力.(已知sin 53°=0.8,cos 53°=0.6)
答案
解析
图7
答案 750 N,方向与较小拉力的夹角为53°
图3
图4
图5
若α=120°,则合力大小等于分力大小(如图5所示).
③合力与一个分力垂直: , 方向与 方向的夹角成直角
课堂检测
1.(合力大小与夹角的关系)关于两个大小不变的共点力F1、F2与其合力F的关系,下列说法中正确的是
A.F大小随F1、F2间夹角的增大而增大(夹角小于180°时)
B.F大小随F1、F2间夹角的增大而减小(夹角小于180°时)
C.F大小一定小于F1、F2中最大者
D.F大小不能小于F1、F2中最小
√
答案
1
2
3
4
解析
5
解析:
合力随两分力间夹角的增大而减小,合力大小的范围为|F1-F |≤F≤F1+F 。例如,当F1=5 N、F =6 N时,1N≤ F≤11 N,F 可比 F1、F 中的最小者小,也可以比F1、F2中的最大者大,故只有选项B正确。
2.(合力大小范围)两个共点力的大小分别为F1=15 N,F2=8 N,它们的合力大小不可能等于
A.9 N B.25 N
C.8 N D.21 N
√
解析 F1、F2的合力范围是|F1-F2|≤F≤F1+F2,故7 N≤F≤23 N,不在此范围的是25 N,应选择B项.
3.(两个力的合成)有两个大小相等的共点力F1和F2,当它们的夹角为90°时,合力为F,它们的夹角变为120°时,合力的大小为
√
4.(两个力的合成)如图10所示,水平地面上固定着一根竖直立柱,某人用绳子通过柱顶的光滑定滑轮将100 N的货物拉住.已知人拉着绳子的一端,且该绳端与水平方向夹角为30°,则柱顶所受压力大小为
图10
√
解析 如图所示,
定滑轮只改变力的方向,不改变力的大小,
所以绳的拉力F1=F2=100 N,
柱顶所受压力大小
5.(多个力的合成)如图所示,三个大小相等的力F,作用于同一点O,则合力最小的是
√
解析
1、本题是关于力的合成的题目,解题时要掌握力的合成的平行四边形定则;
2、对于三个力的合成,通常可先将其中任意两个力合成,再将此合力与第三个力合成;
3、分析各个选项,求出其合力的大小。例如A,可先将两互相垂直的力合成:F合A1=√2F,再将此合力与斜向上的力合成F合A=(√2-1)F,最后比较各个选项中合力的大小即可得出正确答案C.
