14.3.2 第1课时 运用平方差公式因式分解 课件(共15张PPT) 人教版数学八年级上册
文档属性
| 名称 | 14.3.2 第1课时 运用平方差公式因式分解 课件(共15张PPT) 人教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-23 21:39:32 | ||
图片预览





文档简介
(共15张PPT)
14.3.2 公式法
第十四章 整式的乘法与因式分解
第1课时 用平方差公式分解因式
14.3 因式分解
学习目标
1.经历利用平方差公式进行分解因式的过程,掌握利用平方差公式分解因式的方法(重点)
2. 能综合运用提公因式和平方差公式对多项式进行分解因式.(难点)
情景小游戏
小组竞猜:
已知 n 为整数,(2n + 1)2 - 25 能被3---9这
七个数字中的哪个数字整除?
平方差公式
导入新课
(a + b)(a - b) = a2 - b2
整式乘法
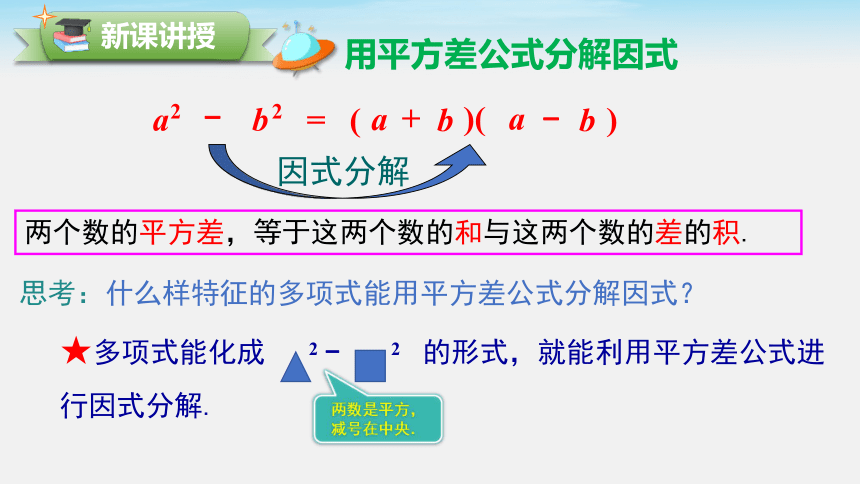
a2 - b2 = (a + b)(a - b)
因式分解
互逆变形
思考:什么样特征的多项式能用平方差公式分解因式?
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
因式分解
两个数的平方差,等于这两个数的和与这两个数的差的积.
用平方差公式分解因式
★多项式能化成 2 - 2 的形式,就能利用平方差公式进行因式分解.
注意:必须符合
2 - 2 的形式.
√
√
×
×
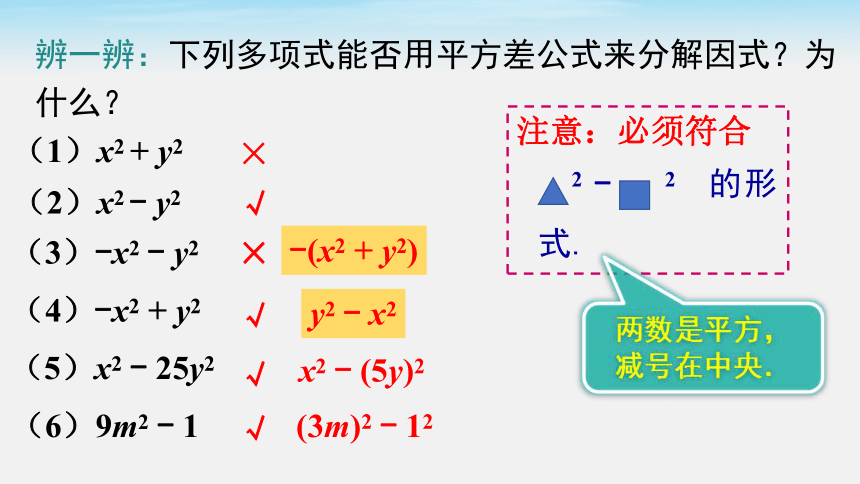
辨一辨:下列多项式能否用平方差公式来分解因式?为什么?
√
√
(1)x2 + y2
(2)x2 - y2
(3)-x2 - y2
-(x2 + y2)
y2 - x2
(4)-x2 + y2
(5)x2 - 25y2
x2 - (5y)2
(6)9m2 - 1
(3m)2 - 12
例1 分解因式:
解:(1) 原式 =
(2) 原式
典例精析
分解因式:
(1) a2- b2; (2) (a+b)2-4a2
针对训练
=(a+ b)(a- b)
(2) 原式=(a+b)2-(2a)2
=(3a+b)(b-a).
解:(1) 原式=a2-( b)2
=(a+b+2a)(a+b-2a)
例2 分解因式:
解:(1) 原式=( x2 )2 - ( y2 )2
=( x2 + y2 )( x2 - y2)
=(x2 + y2)(x + y)(x - y).
(2) 原式=ab(a2 - 1)
分解因式时,有公因式的一般先提公因式,然后再套用公式分解,最后进行检查
=ab(a + 1)(a - 1).
分解因式:
(1) 5a2m -5b2m; (2) 4y4-4.
针对训练
= 4(y2+1)(y+1)(y-1)
解:(1) 原式 = 5m(a2-b2)
= 5m(a+b)(a-b)
(2) 原式 = 4(y4-1)
= 4(y2+1)(y2-1)
例3 简便计算:
1012 - 992;
解:原式=(101+99)×(101-99)=400.
方法总结:较为复杂的有理数运算,可以运用因式分解对其进行变形,使运算得以简化.
=200×2
=400.
达标检测(每题25分,共100分):
(1) 16a2 - 9b2 = _________________;
(2) (广州中考) xy2 - 9x =_________________;
(3) (徐州中考)16-m4 =___________________;
(4) 53.52×4 - 46.52×4 =____________.
(4a + 3b)(4a - 3b)
x(y + 3)(y - 3)
(4 + m2)(2 + m)(2 - m)
2800
∵ n 为整数,
∴ (2n + 1)2 - 25 能被 4 整除.
已知 n 为整数,(2n + 1)2 - 25 能被 几整除?
解 :原式 = (2n + 1 + 5)(2n + 1 - 5)
= (2n + 6)(2n - 4)
= 2(n + 3)×2(n - 2) = 4(n + 3)(n - 2).
兑奖时刻:你猜对了吗?
书面 作业:
课本119页第2题、4题
谢 谢 聆 听
14.3.2 公式法
第十四章 整式的乘法与因式分解
第1课时 用平方差公式分解因式
14.3 因式分解
学习目标
1.经历利用平方差公式进行分解因式的过程,掌握利用平方差公式分解因式的方法(重点)
2. 能综合运用提公因式和平方差公式对多项式进行分解因式.(难点)
情景小游戏
小组竞猜:
已知 n 为整数,(2n + 1)2 - 25 能被3---9这
七个数字中的哪个数字整除?
平方差公式
导入新课
(a + b)(a - b) = a2 - b2
整式乘法
a2 - b2 = (a + b)(a - b)
因式分解
互逆变形
思考:什么样特征的多项式能用平方差公式分解因式?
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
因式分解
两个数的平方差,等于这两个数的和与这两个数的差的积.
用平方差公式分解因式
★多项式能化成 2 - 2 的形式,就能利用平方差公式进行因式分解.
注意:必须符合
2 - 2 的形式.
√
√
×
×
辨一辨:下列多项式能否用平方差公式来分解因式?为什么?
√
√
(1)x2 + y2
(2)x2 - y2
(3)-x2 - y2
-(x2 + y2)
y2 - x2
(4)-x2 + y2
(5)x2 - 25y2
x2 - (5y)2
(6)9m2 - 1
(3m)2 - 12
例1 分解因式:
解:(1) 原式 =
(2) 原式
典例精析
分解因式:
(1) a2- b2; (2) (a+b)2-4a2
针对训练
=(a+ b)(a- b)
(2) 原式=(a+b)2-(2a)2
=(3a+b)(b-a).
解:(1) 原式=a2-( b)2
=(a+b+2a)(a+b-2a)
例2 分解因式:
解:(1) 原式=( x2 )2 - ( y2 )2
=( x2 + y2 )( x2 - y2)
=(x2 + y2)(x + y)(x - y).
(2) 原式=ab(a2 - 1)
分解因式时,有公因式的一般先提公因式,然后再套用公式分解,最后进行检查
=ab(a + 1)(a - 1).
分解因式:
(1) 5a2m -5b2m; (2) 4y4-4.
针对训练
= 4(y2+1)(y+1)(y-1)
解:(1) 原式 = 5m(a2-b2)
= 5m(a+b)(a-b)
(2) 原式 = 4(y4-1)
= 4(y2+1)(y2-1)
例3 简便计算:
1012 - 992;
解:原式=(101+99)×(101-99)=400.
方法总结:较为复杂的有理数运算,可以运用因式分解对其进行变形,使运算得以简化.
=200×2
=400.
达标检测(每题25分,共100分):
(1) 16a2 - 9b2 = _________________;
(2) (广州中考) xy2 - 9x =_________________;
(3) (徐州中考)16-m4 =___________________;
(4) 53.52×4 - 46.52×4 =____________.
(4a + 3b)(4a - 3b)
x(y + 3)(y - 3)
(4 + m2)(2 + m)(2 - m)
2800
∵ n 为整数,
∴ (2n + 1)2 - 25 能被 4 整除.
已知 n 为整数,(2n + 1)2 - 25 能被 几整除?
解 :原式 = (2n + 1 + 5)(2n + 1 - 5)
= (2n + 6)(2n - 4)
= 2(n + 3)×2(n - 2) = 4(n + 3)(n - 2).
兑奖时刻:你猜对了吗?
书面 作业:
课本119页第2题、4题
谢 谢 聆 听
