人教版八年级数学上册 13.4最短路径问题 教案
文档属性
| 名称 | 人教版八年级数学上册 13.4最短路径问题 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 559.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-23 00:00:00 | ||
图片预览

文档简介
13.4 课题学习 最短路径问题
学习目标:
1.通过探究活动,初步掌握将实际问题抽象为数学问题的方法.
2.通过学习和讨论,学会利用轴对称将最短路径问题转化为 “两点之间,线段最短”问题,体会图形的变化在解决最值问题中的作用,感悟转化思想.
3.能利用所学知识证明所选的路径为最短路径。
重难点:
1.通过探究活动,初步掌握将实际问题抽象为数学问题的方法.
2.通过学习和讨论,学会利用轴对称将最短路径问题转化为 “两点之间,线段最短”问题,体会图形的变化在解决最值问题中的作用,感悟转化思想.
教学过程:
学前准备
(过渡语:最短路径问题一直是我们初中数学的一大难点,不过大家不用害怕,老师在导学案中为大家准备了突破这一难点的装备,大家准备好了吗?)。
1.如图,连接A、B两点的所有连线中,哪条最短?为什么?
②最短,因为两点之间线段最短
2. 如图,你会不会作点A关于直线l的对称点?
3. 如图,点A 和点A ′关于直线l对称,根据轴对称的性质可知,直线l 上任意一点P到点A和点A ′ 的距离PA和P A ′有什么关系?
关于直线l对称的两个点,到直线l上任意一点的距离相等
4. 在我们前面的学习中,涉及比较线段大小的基本事实有哪些?
三角形的三边关系:两边之和大于第三边;
(过渡语:有了这些装备,我们就可以开始我们的探究之旅了。 “将军饮马”是一个实际问题,那么大家能不能把它抽象为一道数学问题呢?)
合作探究
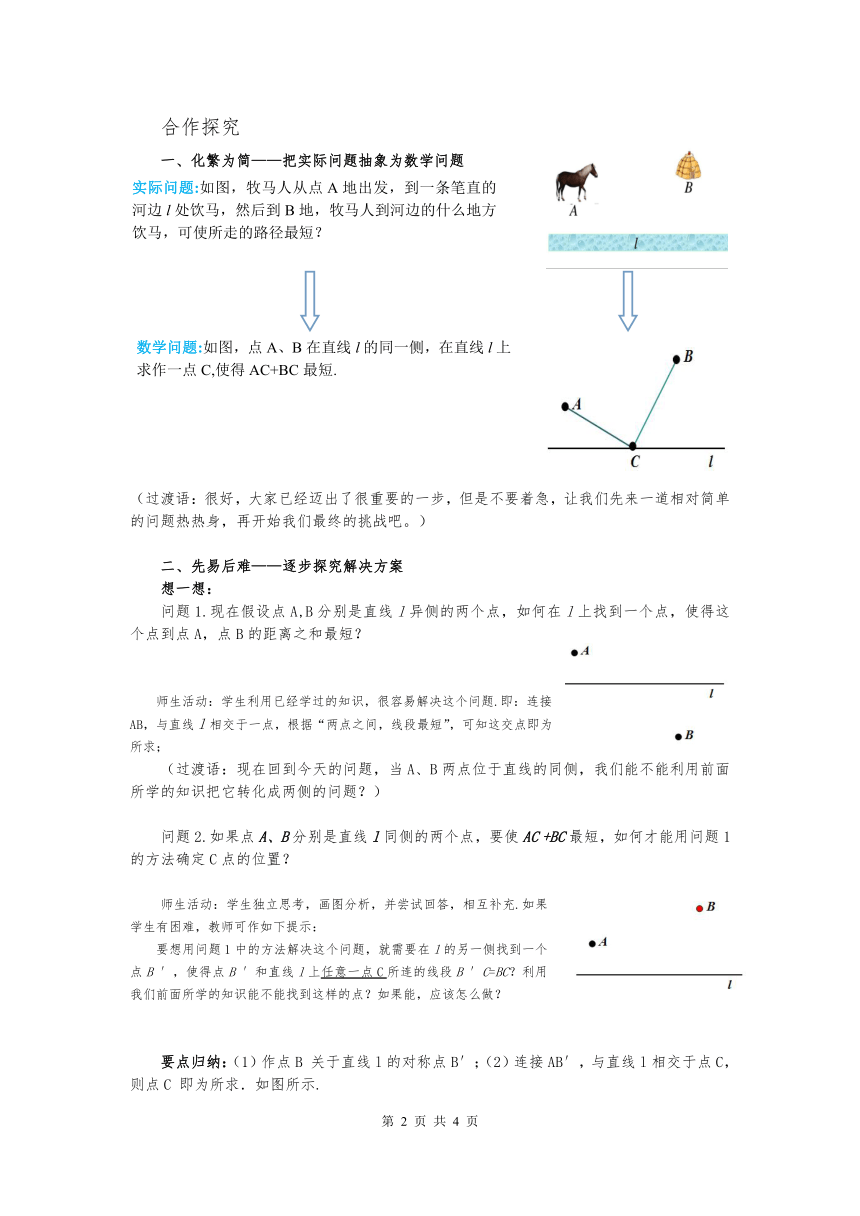
化繁为简——把实际问题抽象为数学问题
(过渡语:很好,大家已经迈出了很重要的一步,但是不要着急,让我们先来一道相对简单的问题热热身,再开始我们最终的挑战吧。)
二、先易后难——逐步探究解决方案
想一想:
问题1.现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点,使得这个点到点A,点B的距离之和最短?
师生活动:学生利用已经学过的知识,很容易解决这个问题.即:连接AB,与直线l相交于一点,根据“两点之间,线段最短”,可知这交点即为所求;
(过渡语:现在回到今天的问题,当A、B两点位于直线的同侧,我们能不能利用前面所学的知识把它转化成两侧的问题?)
问题2.如果点A、B分别是直线l同侧的两个点,要使AC +BC最短,如何才能用问题1的方法确定C点的位置?
师生活动:学生独立思考,画图分析,并尝试回答,相互补充.如果学生有困难,教师可作如下提示:
要想用问题1中的方法解决这个问题,就需要在l的另一侧找到一个点B ′,使得点B ′和直线l上任意一点C所连的线段B ′C=BC?利用我们前面所学的知识能不能找到这样的点?如果能,应该怎么做?
要点归纳:(1)作点B 关于直线l的对称点B′;(2)连接AB′,与直线l相交于点C,则点C 即为所求.如图所示.
(过渡语:太好了,现在我们离成功只有一步之遥了,虽然我们利用轴对称找到了点C,但是它能不能保证AC+BC一定是最短的路径呢?)
三、验证结论——利用数学知识证明探究所得结论
你能不能利用所学的知识证明你所作的点C能使AC +BC最短吗?
师生活动:学生相互交流,教师适时点拨,最后达成共识:若直线l上任意一点(与点C不重合)与A、B两点的距离之和都大于AC+BC,就说明AC+BC最小.
证明:如图,在直线l上任取一点C′(与点C 不重合),连接AC′,BC′,B′C′.由轴对称的性质可知,
BC = B′C,BC′= B′C′.
∴ AC +BC = AC +B′C = AB′,
∴ AC′+BC′= AC′+B′C′.
在△AB′C′中,
AB′<AC′+ B′C′,
∴ AC + BC<AC′+ BC′.
即 AC + BC 最短.
课堂小结
回顾前面的探究活动,我们是通过怎样的过程、借助什么解决问题的?
师生活动:学生回答,并相互补充。(让学生在反思的过程中,体会轴对称的“桥梁”作用,感悟转化思想,丰富数学活动经验.)
当堂训练
如图所示,直线m是△ABC中BC边的垂直平分线,点P是直线m上的动点.若AB=6,AC=4,BC=7,则△APC的周长的最小值是 .
拓展延伸
今天,我们利用轴对称和两点之间线段最短解决了类似将军饮马的最短路径问题,这是我们初中数学当中的一个难点问题,所以需要大家多加练习,课下请大家共同探讨解决导学案上的相关习题。
如图所示,OA、OB是两条公路,在两条公路夹角的内部有一油库P,现在想在两条公路上分别建一个加油站,为使运油的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短,问加油站应如何选址
.如图,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最短,找出E、F两点.
板书设计
课题学习 最短路径问题
1.把实际问题转化为数学问题
2.利用轴对称“化折为直”,依据两点之间线段最短确定最短路径
3.根据两边之和大于第三边进行证明
教学反思
本节课是初中数学的一个难点,为了帮助学生突破这一难点,我在导学案上设计了一些和最短路径问题有关的知识,让学生课前进行了复习。在教学中,首先引导学生把实际问题转化为数学问题,然后从简单的异侧两点的问题入手,逐步引导学生把同侧问题转化为异侧问题,利用轴对称找出最短路径的点。然后利用三角形的三边关系加以证明,验证了此方法的合理性。整节课突出了转化思想在数学学习中的重要性,从学生的反馈来看,整体表现比预计的要好,多数学生通过本节课的学习,完成了学习目标。但是,还需要在以后的习题课上多加练习,最终熟练掌握解决最短路径的方法,并能做到举一反三。
实际问题:如图,牧马人从点A地出发,到一条笔直的河边l处饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?
数学问题:如图,点A、B在直线l的同一侧,在直线l上求作一点C,使得AC+BC最短.
B
O
A
. P
第 4 页 共 4 页
学习目标:
1.通过探究活动,初步掌握将实际问题抽象为数学问题的方法.
2.通过学习和讨论,学会利用轴对称将最短路径问题转化为 “两点之间,线段最短”问题,体会图形的变化在解决最值问题中的作用,感悟转化思想.
3.能利用所学知识证明所选的路径为最短路径。
重难点:
1.通过探究活动,初步掌握将实际问题抽象为数学问题的方法.
2.通过学习和讨论,学会利用轴对称将最短路径问题转化为 “两点之间,线段最短”问题,体会图形的变化在解决最值问题中的作用,感悟转化思想.
教学过程:
学前准备
(过渡语:最短路径问题一直是我们初中数学的一大难点,不过大家不用害怕,老师在导学案中为大家准备了突破这一难点的装备,大家准备好了吗?)。
1.如图,连接A、B两点的所有连线中,哪条最短?为什么?
②最短,因为两点之间线段最短
2. 如图,你会不会作点A关于直线l的对称点?
3. 如图,点A 和点A ′关于直线l对称,根据轴对称的性质可知,直线l 上任意一点P到点A和点A ′ 的距离PA和P A ′有什么关系?
关于直线l对称的两个点,到直线l上任意一点的距离相等
4. 在我们前面的学习中,涉及比较线段大小的基本事实有哪些?
三角形的三边关系:两边之和大于第三边;
(过渡语:有了这些装备,我们就可以开始我们的探究之旅了。 “将军饮马”是一个实际问题,那么大家能不能把它抽象为一道数学问题呢?)
合作探究
化繁为简——把实际问题抽象为数学问题
(过渡语:很好,大家已经迈出了很重要的一步,但是不要着急,让我们先来一道相对简单的问题热热身,再开始我们最终的挑战吧。)
二、先易后难——逐步探究解决方案
想一想:
问题1.现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点,使得这个点到点A,点B的距离之和最短?
师生活动:学生利用已经学过的知识,很容易解决这个问题.即:连接AB,与直线l相交于一点,根据“两点之间,线段最短”,可知这交点即为所求;
(过渡语:现在回到今天的问题,当A、B两点位于直线的同侧,我们能不能利用前面所学的知识把它转化成两侧的问题?)
问题2.如果点A、B分别是直线l同侧的两个点,要使AC +BC最短,如何才能用问题1的方法确定C点的位置?
师生活动:学生独立思考,画图分析,并尝试回答,相互补充.如果学生有困难,教师可作如下提示:
要想用问题1中的方法解决这个问题,就需要在l的另一侧找到一个点B ′,使得点B ′和直线l上任意一点C所连的线段B ′C=BC?利用我们前面所学的知识能不能找到这样的点?如果能,应该怎么做?
要点归纳:(1)作点B 关于直线l的对称点B′;(2)连接AB′,与直线l相交于点C,则点C 即为所求.如图所示.
(过渡语:太好了,现在我们离成功只有一步之遥了,虽然我们利用轴对称找到了点C,但是它能不能保证AC+BC一定是最短的路径呢?)
三、验证结论——利用数学知识证明探究所得结论
你能不能利用所学的知识证明你所作的点C能使AC +BC最短吗?
师生活动:学生相互交流,教师适时点拨,最后达成共识:若直线l上任意一点(与点C不重合)与A、B两点的距离之和都大于AC+BC,就说明AC+BC最小.
证明:如图,在直线l上任取一点C′(与点C 不重合),连接AC′,BC′,B′C′.由轴对称的性质可知,
BC = B′C,BC′= B′C′.
∴ AC +BC = AC +B′C = AB′,
∴ AC′+BC′= AC′+B′C′.
在△AB′C′中,
AB′<AC′+ B′C′,
∴ AC + BC<AC′+ BC′.
即 AC + BC 最短.
课堂小结
回顾前面的探究活动,我们是通过怎样的过程、借助什么解决问题的?
师生活动:学生回答,并相互补充。(让学生在反思的过程中,体会轴对称的“桥梁”作用,感悟转化思想,丰富数学活动经验.)
当堂训练
如图所示,直线m是△ABC中BC边的垂直平分线,点P是直线m上的动点.若AB=6,AC=4,BC=7,则△APC的周长的最小值是 .
拓展延伸
今天,我们利用轴对称和两点之间线段最短解决了类似将军饮马的最短路径问题,这是我们初中数学当中的一个难点问题,所以需要大家多加练习,课下请大家共同探讨解决导学案上的相关习题。
如图所示,OA、OB是两条公路,在两条公路夹角的内部有一油库P,现在想在两条公路上分别建一个加油站,为使运油的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短,问加油站应如何选址
.如图,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最短,找出E、F两点.
板书设计
课题学习 最短路径问题
1.把实际问题转化为数学问题
2.利用轴对称“化折为直”,依据两点之间线段最短确定最短路径
3.根据两边之和大于第三边进行证明
教学反思
本节课是初中数学的一个难点,为了帮助学生突破这一难点,我在导学案上设计了一些和最短路径问题有关的知识,让学生课前进行了复习。在教学中,首先引导学生把实际问题转化为数学问题,然后从简单的异侧两点的问题入手,逐步引导学生把同侧问题转化为异侧问题,利用轴对称找出最短路径的点。然后利用三角形的三边关系加以证明,验证了此方法的合理性。整节课突出了转化思想在数学学习中的重要性,从学生的反馈来看,整体表现比预计的要好,多数学生通过本节课的学习,完成了学习目标。但是,还需要在以后的习题课上多加练习,最终熟练掌握解决最短路径的方法,并能做到举一反三。
实际问题:如图,牧马人从点A地出发,到一条笔直的河边l处饮马,然后到B地,牧马人到河边的什么地方饮马,可使所走的路径最短?
数学问题:如图,点A、B在直线l的同一侧,在直线l上求作一点C,使得AC+BC最短.
B
O
A
. P
第 4 页 共 4 页
