人教版八年级上册第十三章:13.3.2 等边三角形课件
文档属性
| 名称 | 人教版八年级上册第十三章:13.3.2 等边三角形课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-23 00:00:00 | ||
图片预览






文档简介
课件20张PPT。等边三角形学习引入1、什么样的图形叫做等边三角形?等边三角形属于等腰三角形吗?
2、等腰三角形具有什么样的性质?三边都相等的三角形叫做等边三角形。等边三角形是特殊的等腰三角形。 性质1:等腰三角形的两个底角相等(简写“等边对等角”) 性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写“三线合一”)学习目标 1、理解等边三角形的性质和判定方法
2、运用等边三角形的性质和判定方法去解决问题
研读课文 认真阅读课本第79页到第80页的例4.
(一)、完成下面的练习,并体验知识点的形成过程。
1、等边三角形的性质是:
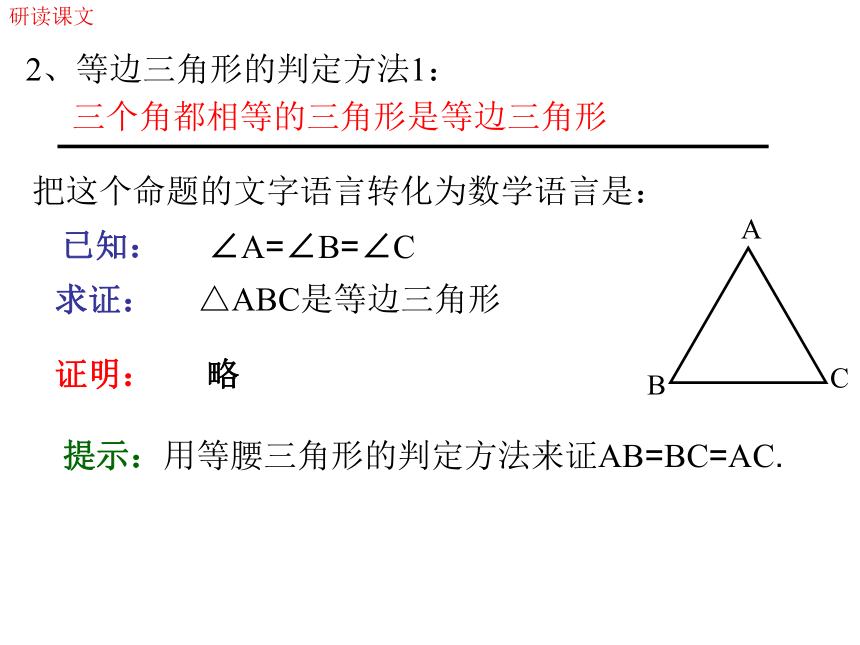
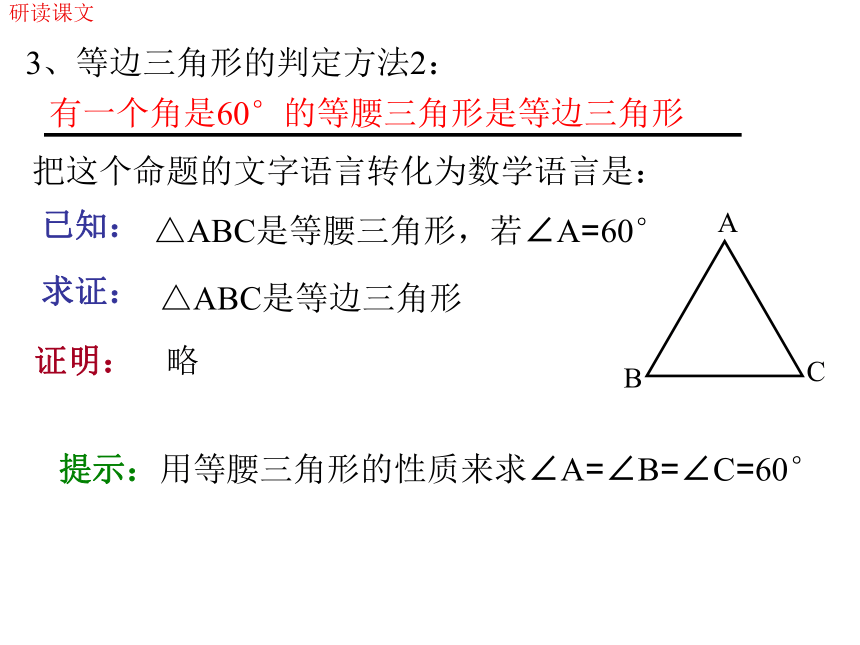
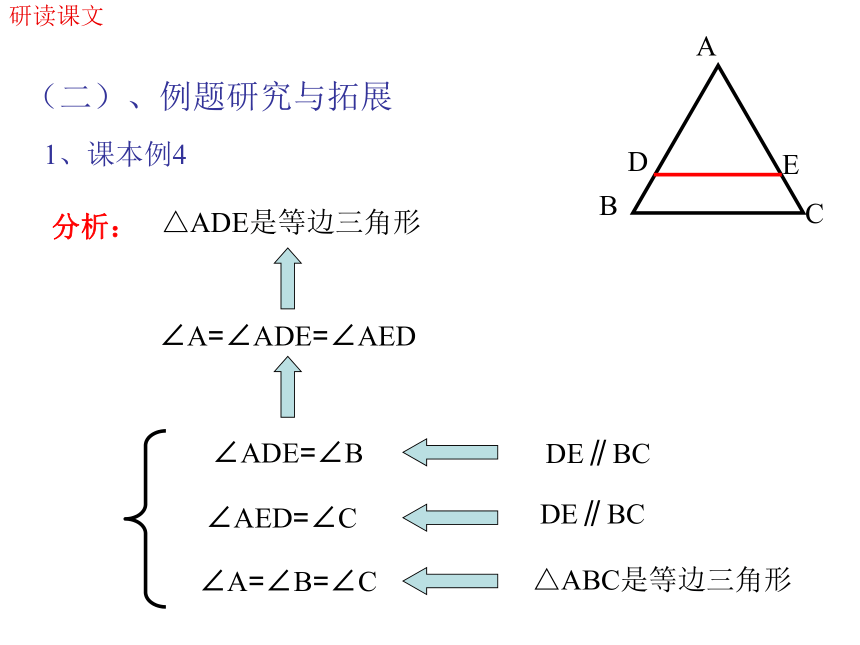
等边三角形的三个内角相等,并且每一个角都等于60°.研读课文等边三角形的三个内角相等,并且每一个角都等于60°把文字语言转化为数学语言:已知:△ABC是等边三角形求证:∠A=∠B=∠C=60°证明: 如果把△ABC看作是AB、AC为腰的等腰三角形,由等腰三角形的性质1,得∠B=∠C如果把△ABC看作是BA、BC为腰的等腰三角形,由 ,得∠A=∠C .∵∠B=∠C且∠A=∠C∴∠A=∠B=∠C … … ( )等腰三角形的性质1等量代换又∵∠A+∠B+∠C =180° …( )三角形内角和定理∴∠A+∠B+∠C =∠A+∠A+∠A=3∠A=180°即:3∠A=180°∴∠A=60°∴∠A=∠B=∠C=60°研读课文2、等边三角形的判定方法1:三个角都相等的三角形是等边三角形把这个命题的文字语言转化为数学语言是: 已知:求证:证明:∠A=∠B=∠C △ABC是等边三角形 略提示:用等腰三角形的判定方法来证AB=BC=AC. 研读课文3、等边三角形的判定方法2: 有一个角是60°的等腰三角形是等边三角形已知:求证:证明:△ABC是等腰三角形,若∠A=60° △ABC是等边三角形 略提示:用等腰三角形的性质来求∠A=∠B=∠C=60° 把这个命题的文字语言转化为数学语言是: 研读课文4、还有其它的等边三角形的判定方法吗?等边三角形的定义: 三边都相等的三角形是等边三角形研读课文(二)、例题研究与拓展 分析: △ADE是等边三角形1、课本例4∠A=∠ADE=∠AED∠ADE=∠B ∠AED=∠C ∠A=∠B=∠C DE∥BC DE∥BC △ABC是等边三角形 研读课文例4 证明证明1:∵ △ABC是等边三角形∴ ∠A=∠B=∠C ……( )等边三角形的性质∵ DE∥BC∴ ∠ADE=∠B,∠AED=∠C …( )两直线平行,同位角相等∴ ∠A=∠ADE=∠AED ……( )等量代换∴ △ADE是等边三角形 ……( )有三个角都相等的三角形是等边三角形研读课文例4 证明证明2:分析: △ADE是等边三角形△ADE是等腰三角形,且∠A=60°AD=AE△ABC是等边三角形∠ADE=∠AEDDE∥BC ∠ADE=∠B DE∥BC ∠AED=∠C 研读课文“例4”的变形题目 如图所示,△ABC是等边三角形,∠BDE与∠DBC互补,
求证:△ADE是等边三角形。提示:∠BDE与∠DBC互补DE∥BC归纳小结 (一)、学生小结:(一)、教师小结:1、这节课我们学到了什么知识?
2、你还有哪些地方是不理解的? 等边三角形是特殊的等腰三角形,具有等腰三角形的所有性质,又具有自己特有的一些性质,要学会在计算和证明中运用这些知识。强化训练【A组训练题】1、如图,等边三角形ABC中,AD是∠BAC的平分线,
则∠BAD = °.
2、如图,△ABC中,AB=AC,∠ACD=120°,则( )
A. △ABC是钝角三角形 B. △ABC是直角三角形
C. △ABC是等边三角形 D. △ABC是不等边三角形
3、如图所示,AB∥CD,∠C=∠D=∠AOB,
则△AOB是 三角形。30C等边强化训练【B组训练题】1、如图,等边三角形ABC中,AD是BC上的高, ∠BDE=∠CDF=60°,求证: BE=CF.AD是BC上的高分析:AD是BC上的中线BD=CD等边△BDE等边△CDFBE=DE = BDCD=DF=CFBE=CF∠B=∠BDE=∠BED=60°∠C=∠CDF=∠CFD=60°BE=CF强化训练【B组训练题】1、如图,等边三角形ABC中,AD是BC上的高, ∠BDE=∠CDF=60°,求证: BE=CF.证明:∵ △ABC是等边三角形∴ ∠B=∠C=60°∵ AD是等边三角形ABC 边BC上的高∴ AD是等边三角形ABC 边BC上的中线∴ BD=CD∵ ∠B=60°, ∠BDE=60°∴ ∠BED=180°- ∠B - ∠BDE=60°∴ ∠B= ∠BDE= ∠BED∴ △BDE是等边三角形 同理:△CDF是等边三角形∵ △BDE和△CDF都是等边三角形,并且 BD=CD∴ BE=DE=BD=CD=DF=CF∴ BE=CF强化训练【B组训练题】2、如图,等边三角形ABC中,AD是∠BAC的平分线, ∠BDE=60°,求证: BE=AE.分析:BE=AEBE=DE=AEBE=BD=DEDE=AE △BDE是等边三角形∠B= ∠BDE=∠BED = 60°△ADE是等腰三角形∠EAD= ∠EDA =30°强化训练【B组训练题】2、如图,等边三角形ABC中,AD是∠BAC的平分线, ∠BDE=60°,求证: BE=AE.证明:∵ △ABC是等边三角形∴ ∠BAC =∠B=∠C=60°∴ ∠BED = 180 °-∠B -∠BDE = 60°∴ ∠B= ∠BDE=∠BED = 60°∴ △BDE是等边三角形∴BE=DE=BD∵ AD是∠BAC的平分线∴ ∠BAD= ∠BAC=30°, AD是等边△ ABC 边BC的高∴ ∠ADB=90°∴ ∠BAD= ∠ADE =30°∴ △ADE是等腰三角形 ∴DE=AE ∴ BE=AE∴ ∠ADE= ∠ADB -∠BDE = 90°- 60°= 30°即:∠EAD= ∠EDA =30°强化训练【C组训练题】1、如图等边三角形ABC中,AD是BC上的高,∠BDE=∠CDF=60°,图中有哪些与BD相等的线段?分析:等边△BDE等边△CDF∠B= ∠BDE=∠BED = 60°∠C=∠CDF=∠CFD=60°BD=CDBD=BE=DE=CD=CF=DFDE=AEDF=AFBD=BE=DE=CD=CF=DF=AE=AF等腰△ADE等腰△ADF∠EAD=∠EDA=30°∠FAD=∠FDA=30°BE=DE = BDCD=DF=CFAD是BC上的中线AD是BC上的高作业布置必做题: P93第11题
选做题: P83第12题
2、等腰三角形具有什么样的性质?三边都相等的三角形叫做等边三角形。等边三角形是特殊的等腰三角形。 性质1:等腰三角形的两个底角相等(简写“等边对等角”) 性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写“三线合一”)学习目标 1、理解等边三角形的性质和判定方法
2、运用等边三角形的性质和判定方法去解决问题
研读课文 认真阅读课本第79页到第80页的例4.
(一)、完成下面的练习,并体验知识点的形成过程。
1、等边三角形的性质是:
等边三角形的三个内角相等,并且每一个角都等于60°.研读课文等边三角形的三个内角相等,并且每一个角都等于60°把文字语言转化为数学语言:已知:△ABC是等边三角形求证:∠A=∠B=∠C=60°证明: 如果把△ABC看作是AB、AC为腰的等腰三角形,由等腰三角形的性质1,得∠B=∠C如果把△ABC看作是BA、BC为腰的等腰三角形,由 ,得∠A=∠C .∵∠B=∠C且∠A=∠C∴∠A=∠B=∠C … … ( )等腰三角形的性质1等量代换又∵∠A+∠B+∠C =180° …( )三角形内角和定理∴∠A+∠B+∠C =∠A+∠A+∠A=3∠A=180°即:3∠A=180°∴∠A=60°∴∠A=∠B=∠C=60°研读课文2、等边三角形的判定方法1:三个角都相等的三角形是等边三角形把这个命题的文字语言转化为数学语言是: 已知:求证:证明:∠A=∠B=∠C △ABC是等边三角形 略提示:用等腰三角形的判定方法来证AB=BC=AC. 研读课文3、等边三角形的判定方法2: 有一个角是60°的等腰三角形是等边三角形已知:求证:证明:△ABC是等腰三角形,若∠A=60° △ABC是等边三角形 略提示:用等腰三角形的性质来求∠A=∠B=∠C=60° 把这个命题的文字语言转化为数学语言是: 研读课文4、还有其它的等边三角形的判定方法吗?等边三角形的定义: 三边都相等的三角形是等边三角形研读课文(二)、例题研究与拓展 分析: △ADE是等边三角形1、课本例4∠A=∠ADE=∠AED∠ADE=∠B ∠AED=∠C ∠A=∠B=∠C DE∥BC DE∥BC △ABC是等边三角形 研读课文例4 证明证明1:∵ △ABC是等边三角形∴ ∠A=∠B=∠C ……( )等边三角形的性质∵ DE∥BC∴ ∠ADE=∠B,∠AED=∠C …( )两直线平行,同位角相等∴ ∠A=∠ADE=∠AED ……( )等量代换∴ △ADE是等边三角形 ……( )有三个角都相等的三角形是等边三角形研读课文例4 证明证明2:分析: △ADE是等边三角形△ADE是等腰三角形,且∠A=60°AD=AE△ABC是等边三角形∠ADE=∠AEDDE∥BC ∠ADE=∠B DE∥BC ∠AED=∠C 研读课文“例4”的变形题目 如图所示,△ABC是等边三角形,∠BDE与∠DBC互补,
求证:△ADE是等边三角形。提示:∠BDE与∠DBC互补DE∥BC归纳小结 (一)、学生小结:(一)、教师小结:1、这节课我们学到了什么知识?
2、你还有哪些地方是不理解的? 等边三角形是特殊的等腰三角形,具有等腰三角形的所有性质,又具有自己特有的一些性质,要学会在计算和证明中运用这些知识。强化训练【A组训练题】1、如图,等边三角形ABC中,AD是∠BAC的平分线,
则∠BAD = °.
2、如图,△ABC中,AB=AC,∠ACD=120°,则( )
A. △ABC是钝角三角形 B. △ABC是直角三角形
C. △ABC是等边三角形 D. △ABC是不等边三角形
3、如图所示,AB∥CD,∠C=∠D=∠AOB,
则△AOB是 三角形。30C等边强化训练【B组训练题】1、如图,等边三角形ABC中,AD是BC上的高, ∠BDE=∠CDF=60°,求证: BE=CF.AD是BC上的高分析:AD是BC上的中线BD=CD等边△BDE等边△CDFBE=DE = BDCD=DF=CFBE=CF∠B=∠BDE=∠BED=60°∠C=∠CDF=∠CFD=60°BE=CF强化训练【B组训练题】1、如图,等边三角形ABC中,AD是BC上的高, ∠BDE=∠CDF=60°,求证: BE=CF.证明:∵ △ABC是等边三角形∴ ∠B=∠C=60°∵ AD是等边三角形ABC 边BC上的高∴ AD是等边三角形ABC 边BC上的中线∴ BD=CD∵ ∠B=60°, ∠BDE=60°∴ ∠BED=180°- ∠B - ∠BDE=60°∴ ∠B= ∠BDE= ∠BED∴ △BDE是等边三角形 同理:△CDF是等边三角形∵ △BDE和△CDF都是等边三角形,并且 BD=CD∴ BE=DE=BD=CD=DF=CF∴ BE=CF强化训练【B组训练题】2、如图,等边三角形ABC中,AD是∠BAC的平分线, ∠BDE=60°,求证: BE=AE.分析:BE=AEBE=DE=AEBE=BD=DEDE=AE △BDE是等边三角形∠B= ∠BDE=∠BED = 60°△ADE是等腰三角形∠EAD= ∠EDA =30°强化训练【B组训练题】2、如图,等边三角形ABC中,AD是∠BAC的平分线, ∠BDE=60°,求证: BE=AE.证明:∵ △ABC是等边三角形∴ ∠BAC =∠B=∠C=60°∴ ∠BED = 180 °-∠B -∠BDE = 60°∴ ∠B= ∠BDE=∠BED = 60°∴ △BDE是等边三角形∴BE=DE=BD∵ AD是∠BAC的平分线∴ ∠BAD= ∠BAC=30°, AD是等边△ ABC 边BC的高∴ ∠ADB=90°∴ ∠BAD= ∠ADE =30°∴ △ADE是等腰三角形 ∴DE=AE ∴ BE=AE∴ ∠ADE= ∠ADB -∠BDE = 90°- 60°= 30°即:∠EAD= ∠EDA =30°强化训练【C组训练题】1、如图等边三角形ABC中,AD是BC上的高,∠BDE=∠CDF=60°,图中有哪些与BD相等的线段?分析:等边△BDE等边△CDF∠B= ∠BDE=∠BED = 60°∠C=∠CDF=∠CFD=60°BD=CDBD=BE=DE=CD=CF=DFDE=AEDF=AFBD=BE=DE=CD=CF=DF=AE=AF等腰△ADE等腰△ADF∠EAD=∠EDA=30°∠FAD=∠FDA=30°BE=DE = BDCD=DF=CFAD是BC上的中线AD是BC上的高作业布置必做题: P93第11题
选做题: P83第12题
