人教版九年级上册第二十二章: 二次函数复习课(15张PPT)
文档属性
| 名称 | 人教版九年级上册第二十二章: 二次函数复习课(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 508.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-23 11:08:01 | ||
图片预览





文档简介
(共15张PPT)
九年级
二次函数复习课
1、了解二次函数的意义;
2、掌握二次函数的图象特征和性质;
3、能解决简单的实际问题.
学习重点: 复习二次函数的重点知识.
学习目标:
1、已知关于x的函数 是二次函数,则m= ______
一、基础知识
-2
(一)二次函数的定义:
一般地,形如 ________ ___________________________
的函数,叫做二次函数.
(a,b,c为常数,a≠0)
(二)二次函数的图象:
名称 表达式 开口方向 对称轴 顶点坐标
一般式
顶点式
(1)二次函数的图像是一条______________;
抛物线
一、基础知识
(2)二次函数的图像:
① 开口方向、对称轴、顶点坐标
a>0,向上
a<0,向下
(二)二次函数的图象:
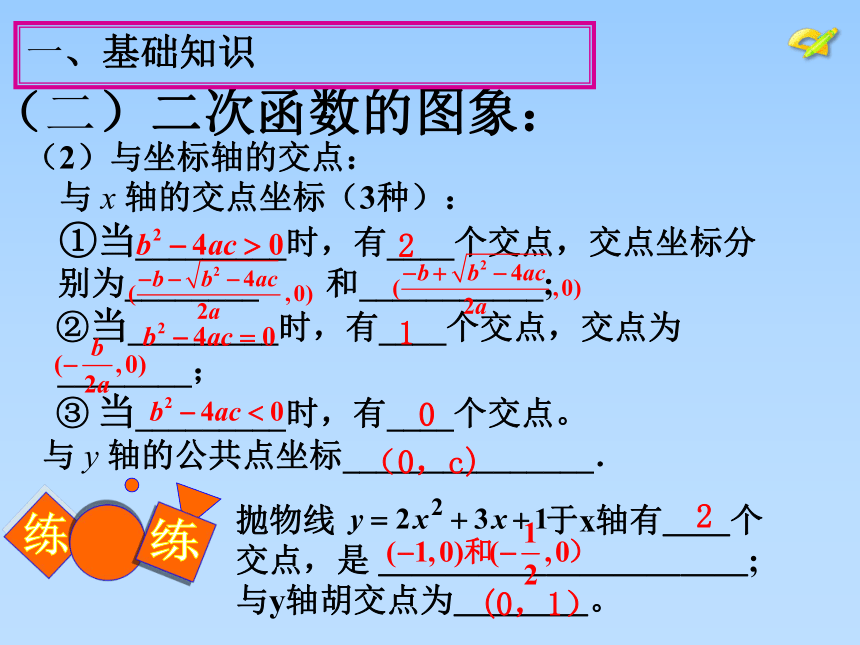
(2)与坐标轴的交点:
与 x 轴的交点坐标(3种):
①当_________时,有____个交点,交点坐标分 别为________ 和___________;
②当_________时,有____个交点,交点为 ________;
③ 当_________时,有____个交点。
与 y 轴的公共点坐标_______________.
一、基础知识
2
1
0
(0,c)
抛物线 于x轴有__个交点,是 ___________;与y轴胡交点为____。
2
(0,1)
(三)二次函数的性质
① 若 a>0,当______,y 随 x 的增大而增大; 当______,y 随 x 的增大而减小;
若 a<0,当______,y 随 x 的增大而增大; 当______,y 随 x 的增大而减小.
② 二次函数的最值
若 a>0,当______时,y 有最____值,是____;
若 a<0,当______时,y 有最____值,是____;
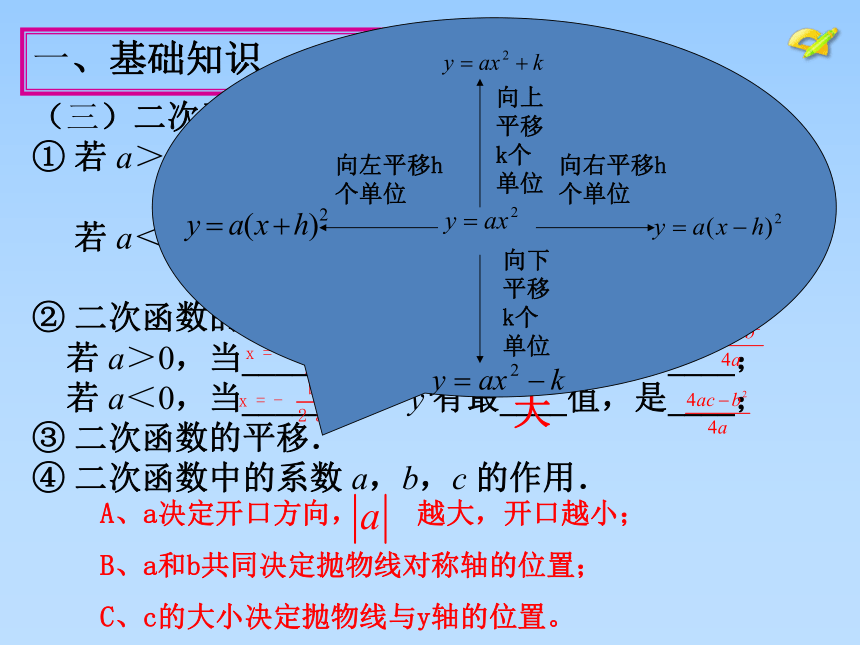
③ 二次函数的平移.
④ 二次函数中的系数 a,b,c 的作用.
一、基础知识
小
大
A、a决定开口方向, 越大,开口越小;
B、a和b共同决定抛物线对称轴的位置;
C、c的大小决定抛物线与y轴的位置。
向右平移h个单位
向上平移 k个单位
向左平移h个单位
向下平移k个单位
2、在抛物线 的开口方向__,对称轴是____,顶点坐标是____,它有最____值,最__值是____,
当 ___时,y随x的增大而增大;
当 ____时,y随x的增大而减小.
1、将抛物线 向右平移1个单位,
再向上平移3个单位,则所得抛物线的表达式为___________________.
向下
(-4,-3)
大
大
-3
一、基础知识
二、强化训练
1.二次函数 的图象如图1所示
当y<0时,自变量x的取值范围是 __ .
(1)
二、强化训练
2.已知二次函数
(1)求出抛物线与坐标轴的交点坐标;
(2)运用配方法化成 的形式;
(3)写出抛物线的开口方向,顶点坐标和对称轴;
(4)当x取何值时,函数y有最值,最值是多少?
(5)它是由抛物线 经过怎样的平移得到的。
二、强化训练
解:(1)在 中,
当x=0时,y= ;
当y=0时,则x=__,
所以抛物线与x轴的交点坐标是 ,
与y轴的交点坐标是 .
-6
3或-1
(0,6)
(3,0),(-1,0 )
(2)
解:(3)抛物线的开口向 ,
顶点坐标为 ,
对称轴为 ______ .
(4)当x= 时,函数y有最 值,最___是 .
(5)它是由抛物线 向__平移__
个单位,再向__平移__个单位得到。
二、强化训练
上
(1,-8)
1
小
-8
小
右
1
下
8
3.某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元.每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
二、强化训练
3.
解:(1)设每件降价x元,每星期利润为y元, 根据题意得:
二、强化训练
当 时 , 。
即:降价2.5元时,每星期的利润最大,最大利润是6125元
三、小结
步骤:
(1).根据实际问题建立二次函数模型;
(2).设自变量建立函数的取值范围;
(3).确定自变量的取值范围;
(4)根据二次函数的图象和性质解二次函数.
(5).根据实际情况得出实际问题的解.
2、二次函数在实际问题中的应用步骤是什么?
根据函数的图像和性质来研究的。
1、我们是如何研究二次函数的?
九年级
二次函数复习课
1、了解二次函数的意义;
2、掌握二次函数的图象特征和性质;
3、能解决简单的实际问题.
学习重点: 复习二次函数的重点知识.
学习目标:
1、已知关于x的函数 是二次函数,则m= ______
一、基础知识
-2
(一)二次函数的定义:
一般地,形如 ________ ___________________________
的函数,叫做二次函数.
(a,b,c为常数,a≠0)
(二)二次函数的图象:
名称 表达式 开口方向 对称轴 顶点坐标
一般式
顶点式
(1)二次函数的图像是一条______________;
抛物线
一、基础知识
(2)二次函数的图像:
① 开口方向、对称轴、顶点坐标
a>0,向上
a<0,向下
(二)二次函数的图象:
(2)与坐标轴的交点:
与 x 轴的交点坐标(3种):
①当_________时,有____个交点,交点坐标分 别为________ 和___________;
②当_________时,有____个交点,交点为 ________;
③ 当_________时,有____个交点。
与 y 轴的公共点坐标_______________.
一、基础知识
2
1
0
(0,c)
抛物线 于x轴有__个交点,是 ___________;与y轴胡交点为____。
2
(0,1)
(三)二次函数的性质
① 若 a>0,当______,y 随 x 的增大而增大; 当______,y 随 x 的增大而减小;
若 a<0,当______,y 随 x 的增大而增大; 当______,y 随 x 的增大而减小.
② 二次函数的最值
若 a>0,当______时,y 有最____值,是____;
若 a<0,当______时,y 有最____值,是____;
③ 二次函数的平移.
④ 二次函数中的系数 a,b,c 的作用.
一、基础知识
小
大
A、a决定开口方向, 越大,开口越小;
B、a和b共同决定抛物线对称轴的位置;
C、c的大小决定抛物线与y轴的位置。
向右平移h个单位
向上平移 k个单位
向左平移h个单位
向下平移k个单位
2、在抛物线 的开口方向__,对称轴是____,顶点坐标是____,它有最____值,最__值是____,
当 ___时,y随x的增大而增大;
当 ____时,y随x的增大而减小.
1、将抛物线 向右平移1个单位,
再向上平移3个单位,则所得抛物线的表达式为___________________.
向下
(-4,-3)
大
大
-3
一、基础知识
二、强化训练
1.二次函数 的图象如图1所示
当y<0时,自变量x的取值范围是 __ .
(1)
二、强化训练
2.已知二次函数
(1)求出抛物线与坐标轴的交点坐标;
(2)运用配方法化成 的形式;
(3)写出抛物线的开口方向,顶点坐标和对称轴;
(4)当x取何值时,函数y有最值,最值是多少?
(5)它是由抛物线 经过怎样的平移得到的。
二、强化训练
解:(1)在 中,
当x=0时,y= ;
当y=0时,则x=__,
所以抛物线与x轴的交点坐标是 ,
与y轴的交点坐标是 .
-6
3或-1
(0,6)
(3,0),(-1,0 )
(2)
解:(3)抛物线的开口向 ,
顶点坐标为 ,
对称轴为 ______ .
(4)当x= 时,函数y有最 值,最___是 .
(5)它是由抛物线 向__平移__
个单位,再向__平移__个单位得到。
二、强化训练
上
(1,-8)
1
小
-8
小
右
1
下
8
3.某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元.每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
二、强化训练
3.
解:(1)设每件降价x元,每星期利润为y元, 根据题意得:
二、强化训练
当 时 , 。
即:降价2.5元时,每星期的利润最大,最大利润是6125元
三、小结
步骤:
(1).根据实际问题建立二次函数模型;
(2).设自变量建立函数的取值范围;
(3).确定自变量的取值范围;
(4)根据二次函数的图象和性质解二次函数.
(5).根据实际情况得出实际问题的解.
2、二次函数在实际问题中的应用步骤是什么?
根据函数的图像和性质来研究的。
1、我们是如何研究二次函数的?
同课章节目录
