人教版九年级下册:28.1 锐角三角函数(1)(21张PPT)
文档属性
| 名称 | 人教版九年级下册:28.1 锐角三角函数(1)(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 294.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-23 11:11:37 | ||
图片预览







文档简介
课件21张PPT。九年级数学(下册)第二十八章 §28.1 锐角三角函数(1)用数学视觉观察世界
用数学思维思考世界主讲人: 怀集县城东中学 武玉燕学习目标1、在直角三角形中,当一个锐角固定时,了解它的对边与斜边的比是固定值
2、理解锐角正弦的概念,掌握正弦的表示方法
3、会根据已知直角三角形的边长求一个锐角的正弦值问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?学.科.网这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB根据“在直角三角形中,30°角所对的边等于斜边的一半”,即可得AB=2BC=70m,也就是说,需要准备70m长的水管. 分析:情
境
探
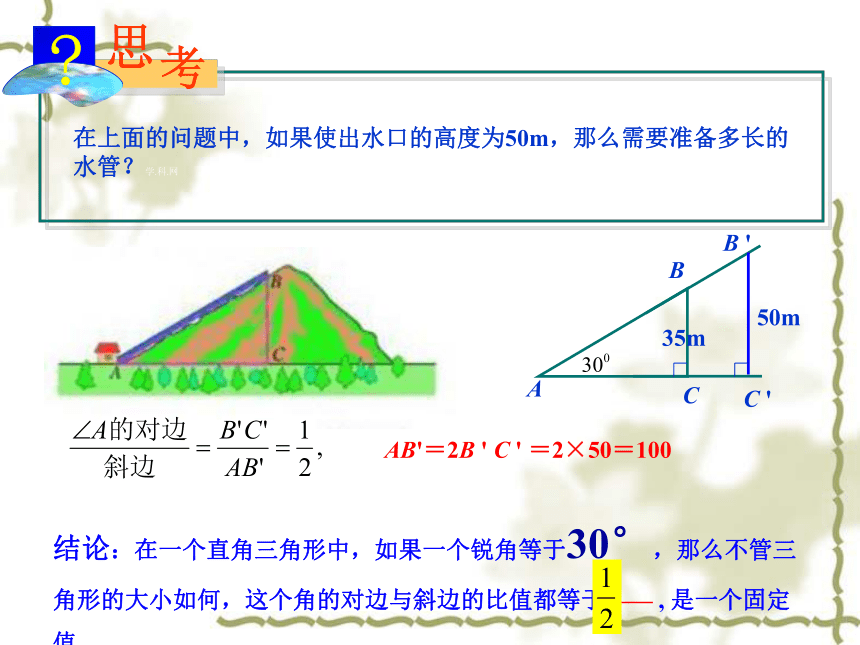
究在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?学.科.网
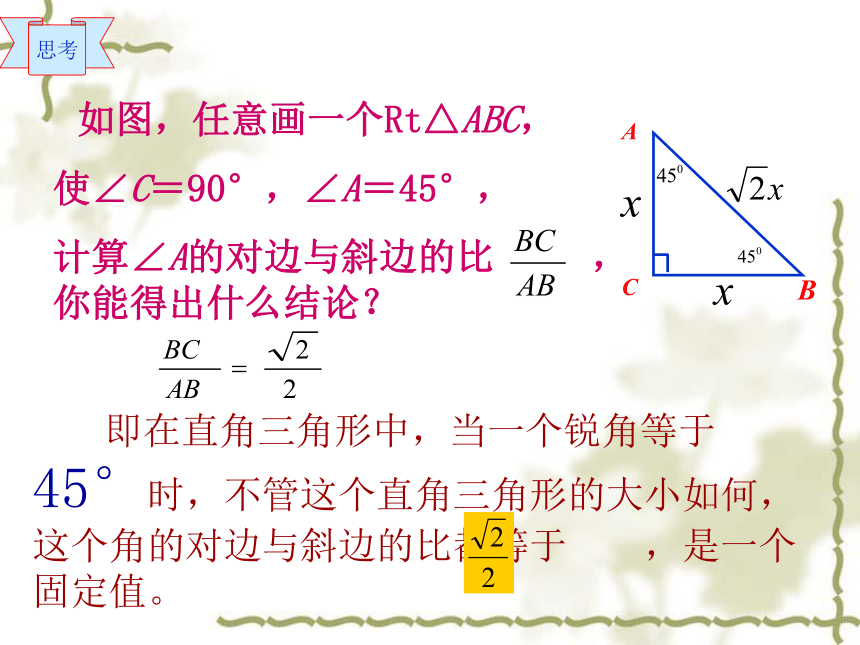
结论:在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于—— , 是一个固定值。ABC50m35mB 'C 'AB'=2B ' C ' =2×50=100 即在直角三角形中,当一个锐角等于45°时,不管这个直角三角形的大小如何,这个角的对边与斜边的比都等于 ,是一个固定值。 如图,任意画一个Rt△ABC,
使∠C=90°,∠A=45°,
计算∠A的对边与斜边的比 ,你能得出什么结论?思考 综上可知,在一个Rt△ABC中,∠C=90°,当一个锐角∠A=30°和∠A=45°时,∠A的对边与斜边的比对应的固定值分别是 和 。 探究 让我们用几何画板来探究一下这个问题那么: 当∠A 取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?当角度改变时,这个固定值会跟着改变吗?由演示得到的结论: 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是一个固定值,这个固定值会随着∠A的改变而改变。
在这个变化过程中,有两个变量 ∠A 和 ∠A的对边与斜边的比, 对于 ∠A 在锐角范围内(0°﹤ ∠A ﹤90°)的每一个确定的值, ∠A的对边与斜边的比 都有唯一确定的值与它对应,因此,∠A的对边与斜边的比是∠A的函数,这种函数有一个名称,叫做正弦函数,简称正弦。 如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA 即例如,当∠A=30°时,我们有当∠A=45°时,我们有 正弦函数的定义例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值. 例 题 示 范求sinA就是要确定∠A的对边与斜边的比;求sinB就是要确定∠B的对边与斜边的比。解:在Rt△ABC中,因为AC=4、BC=3,所以AB=5,
∴SinA=
SinB=
5例2.如图,在Rt △ABC中,∠C=90°,AB=13,BC=5
求sinA和sinB的值.解:在Rt △ABC中,12课堂小结1、在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个_________。
2、在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的____,记作_______。
3、一个相关:正弦值只与角的度数有关。
4、 两种写法: sinA 与 sin∠BAC 。固定值正弦sinA练一练: A组1.判断对错:1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√√××sinA是一个比值,单位已约去,结果不再有单位;2)如图,sinA= ( ) ×2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定C练一练练一练 B组
根据右图,求sinA和sinB的值
提示:由勾股定理求得
AB=
∴SinA=
SinB=ACB35 分别求出图中∠A, ∠B的正弦值
ABC26BCA1.正弦函数的定义:2.sinA是∠A的正弦函数. Sin300 =sin45°=对于∠A的每一个值(0°<A<90°),sinA都有唯一确定的值与之对应。在平面直角平面坐标系中,已知点A(3,0)和B(0,-4),则sin∠OAB等于____345 求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。 如图, ∠C=90°,CD⊥AB。sinB可以由哪两条线段之比求得?想一想若AC=5,CD=3,求sinB的值.解: ∵∠B=∠ACD ∴ sinB=sin∠ACD在Rt△ACD中,AD=sin ∠ACD=∴ sinB==4354课外题求下列各式的值:
(1)Sin45°+Sin30°=
(2)Sin45°+ =
(3)Sin45°- =
(4)1-2Sin30°=同学们,再见!
用数学思维思考世界主讲人: 怀集县城东中学 武玉燕学习目标1、在直角三角形中,当一个锐角固定时,了解它的对边与斜边的比是固定值
2、理解锐角正弦的概念,掌握正弦的表示方法
3、会根据已知直角三角形的边长求一个锐角的正弦值问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?学.科.网这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB根据“在直角三角形中,30°角所对的边等于斜边的一半”,即可得AB=2BC=70m,也就是说,需要准备70m长的水管. 分析:情
境
探
究在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?学.科.网
结论:在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于—— , 是一个固定值。ABC50m35mB 'C 'AB'=2B ' C ' =2×50=100 即在直角三角形中,当一个锐角等于45°时,不管这个直角三角形的大小如何,这个角的对边与斜边的比都等于 ,是一个固定值。 如图,任意画一个Rt△ABC,
使∠C=90°,∠A=45°,
计算∠A的对边与斜边的比 ,你能得出什么结论?思考 综上可知,在一个Rt△ABC中,∠C=90°,当一个锐角∠A=30°和∠A=45°时,∠A的对边与斜边的比对应的固定值分别是 和 。 探究 让我们用几何画板来探究一下这个问题那么: 当∠A 取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?当角度改变时,这个固定值会跟着改变吗?由演示得到的结论: 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是一个固定值,这个固定值会随着∠A的改变而改变。
在这个变化过程中,有两个变量 ∠A 和 ∠A的对边与斜边的比, 对于 ∠A 在锐角范围内(0°﹤ ∠A ﹤90°)的每一个确定的值, ∠A的对边与斜边的比 都有唯一确定的值与它对应,因此,∠A的对边与斜边的比是∠A的函数,这种函数有一个名称,叫做正弦函数,简称正弦。 如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA 即例如,当∠A=30°时,我们有当∠A=45°时,我们有 正弦函数的定义例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值. 例 题 示 范求sinA就是要确定∠A的对边与斜边的比;求sinB就是要确定∠B的对边与斜边的比。解:在Rt△ABC中,因为AC=4、BC=3,所以AB=5,
∴SinA=
SinB=
5例2.如图,在Rt △ABC中,∠C=90°,AB=13,BC=5
求sinA和sinB的值.解:在Rt △ABC中,12课堂小结1、在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个_________。
2、在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的____,记作_______。
3、一个相关:正弦值只与角的度数有关。
4、 两种写法: sinA 与 sin∠BAC 。固定值正弦sinA练一练: A组1.判断对错:1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√√××sinA是一个比值,单位已约去,结果不再有单位;2)如图,sinA= ( ) ×2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定C练一练练一练 B组
根据右图,求sinA和sinB的值
提示:由勾股定理求得
AB=
∴SinA=
SinB=ACB35 分别求出图中∠A, ∠B的正弦值
ABC26BCA1.正弦函数的定义:2.sinA是∠A的正弦函数. Sin300 =sin45°=对于∠A的每一个值(0°<A<90°),sinA都有唯一确定的值与之对应。在平面直角平面坐标系中,已知点A(3,0)和B(0,-4),则sin∠OAB等于____345 求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。 如图, ∠C=90°,CD⊥AB。sinB可以由哪两条线段之比求得?想一想若AC=5,CD=3,求sinB的值.解: ∵∠B=∠ACD ∴ sinB=sin∠ACD在Rt△ACD中,AD=sin ∠ACD=∴ sinB==4354课外题求下列各式的值:
(1)Sin45°+Sin30°=
(2)Sin45°+ =
(3)Sin45°- =
(4)1-2Sin30°=同学们,再见!
