人教版九年级下册:28.1锐角三角函数- 正弦课件
文档属性
| 名称 | 人教版九年级下册:28.1锐角三角函数- 正弦课件 |  | |
| 格式 | zip | ||
| 文件大小 | 492.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-23 11:12:21 | ||
图片预览



文档简介
课件17张PPT。新人教版九年级数学(下册)第二十八章 28.1 正 弦用数学视觉观察世界
用数学思维思考世界梁 村 中 学
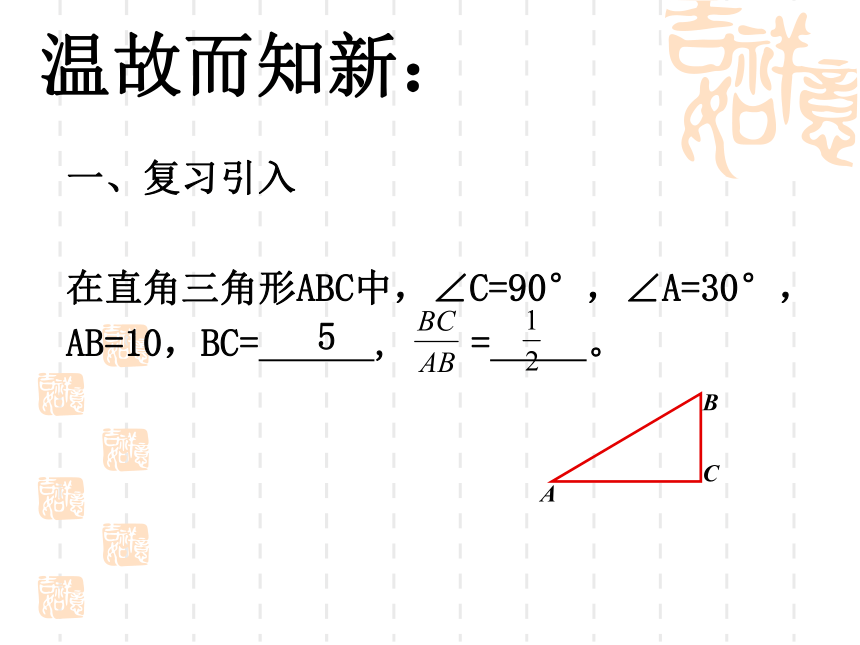
授课人:罗学鹏一、复习引入
在直角三角形ABC中,∠C=90°,∠A=30°,
AB=10,BC= , = 。
温故而知新:5学习目标
1、理解锐角的正弦的概念及其表示方法。
2、会用锐角的正弦解决问题。
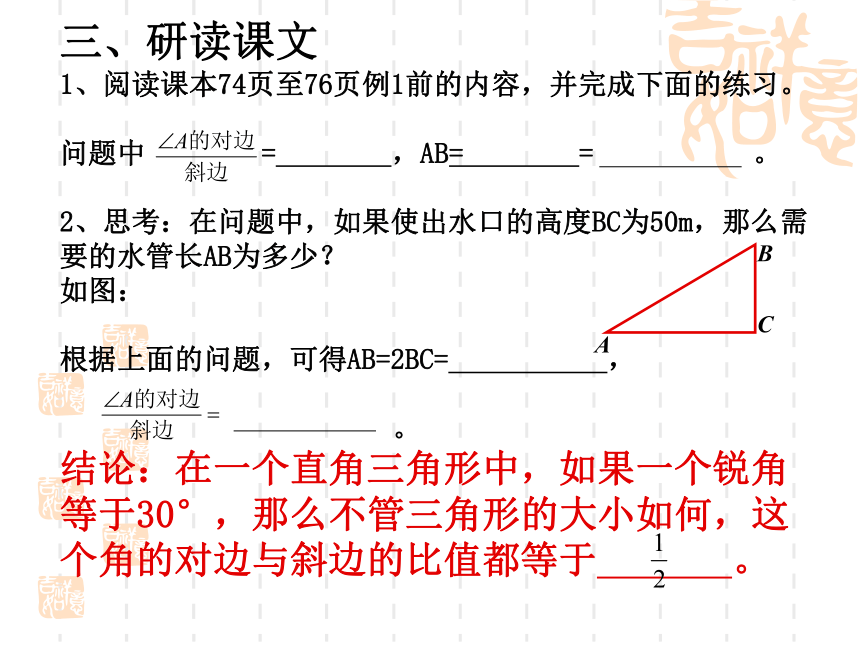
三、研读课文
1、阅读课本74页至76页例1前的内容,并完成下面的练习。
问题中 = ,AB= = 。
2、思考:在问题中,如果使出水口的高度BC为50m,那么需要的水管长AB为多少?
如图:
根据上面的问题,可得AB=2BC= ,
。
结论:在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 。
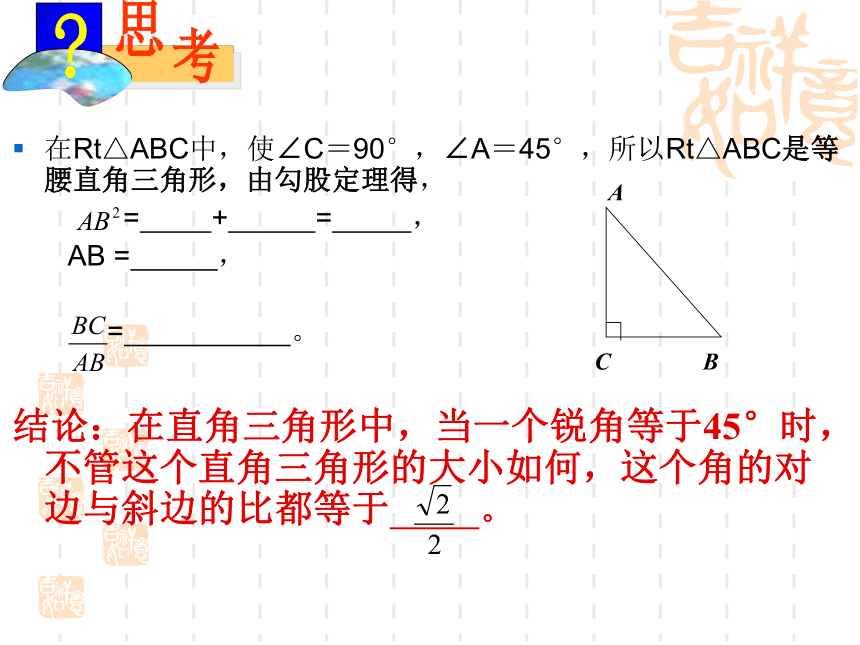
在Rt△ABC中,使∠C=90°,∠A=45°,所以Rt△ABC是等腰直角三角形,由勾股定理得,
= + = ,
AB = ,
= 。
结论:在直角三角形中,当一个锐角等于45°时,不管这个直角三角形的大小如何,这个角的对边与斜边的比都等于 。 ABC
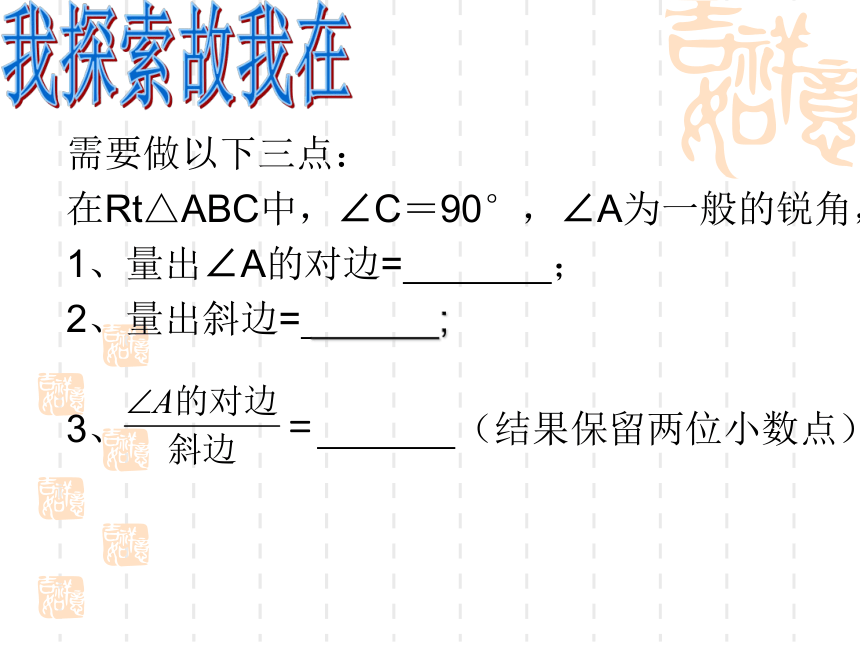
当∠A为一般的锐角时,那么它的对边与
斜边的比是否也是一个固定的值?
需要做以下三点:
在Rt△ABC中,∠C=90°,∠A为一般的锐角,
1、量出∠A的对边= ;
2、量出斜边= ;
3、 (结果保留两位小数点)
=我探索故我在在直角三角形中,当锐角A的度数 时,不管三角形的大小如何,∠A的对边与斜边的比都是一个 值。一定固定结 论 在Rt△ABC中,∠C=90°,我们把锐角A的
对边与斜边的比值叫做∠A的正弦(sine),
记作sinA 即 揭示定义b对边a斜边c注意:
“sinA”是一个完整的符号,不要误解成“sin×A”,单独写符号sin是没有意义的,记号里习惯省去角的符号“∠” 。
正弦的表示:sinA 、 sin39 ° 、 sin β(省去角的符号)
sin∠DEF、 sin∠1 (不能省去角的符号)例1 :如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.解: (1)在Rt△ABC中, 例 题 示 范 课堂小结 你今天学到了什么知识?感受到了什么?你对正弦的定义还存在什么疑惑吗?A组练习1.判断对错:1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
sinA是一个比值(注意比的顺序),无单位;2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定
3.在Rt△ABC中,∠C=90°,若AB=5,AC=4,则sinA=( )
A. B. C. D.练一练CB
1、在Rt△ABC中,sinA= ,AB=10,则BC=______
2、如下图:在Rt△ABC中, ∠C=90°, AD是BC边上的中线,AC=2,BC=4,
sin∠DAC=_____.
B组练习ACBD┌8C组练习
如图,在△ABC 中,∠ACB=90°,BC=3,AC=4,CD⊥AB,垂足为D,求sin∠ACD解:∵∠ACB=90°,BC=3,AC=4
∴在Rt△ABC中,
5AB=∵S= AC?BC= AB?CD
∴×4×3= ×5CD, 即CD=∵CD⊥AB
∴在Rt△ABC中,AD=∴sin∠ACD=÷4=作业:课本82页习题28.1 第1题(只做与正弦函数有关的部分)
用数学思维思考世界梁 村 中 学
授课人:罗学鹏一、复习引入
在直角三角形ABC中,∠C=90°,∠A=30°,
AB=10,BC= , = 。
温故而知新:5学习目标
1、理解锐角的正弦的概念及其表示方法。
2、会用锐角的正弦解决问题。
三、研读课文
1、阅读课本74页至76页例1前的内容,并完成下面的练习。
问题中 = ,AB= = 。
2、思考:在问题中,如果使出水口的高度BC为50m,那么需要的水管长AB为多少?
如图:
根据上面的问题,可得AB=2BC= ,
。
结论:在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 。
在Rt△ABC中,使∠C=90°,∠A=45°,所以Rt△ABC是等腰直角三角形,由勾股定理得,
= + = ,
AB = ,
= 。
结论:在直角三角形中,当一个锐角等于45°时,不管这个直角三角形的大小如何,这个角的对边与斜边的比都等于 。 ABC
当∠A为一般的锐角时,那么它的对边与
斜边的比是否也是一个固定的值?
需要做以下三点:
在Rt△ABC中,∠C=90°,∠A为一般的锐角,
1、量出∠A的对边= ;
2、量出斜边= ;
3、 (结果保留两位小数点)
=我探索故我在在直角三角形中,当锐角A的度数 时,不管三角形的大小如何,∠A的对边与斜边的比都是一个 值。一定固定结 论 在Rt△ABC中,∠C=90°,我们把锐角A的
对边与斜边的比值叫做∠A的正弦(sine),
记作sinA 即 揭示定义b对边a斜边c注意:
“sinA”是一个完整的符号,不要误解成“sin×A”,单独写符号sin是没有意义的,记号里习惯省去角的符号“∠” 。
正弦的表示:sinA 、 sin39 ° 、 sin β(省去角的符号)
sin∠DEF、 sin∠1 (不能省去角的符号)例1 :如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.解: (1)在Rt△ABC中, 例 题 示 范 课堂小结 你今天学到了什么知识?感受到了什么?你对正弦的定义还存在什么疑惑吗?A组练习1.判断对错:1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
sinA是一个比值(注意比的顺序),无单位;2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定
3.在Rt△ABC中,∠C=90°,若AB=5,AC=4,则sinA=( )
A. B. C. D.练一练CB
1、在Rt△ABC中,sinA= ,AB=10,则BC=______
2、如下图:在Rt△ABC中, ∠C=90°, AD是BC边上的中线,AC=2,BC=4,
sin∠DAC=_____.
B组练习ACBD┌8C组练习
如图,在△ABC 中,∠ACB=90°,BC=3,AC=4,CD⊥AB,垂足为D,求sin∠ACD解:∵∠ACB=90°,BC=3,AC=4
∴在Rt△ABC中,
5AB=∵S= AC?BC= AB?CD
∴×4×3= ×5CD, 即CD=∵CD⊥AB
∴在Rt△ABC中,AD=∴sin∠ACD=÷4=作业:课本82页习题28.1 第1题(只做与正弦函数有关的部分)
