1.4.2 充要条件 作业(含解析) 高中数学(人教A版2019)必修第一册
文档属性
| 名称 | 1.4.2 充要条件 作业(含解析) 高中数学(人教A版2019)必修第一册 |  | |
| 格式 | docx | ||
| 文件大小 | 79.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-23 10:59:46 | ||
图片预览

文档简介
1.4.2 充要条件 作业
【基础训练】
1.“x>0”是“x≠0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.(河南洛阳高一期中)设A,B是两个集合,则“A B”是“A∪B=B”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.设p:四边形为菱形,q:四边形的对角线互相垂直,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.(河北保定高一月考)设a,b∈R,则“ab+1=a+b”的充要条件是( )
A.a,b都为1 B.a,b都不为1
C.a,b中至少有一个为1 D.a,b都不为0
5.“方程x2-2x-a=0没有实数根”的充要条件是________.
6.从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一个合适的填空.
(1)“x2-1=0”是“|x|-1=0”的________;
(2)“x<5”是“x<3”的________________.
7.求证:一次函数y=kx+b(k≠0)的图象过原点的充要条件是b=0.
【能力训练】
8.(多选)下列结论中正确的是( )
A.“x2>4”是“x<-2”的必要不充分条件
B.在△ABC中,“AB2+AC2=BC2”是“△ABC为直角三角形”的充要条件
C.若a,b∈R,则“a2+b2≠0”是“a,b不全为0”的充要条件
D.“x为无理数”是“x2为无理数”的必要不充分条件
9.使不等式0<<1成立的一个充分不必要条件是( )
A.0<x< B.x>1
C.x>2 D.x<0
10在人类中,双眼皮由显性基因A控制,单眼皮由隐性基因a控制,当一个人的基因型为AA或 Aa时,这个人就是双眼皮,当一个人的基因型为aa 时,这个人就是单眼皮.随机从父母的基因中各选出一个 A或者a基因遗传给孩子组合成新的基因.根据以上信息,则“父母均为单眼皮”是“孩子为单眼皮”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
11.函数y=x2+mx+1的图象关于直线x=1对称的充要条件是m=________.
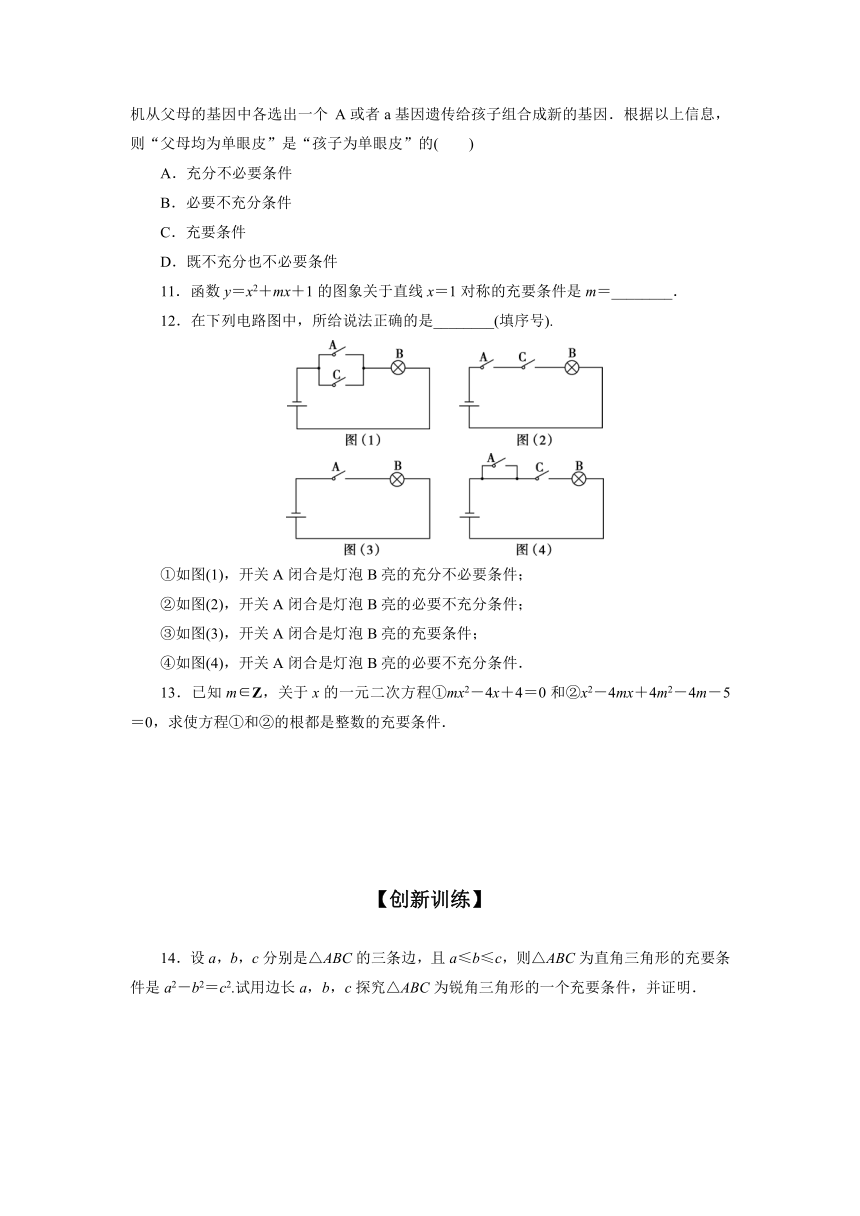
12.在下列电路图中,所给说法正确的是________(填序号).
①如图(1),开关A闭合是灯泡B亮的充分不必要条件;
②如图(2),开关A闭合是灯泡B亮的必要不充分条件;
③如图(3),开关A闭合是灯泡B亮的充要条件;
④如图(4),开关A闭合是灯泡B亮的必要不充分条件.
13.已知m∈Z,关于x的一元二次方程①mx2-4x+4=0和②x2-4mx+4m2-4m-5=0,求使方程①和②的根都是整数的充要条件.
【创新训练】
14.设a,b,c分别是△ABC的三条边,且a≤b≤c,则△ABC为直角三角形的充要条件是a2-b2=c2.试用边长a,b,c探究△ABC为锐角三角形的一个充要条件,并证明.
答案解析
1.答案 A
解析 由“x>0” “x≠0”,反之不一定成立.因此“x>0”是“x≠0”的充分不必要条件.
2.答案 C
解析 由A∪B=B,得A B,反之亦成立,则“A B”是“A∪B=B”的充要条件.故选C.
3.答案 A
解析 若四边形为菱形,则该四边形的对角线互相垂直,即p q;反之,四边形的对角线互相垂直时,该四边形不一定是菱形,即qp.所以p是q的充分不必要条件.
4.答案 C
解析 因为ab+1=a+b,所以a(b-1)-(b-1)=0,所以(b-1)(a-1)=0,解得a=1或b=1,所以a,b中至少有一个为1. 故选C.
5.答案 a<-1
解析 因为方程x2-2x-a=0没有实数根,所以有Δ=4+4a<0,解得a<-1,因此“方程x2-2x-a=0没有实数根”的必要条件是a<-1.反之,若a<-1,则Δ<0,方程x2-2x-a=0无实数根,从而充分性成立.故“方程x2-2x-a=0没有实数根”的充要条件是“a<-1”.
6.答案 (1)充要条件 (2)必要不充分条件
解析 (1)x2-1=0 |x|-1=0,
∴“x2-1=0”是“|x|-1=0”的充要条件;
(2)x<3 x<5,但x<5x<3,∴“x<5”是“x<3”的必要不充分条件.
7.证明 ①充分性:如果b=0,那么y=kx,
当x=0时,y=0,函数图象过原点.
②必要性:因为y=kx+b(k≠0)的图象过原点,
所以当x=0时,y=0,即0=k·0+b,所以b=0.
综上,一次函数y=kx+b(k≠0)的图象过原点的充要条件是b=0.
8.答案 ACD
解析 x<-2 x2>4,但x2>4 x>2或x<-2,故A正确;AB2+AC2=BC2 △ABC为直角三角形,反之,若△ABC为直角三角形,当B,C为直角时,不能推出AB2+AC2=BC2,故B错误;a2+b2≠0 a,b不全为0,反之,由a,b不全为0 a2+b2≠0,故C正确;当x2为无理数时,x为无理数,反之不成立,故D正确.故选ACD.
9.答案 C
解析 0<<1 x>1,故使不等式0<<1成立的一个充分不必要条件可以是x>2.
10.答案 A
解析 若“父母均为单眼皮”,即父母的基因型都是aa,所以孩子的基因型也一定是aa,所以一定有“孩子为单眼皮”.
若“孩子为单眼皮”,则孩子的基因型是aa,但是父母的基因型可能都是Aa或一个是Aa,一个是aa,所以父母中有可能有双眼皮,所以“父母均为单眼皮”是“孩子为单眼皮”的充分不必要条件.故选A.
11.答案 -2
解析 当m=-2时,y=x2-2x+1,其图象关于直线x=1对称,反之也成立,所以函数y=x2+mx+1的图象关于直线x=1对称的充要条件是m=-2.
12.答案 ①②③
解析 对于①,开关A闭合,灯泡B亮;而灯泡B亮时,开关A不一定闭合,所以开关A闭合是灯泡B亮的充分不必要条件,①正确.对于②,开关A闭合,灯泡B不一定亮;而灯泡B亮时,开关A必须闭合,所以开关A闭合是灯泡B亮的必要不充分条件,②正确.对于③,开关A闭合,灯泡B亮;而灯泡B亮时,开关A必须闭合,所以开关A闭合是灯泡B亮的充要条件,③正确.对于④,开关A闭合,灯泡B不一定亮;而灯泡B亮时,开关A不一定闭合,所以开关A闭合是灯泡B亮的既不充分也不必要条件,④错误.
13.解 由已知条件得m≠0.
方程①有实数根的充要条件是Δ=16-4m×4≥0且m≠0,解得m≤1且m≠0.
方程②有实数根的充要条件是Δ=16m2-4(4m2-4m-5)≥0,解得m≥-.所以-≤m≤1且m≠0.
因为m∈Z,所以m=-1或m=1.
当m=-1时,方程①为x2+4x-4=0,无整数根;
当m=1时,方程①为x2-4x+4=0,
方程②为x2-4x-5=0,均有整数根.
所以,方程①和②的根都是整数 m=1;反之,m=1 方程①和②的根都是整数.
故方程①和②的根都是整数的充要条件为m=1.
14.解 △ABC为锐角三角形的充要条件为a2+b2>c2.
证明:充分性:若a2+b2>c2,则△ABC不是直角三角形.
若△ABC为钝角三角形,则∠C>90°,
过点B作AC的延长线的垂线,垂足为D(如图(1)),
由勾股定理知c2=BD2+(b+CD)2=BD2+CD2+b2+2·CD·b=a2+b2+2·CD·b>a2+b2,矛盾,
故△ABC为锐角三角形,充分性成立.
必要性:过点A作边BC的垂线,垂足为D(如图(2)),
由勾股定理知,c2=AD2+BD2=AD2+(a-CD)2=b2-CD2+(a-CD)2=a2+b2-2·CD·a<a2+b2.故必要性成立.
故△ABC为锐角三角形的充要条件为a2+b2>c2.
【基础训练】
1.“x>0”是“x≠0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.(河南洛阳高一期中)设A,B是两个集合,则“A B”是“A∪B=B”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.设p:四边形为菱形,q:四边形的对角线互相垂直,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.(河北保定高一月考)设a,b∈R,则“ab+1=a+b”的充要条件是( )
A.a,b都为1 B.a,b都不为1
C.a,b中至少有一个为1 D.a,b都不为0
5.“方程x2-2x-a=0没有实数根”的充要条件是________.
6.从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一个合适的填空.
(1)“x2-1=0”是“|x|-1=0”的________;
(2)“x<5”是“x<3”的________________.
7.求证:一次函数y=kx+b(k≠0)的图象过原点的充要条件是b=0.
【能力训练】
8.(多选)下列结论中正确的是( )
A.“x2>4”是“x<-2”的必要不充分条件
B.在△ABC中,“AB2+AC2=BC2”是“△ABC为直角三角形”的充要条件
C.若a,b∈R,则“a2+b2≠0”是“a,b不全为0”的充要条件
D.“x为无理数”是“x2为无理数”的必要不充分条件
9.使不等式0<<1成立的一个充分不必要条件是( )
A.0<x< B.x>1
C.x>2 D.x<0
10在人类中,双眼皮由显性基因A控制,单眼皮由隐性基因a控制,当一个人的基因型为AA或 Aa时,这个人就是双眼皮,当一个人的基因型为aa 时,这个人就是单眼皮.随机从父母的基因中各选出一个 A或者a基因遗传给孩子组合成新的基因.根据以上信息,则“父母均为单眼皮”是“孩子为单眼皮”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
11.函数y=x2+mx+1的图象关于直线x=1对称的充要条件是m=________.
12.在下列电路图中,所给说法正确的是________(填序号).
①如图(1),开关A闭合是灯泡B亮的充分不必要条件;
②如图(2),开关A闭合是灯泡B亮的必要不充分条件;
③如图(3),开关A闭合是灯泡B亮的充要条件;
④如图(4),开关A闭合是灯泡B亮的必要不充分条件.
13.已知m∈Z,关于x的一元二次方程①mx2-4x+4=0和②x2-4mx+4m2-4m-5=0,求使方程①和②的根都是整数的充要条件.
【创新训练】
14.设a,b,c分别是△ABC的三条边,且a≤b≤c,则△ABC为直角三角形的充要条件是a2-b2=c2.试用边长a,b,c探究△ABC为锐角三角形的一个充要条件,并证明.
答案解析
1.答案 A
解析 由“x>0” “x≠0”,反之不一定成立.因此“x>0”是“x≠0”的充分不必要条件.
2.答案 C
解析 由A∪B=B,得A B,反之亦成立,则“A B”是“A∪B=B”的充要条件.故选C.
3.答案 A
解析 若四边形为菱形,则该四边形的对角线互相垂直,即p q;反之,四边形的对角线互相垂直时,该四边形不一定是菱形,即qp.所以p是q的充分不必要条件.
4.答案 C
解析 因为ab+1=a+b,所以a(b-1)-(b-1)=0,所以(b-1)(a-1)=0,解得a=1或b=1,所以a,b中至少有一个为1. 故选C.
5.答案 a<-1
解析 因为方程x2-2x-a=0没有实数根,所以有Δ=4+4a<0,解得a<-1,因此“方程x2-2x-a=0没有实数根”的必要条件是a<-1.反之,若a<-1,则Δ<0,方程x2-2x-a=0无实数根,从而充分性成立.故“方程x2-2x-a=0没有实数根”的充要条件是“a<-1”.
6.答案 (1)充要条件 (2)必要不充分条件
解析 (1)x2-1=0 |x|-1=0,
∴“x2-1=0”是“|x|-1=0”的充要条件;
(2)x<3 x<5,但x<5x<3,∴“x<5”是“x<3”的必要不充分条件.
7.证明 ①充分性:如果b=0,那么y=kx,
当x=0时,y=0,函数图象过原点.
②必要性:因为y=kx+b(k≠0)的图象过原点,
所以当x=0时,y=0,即0=k·0+b,所以b=0.
综上,一次函数y=kx+b(k≠0)的图象过原点的充要条件是b=0.
8.答案 ACD
解析 x<-2 x2>4,但x2>4 x>2或x<-2,故A正确;AB2+AC2=BC2 △ABC为直角三角形,反之,若△ABC为直角三角形,当B,C为直角时,不能推出AB2+AC2=BC2,故B错误;a2+b2≠0 a,b不全为0,反之,由a,b不全为0 a2+b2≠0,故C正确;当x2为无理数时,x为无理数,反之不成立,故D正确.故选ACD.
9.答案 C
解析 0<<1 x>1,故使不等式0<<1成立的一个充分不必要条件可以是x>2.
10.答案 A
解析 若“父母均为单眼皮”,即父母的基因型都是aa,所以孩子的基因型也一定是aa,所以一定有“孩子为单眼皮”.
若“孩子为单眼皮”,则孩子的基因型是aa,但是父母的基因型可能都是Aa或一个是Aa,一个是aa,所以父母中有可能有双眼皮,所以“父母均为单眼皮”是“孩子为单眼皮”的充分不必要条件.故选A.
11.答案 -2
解析 当m=-2时,y=x2-2x+1,其图象关于直线x=1对称,反之也成立,所以函数y=x2+mx+1的图象关于直线x=1对称的充要条件是m=-2.
12.答案 ①②③
解析 对于①,开关A闭合,灯泡B亮;而灯泡B亮时,开关A不一定闭合,所以开关A闭合是灯泡B亮的充分不必要条件,①正确.对于②,开关A闭合,灯泡B不一定亮;而灯泡B亮时,开关A必须闭合,所以开关A闭合是灯泡B亮的必要不充分条件,②正确.对于③,开关A闭合,灯泡B亮;而灯泡B亮时,开关A必须闭合,所以开关A闭合是灯泡B亮的充要条件,③正确.对于④,开关A闭合,灯泡B不一定亮;而灯泡B亮时,开关A不一定闭合,所以开关A闭合是灯泡B亮的既不充分也不必要条件,④错误.
13.解 由已知条件得m≠0.
方程①有实数根的充要条件是Δ=16-4m×4≥0且m≠0,解得m≤1且m≠0.
方程②有实数根的充要条件是Δ=16m2-4(4m2-4m-5)≥0,解得m≥-.所以-≤m≤1且m≠0.
因为m∈Z,所以m=-1或m=1.
当m=-1时,方程①为x2+4x-4=0,无整数根;
当m=1时,方程①为x2-4x+4=0,
方程②为x2-4x-5=0,均有整数根.
所以,方程①和②的根都是整数 m=1;反之,m=1 方程①和②的根都是整数.
故方程①和②的根都是整数的充要条件为m=1.
14.解 △ABC为锐角三角形的充要条件为a2+b2>c2.
证明:充分性:若a2+b2>c2,则△ABC不是直角三角形.
若△ABC为钝角三角形,则∠C>90°,
过点B作AC的延长线的垂线,垂足为D(如图(1)),
由勾股定理知c2=BD2+(b+CD)2=BD2+CD2+b2+2·CD·b=a2+b2+2·CD·b>a2+b2,矛盾,
故△ABC为锐角三角形,充分性成立.
必要性:过点A作边BC的垂线,垂足为D(如图(2)),
由勾股定理知,c2=AD2+BD2=AD2+(a-CD)2=b2-CD2+(a-CD)2=a2+b2-2·CD·a<a2+b2.故必要性成立.
故△ABC为锐角三角形的充要条件为a2+b2>c2.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
