华师版秋学期八年级上册数学《三角形全等判定斜边直角边(HL)》专训(含答案)
文档属性
| 名称 | 华师版秋学期八年级上册数学《三角形全等判定斜边直角边(HL)》专训(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-23 16:36:43 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
华师版秋学期八年级上册数学《三角形全等判定斜边直角边(HL)》专训
一、单选题
1、两个直角三角形全等的条件是( )
A.一锐角对应相等 B.两锐角对应相等 C.一条边对应相等 D.两条边对应相等
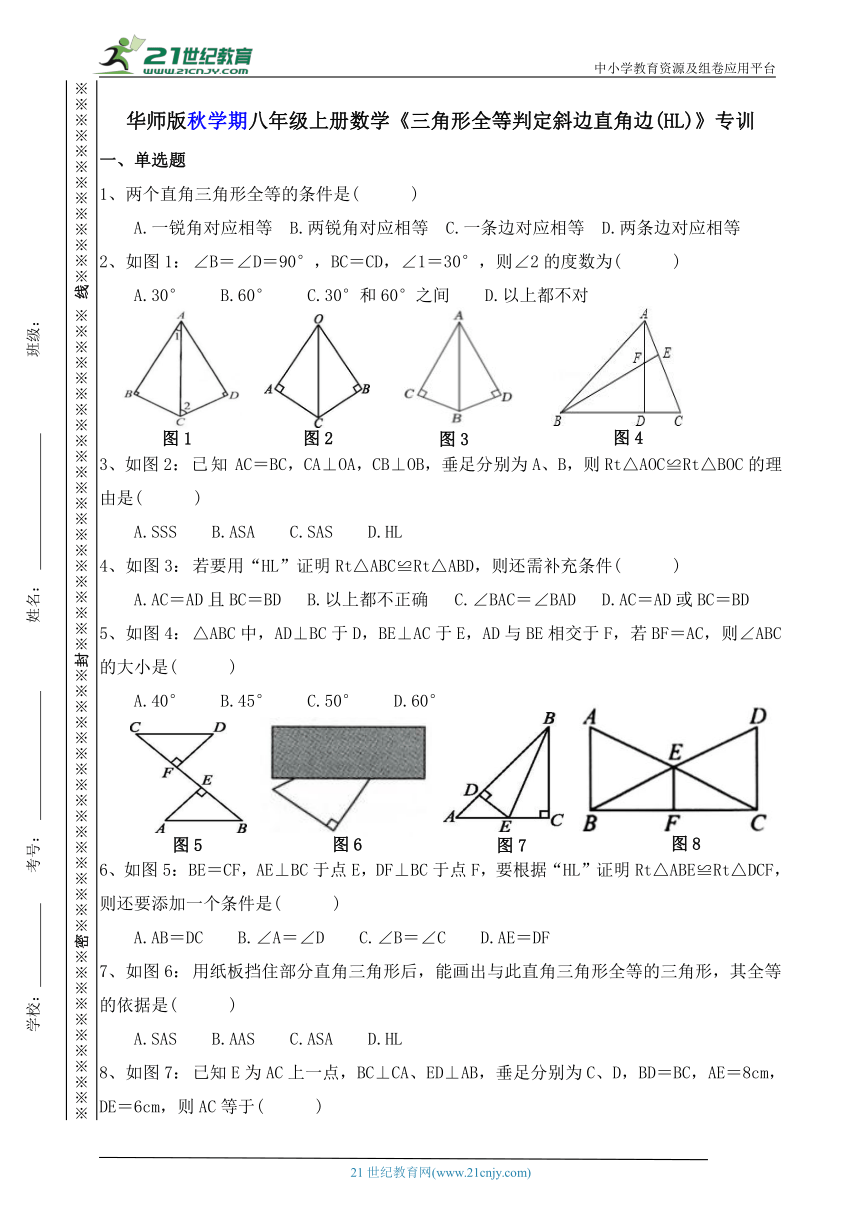
2、如图1:∠B=∠D=90°,BC=CD,∠1=30°,则∠2的度数为( )
A.30° B.60° C.30°和60°之间 D.以上都不对
3、如图2:已知AC=BC,CA⊥OA,CB⊥OB,垂足分别为A、B,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS B.ASA C.SAS D.HL
4、如图3:若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.AC=AD且BC=BD B.以上都不正确 C.∠BAC=∠BAD D.AC=AD或BC=BD
5、如图4:△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( )
A.40° B.45° C.50° D.60°
6、如图5:BE=CF,AE⊥BC于点E,DF⊥BC于点F,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AE=DF
7、如图6:用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( )
A.SAS B.AAS C.ASA D.HL
8、如图7:已知E为AC上一点,BC⊥CA、ED⊥AB,垂足分别为C、D,BD=BC,AE=8cm,DE=6cm,则AC等于( )
A.16cm B.14cm C.12cm D.10cm
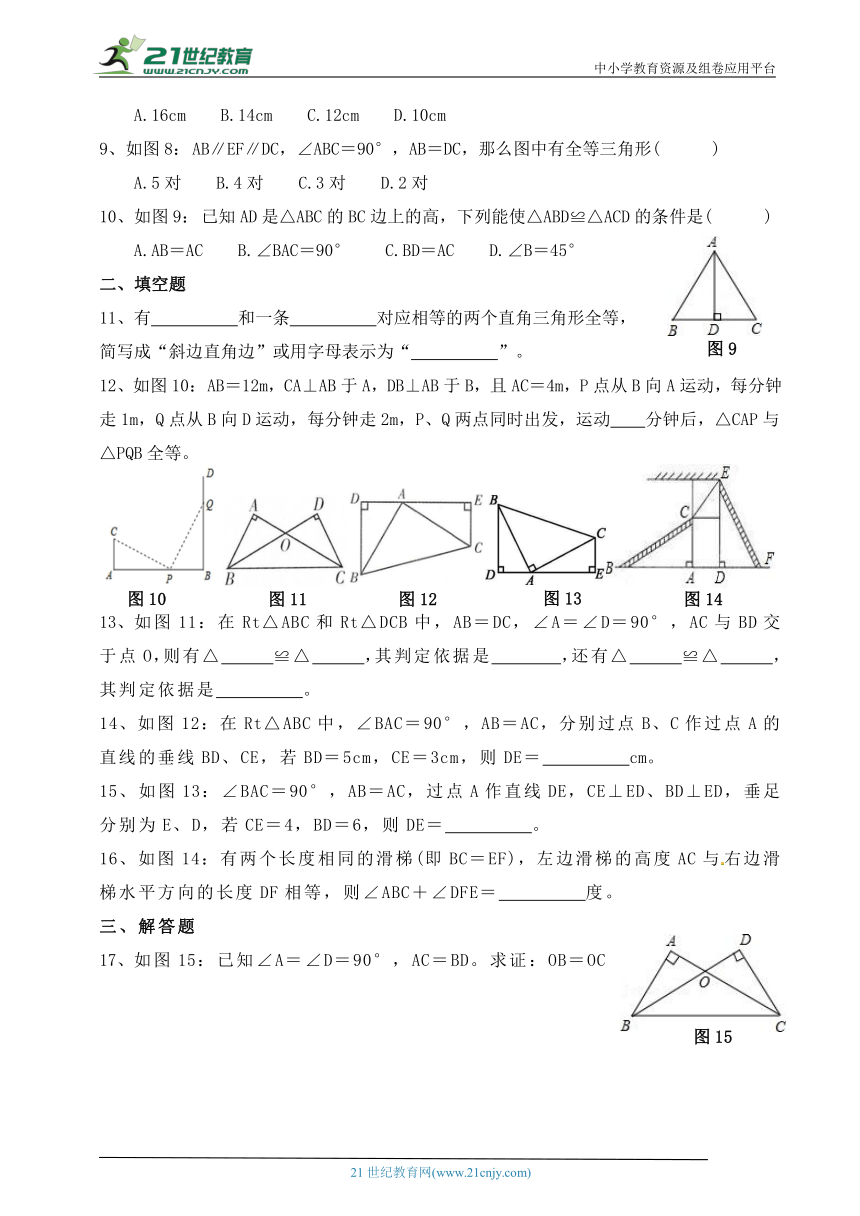
9、如图8:AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( )
A.5对 B.4对 C.3对 D.2对
10、如图9:已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.AB=AC B.∠BAC=90° C.BD=AC D.∠B=45°
二、填空题
11、有 和一条 对应相等的两个直角三角形全等,
简写成“斜边直角边”或用字母表示为“ ”。
12、如图10:AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后,△CAP与△PQB全等。
13、如图11:在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△ ≌△ ,其判定依据是 ,还有△ ≌△ ,其判定依据是 。
14、如图12:在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线BD、CE,若BD=5cm,CE=3cm,则DE= cm。
15、如图13:∠BAC=90°,AB=AC,过点A作直线DE,CE⊥ED、BD⊥ED,垂足分别为E、D,若CE=4,BD=6,则DE= 。
16、如图14:有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度。
三、解答题
17、如图15:已知∠A=∠D=90°,AC=BD。求证:OB=OC
18、如图16:已知AD是△ABC的角平分线,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F。求证:EB=FC
19、如图17:在△ABC中,AB=24,AC=18,AD是BC边上的中线,求线段AD有取值范围?
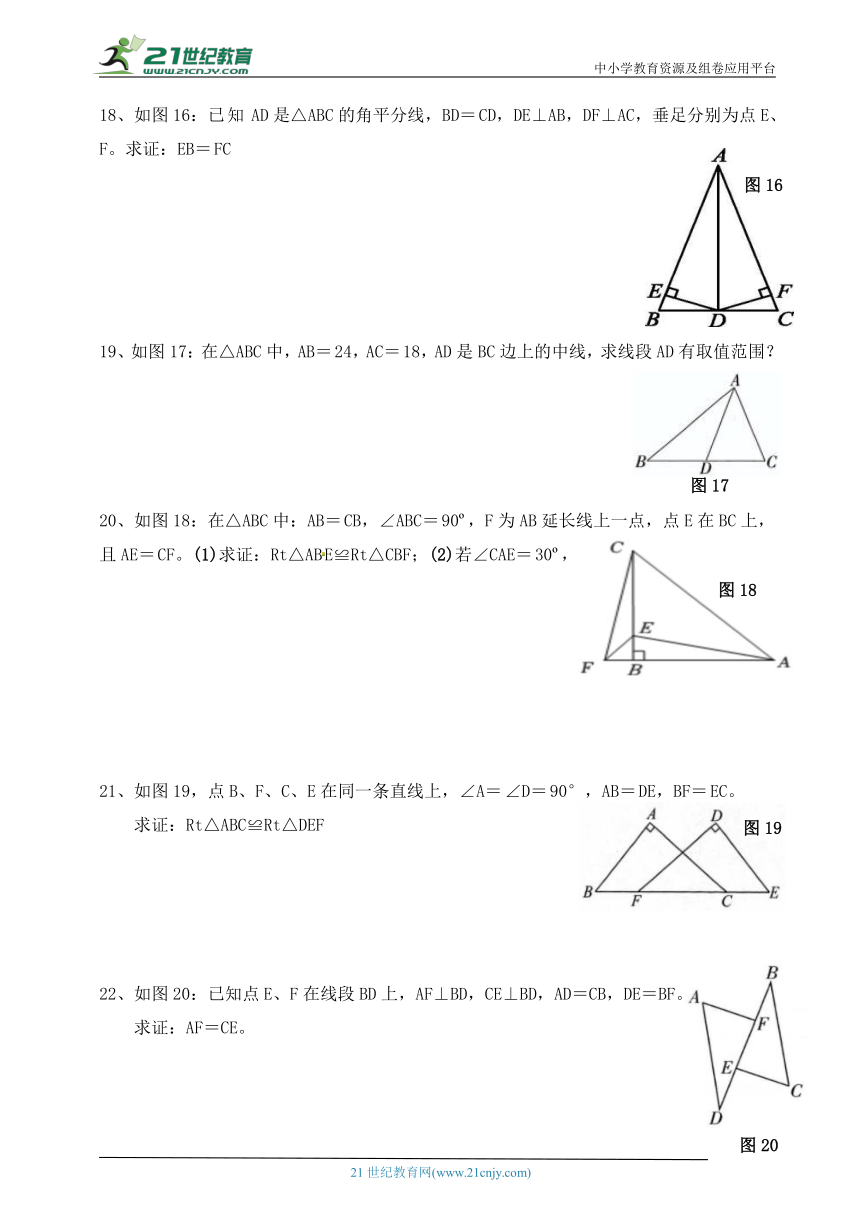
20、如图18:在△ABC中:AB=CB,∠ABC=90 ,F为AB延长线上一点,点E在BC上,且AE=CF。(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30 ,求∠ACF度数。
21、如图19,点B、F、C、E在同一条直线上,∠A=∠D=90°,AB=DE,BF=EC。
求证:Rt△ABC≌Rt△DEF
22、如图20:已知点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF。
求证:AF=CE。
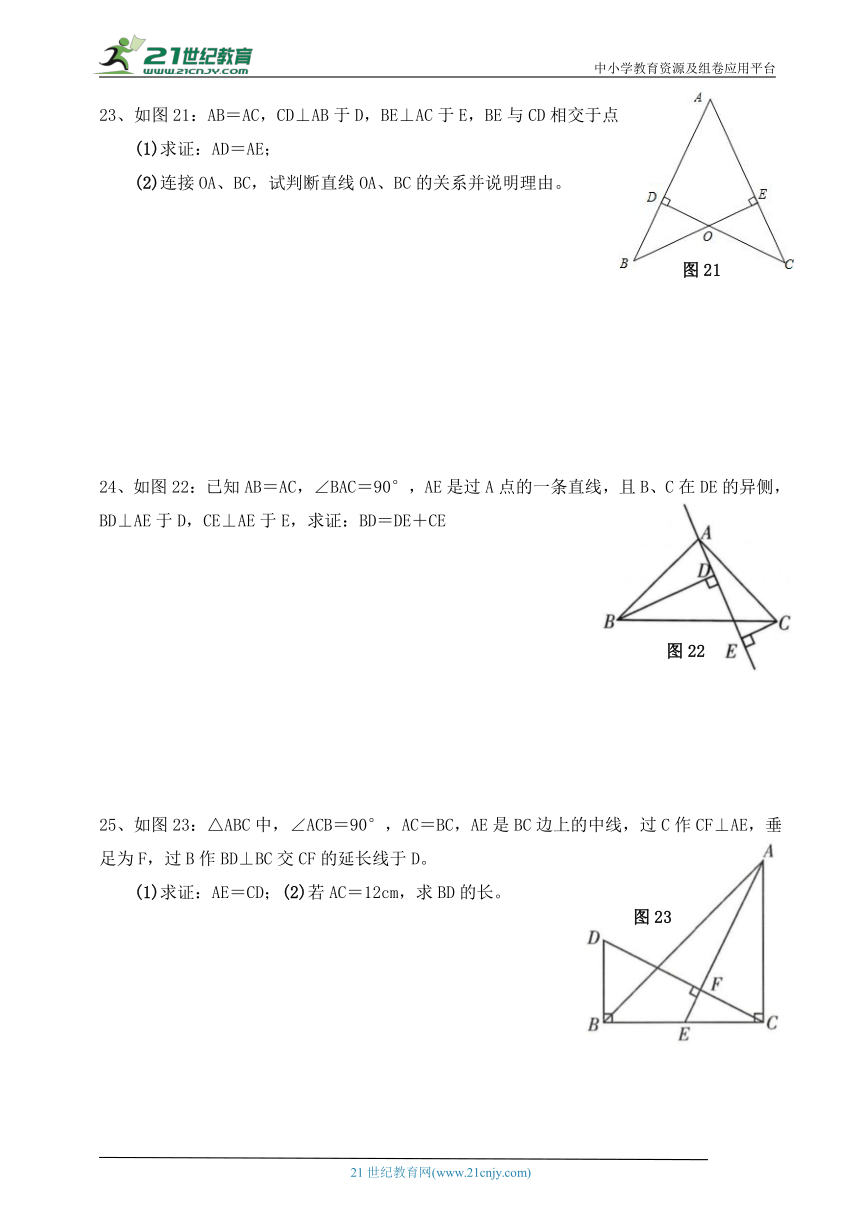
23、如图21:AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O。
(1)求证:AD=AE;
(2)连接OA、BC,试判断直线OA、BC的关系并说明理由。
24、如图22:已知AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE
25、如图23:△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D。
(1)求证:AE=CD;(2)若AC=12cm,求BD的长。
华师版秋学期八年级上册数学《三角形全等判定斜边直角边(HL)》专训答案
一、单选题
1、两个直角三角形全等的条件是( )
A.一锐角对应相等 B.两锐角对应相等 C.一条边对应相等 D.两条边对应相等
答案:D
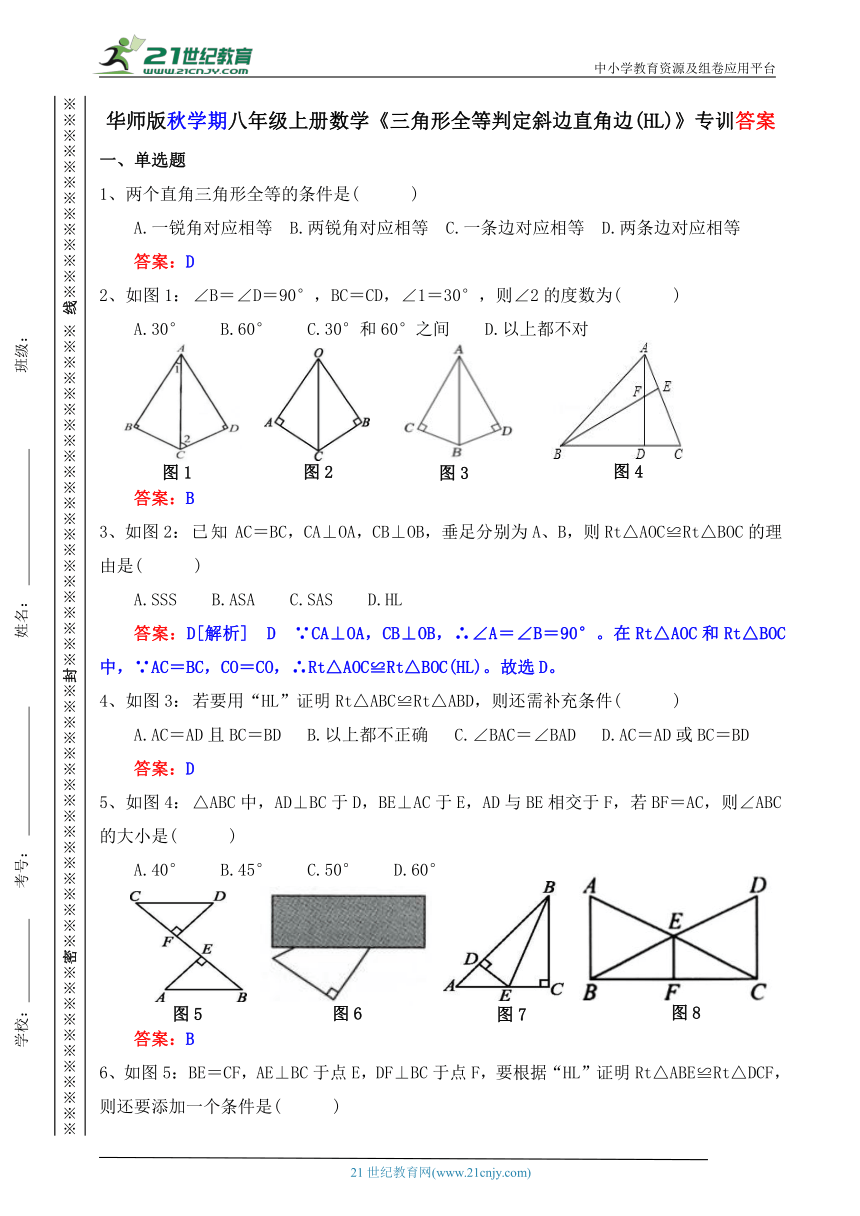
2、如图1:∠B=∠D=90°,BC=CD,∠1=30°,则∠2的度数为( )
A.30° B.60° C.30°和60°之间 D.以上都不对
答案:B
3、如图2:已知AC=BC,CA⊥OA,CB⊥OB,垂足分别为A、B,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS B.ASA C.SAS D.HL
答案:D[解析] D ∵CA⊥OA,CB⊥OB,∴∠A=∠B=90°。在Rt△AOC和Rt△BOC中,∵AC=BC,CO=CO,∴Rt△AOC≌Rt△BOC(HL)。故选D。
4、如图3:若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.AC=AD且BC=BD B.以上都不正确 C.∠BAC=∠BAD D.AC=AD或BC=BD
答案:D
5、如图4:△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( )
A.40° B.45° C.50° D.60°
答案:B
6、如图5:BE=CF,AE⊥BC于点E,DF⊥BC于点F,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AE=DF
答案:A[解析] A 添加条件AB=DC,理由:∵AE⊥BC,DF⊥BC,∴∠CFD=∠BEA=90°,在Rt△ABE和Rt△DCF中,∵AB=DC,BE=CF,∴Rt△ABE≌Rt△DCF(HL)。故选A。
7、如图6:用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( )
A.SAS B.AAS C.ASA D.HL
答案:C
8、如图7:已知E为AC上一点,BC⊥CA、ED⊥AB,垂足分别为C、D,BD=BC,AE=8cm,DE=6cm,则AC等于( )
A.16cm B.14cm C.12cm D.10cm
答案:B[解析]∵BC⊥CA,ED⊥AB,∴∠BDE=∠BCE=90° 在Rt△DEB和Rt△CEB中,∵BE=BE,BD=BC,∴Rt△DEB≌Rt△CEB,∴DE=CE,∴AC=AE+CE=AE+DE=8+6=14(cm)。
9、如图8:AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( )
A.5对 B.4对 C.3对 D.2对
答案:C
10、如图9:已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.AB=AC B.∠BAC=90° C.BD=AC D.∠B=45°
答案:A
二、填空题
11、有 和一条 对应相等的两个直角三角形全等,
简写成“斜边直角边”或用字母表示为“ ”。
答案:斜边 直角边 HL
12、如图10:AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后,△CAP与△PQB全等。
答案:4(分两种情况,有一种情况不全等)
设x分钟后△CAP与△PQB全等,则BP=x,BQ=2x,AQ=12-x
(1)若BP=AC,则x=4 AP=12-4=8,BQ=2x=8 即AP=BP △CAP≌△PBQ
(2)若BP=AP,则12-x=x x=6,BQ=2x=12 即BQ≠AC △CAP和△PBQ不全等。
13、如图11:在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△ ≌△ ,其判定依据是 ,还有△ ≌△ ,其判定依据是 。
答案:ABC DCB HL AOB DOC AAS
14、如图12:在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线BD、CE,若BD=5cm,CE=3cm,则DE= cm。
答案:8
15、如图13:∠BAC=90°,AB=AC,过点A作直线DE,CE⊥ED、BD⊥ED,垂足分别为E、D,若CE=4,BD=6,则DE= 。
答案:10
16、如图14:有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度。
答案:90°(用HL证Rt△ABC≌Rt△DEF得∠ABC=∠DEF 由∠DEF+∠DFE=90得)
三、解答题
17、如图15:已知∠A=∠D=90°,AC=BD。求证:OB=OC
答案:∵ ∠A=∠D=90°
∴ △ABC和△DCB是Rt△
在Rt△ABC和Rt△DCB中:
AC=BD BC=BC
∴ Rt△ABC≌Rt△DCB(HL)
∴ OB=OC
18、如图16:已知AD是△ABC的角平分线,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F。求证:EB=FC
答案:证明:∵ AD是△ABC的角平分线
∴ ∠DAE=∠DAF
∵ DE⊥AB,DF⊥AC
∴ ∠AED=∠AFD=90°
在△AED和△AFD中:
∵ ∠DAE=∠DAF,∠AED=∠AFD,AD=AD
∴ △AED≌△AFD(AAS)
∴ DE=DF
在Rt△DEB和Rt△DFC中:
∵ BD=CD,DE=DF
∴ Rt△DEB≌Rt△DFC(HL)
∴ EB=FC
19、如图17:在△ABC中,AB=24,AC=18,AD是BC边上的中线,求线段AD有取值范围?
答案:解:延长AD至E,使AD=DE,连接BE。
∵ AD是BC边上的中线
∴ BD=CD
在△ACD和△EBD中:
AD=DE ∠1=∠2 BD=CD
∴ △ACD≌△EBD(SAS)
∴ BE=AC=18
在△ABE中:
∵ AB-BE<AE<AB+BE
∴ AB-BE<2AD<AB+BE
∴ 3<AD<21
20、如图18:在△ABC中:AB=CB,∠ABC=90 ,F为AB延长线上一点,点E在BC上,且AE=CF。(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30 ,求∠ACF度数。
答案:解:(1)证明:∵ ∠ABC=90°
∴ ∠CBF=∠ABE=90°
在Rt△ABE和Rt△CBF中:
∵ AE=CF AB=BC ∴Rt△ABE≌Rt△CBF(HL)
(2)∵ AB=BC ∠ABC=90° ∴ ∠CAB=∠ACB=45°
∵ ∠BAE=∠CAB-∠CAE=45°-30°=15°
由(1)知 Rt△ABE≌Rt△CBF ∴∠BCF=∠BAE=15°
∴ ∠ACF=∠BCF+∠ACB=45°+15°=60°
21、如图19,点B、F、C、E在同一条直线上,∠A=∠D=90°,AB=DE,BF=EC。
求证:Rt△ABC≌Rt△DEF
答案:证明:∵ BF=EC
∴ BF+FC=EC+FC 即:BC=EF
∵ ∠A=∠D=90°
∴ △ABC和△DEF都是直角三角形
在Rt△ABC和Rt△DEF中:
∵ AB=DE BC=EF
∴ Rt△ABC≌Rt△DEF(HL)
22、如图20:已知点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF。
求证:AF=CE。
答案:∵ EAF⊥BD CE⊥BD
∴ ∠AFD=∠CEB=90°
∴ △ADF和△CBE是Rt△
∵ DE=BF DF=DE+EF BE=BF+EF
∴ DF=BE
在Rt△ADF和Rt△CBE中:
DF=BE AD=CB
∴ Rt△ADF≌Rt△CBE(HL)
∴ AF=CE
23、如图21:AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O。
(1)求证:AD=AE;
(2)连接OA、BC,试判断直线OA、BC的关系并说明理由。
答案:解:(1)证明:在△ACD与△ABE中:
∵ ∠A=∠A ∠ADC=∠AEB=90° AB=AC
∴ △ACD≌△ABE ∴ AD=AE
(2)互相垂直,理由如下:
在Rt△ADO与△AEO中:
∵ OA=OA AD=AE
∴ △ADO≌△AEO
∴ ∠DAO=∠EAO 即OA是∠BAC的平分线
又∵ AB=AC
∴ OA⊥BC
24、如图22:已知AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE
答案:证明:∵ BD⊥AE于D CE⊥AE于E
∴ ∠ADB=∠AEC=90°
∵ ∠BAC=90°
∴ ∠ABD+∠BAD=∠CAE+∠BAD
∴ ∠ABD=∠CAE
在△ABD和△CAE中:
∠ABD=∠CAE ∠ADB=∠AEC AB=AC
∴ △ABD≌△CAE(AAS)
∴ BD=AE AD=CE
∵ AE=AD+DE
∴ BD=CE+DE
25、如图23:△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D。
(1)求证:AE=CD;(2)若AC=12cm,求BD的长。
答案:解:(1)证明:∵ CF⊥AE BD⊥BC
∴ ∠EFC=∠DBC=90°
∴ ∠1+∠2=∠1+∠D=90° +
∴ ∠2=∠D(同理∠3=∠1)
∵ ∠ACB=90°
∴ ∠DBC=∠ECA=90°
在△DBC和△ECA中:
∠2=∠D ∠DBC=∠ECA BC=AC
∴ △DBC≌△ECA(AAS)(也可用ASA)
∴ AE=CD
(2)由(1)知:△DBC≌△ECA
∴ BD=CE
∵ AE是BC边上的中线 ∴ CE=0.5BC
∵ AC=BC=12cm
∴ BD=CE=0.5BC=0.5AC=6cm
学校: 考号: 姓名: 班级:
※※※※※※※※※※※密※※※※※※※※※※※※※※※※※封※※※※※※※※※※※※※※※※※※※※※※ 线※※※※※※※※※※※※※
图3
图4
图2
图1
图7
图8
图6
图5
图9
图14
图13
图12
图11
图10
图15
图16
图17
图18
图19
图20
图21
图22
图23
学校: 考号: 姓名: 班级:
※※※※※※※※※※※密※※※※※※※※※※※※※※※※※封※※※※※※※※※※※※※※※※※※※※※※ 线※※※※※※※※※※※※※
图3
图4
图2
图1
图7
图8
图6
图5
图9
图14
图13
图12
图11
图10
图15
图16
图17
图18
图19
图20
图21
图22
图23
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
华师版秋学期八年级上册数学《三角形全等判定斜边直角边(HL)》专训
一、单选题
1、两个直角三角形全等的条件是( )
A.一锐角对应相等 B.两锐角对应相等 C.一条边对应相等 D.两条边对应相等
2、如图1:∠B=∠D=90°,BC=CD,∠1=30°,则∠2的度数为( )
A.30° B.60° C.30°和60°之间 D.以上都不对
3、如图2:已知AC=BC,CA⊥OA,CB⊥OB,垂足分别为A、B,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS B.ASA C.SAS D.HL
4、如图3:若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.AC=AD且BC=BD B.以上都不正确 C.∠BAC=∠BAD D.AC=AD或BC=BD
5、如图4:△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( )
A.40° B.45° C.50° D.60°
6、如图5:BE=CF,AE⊥BC于点E,DF⊥BC于点F,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AE=DF
7、如图6:用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( )
A.SAS B.AAS C.ASA D.HL
8、如图7:已知E为AC上一点,BC⊥CA、ED⊥AB,垂足分别为C、D,BD=BC,AE=8cm,DE=6cm,则AC等于( )
A.16cm B.14cm C.12cm D.10cm
9、如图8:AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( )
A.5对 B.4对 C.3对 D.2对
10、如图9:已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.AB=AC B.∠BAC=90° C.BD=AC D.∠B=45°
二、填空题
11、有 和一条 对应相等的两个直角三角形全等,
简写成“斜边直角边”或用字母表示为“ ”。
12、如图10:AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后,△CAP与△PQB全等。
13、如图11:在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△ ≌△ ,其判定依据是 ,还有△ ≌△ ,其判定依据是 。
14、如图12:在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线BD、CE,若BD=5cm,CE=3cm,则DE= cm。
15、如图13:∠BAC=90°,AB=AC,过点A作直线DE,CE⊥ED、BD⊥ED,垂足分别为E、D,若CE=4,BD=6,则DE= 。
16、如图14:有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度。
三、解答题
17、如图15:已知∠A=∠D=90°,AC=BD。求证:OB=OC
18、如图16:已知AD是△ABC的角平分线,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F。求证:EB=FC
19、如图17:在△ABC中,AB=24,AC=18,AD是BC边上的中线,求线段AD有取值范围?
20、如图18:在△ABC中:AB=CB,∠ABC=90 ,F为AB延长线上一点,点E在BC上,且AE=CF。(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30 ,求∠ACF度数。
21、如图19,点B、F、C、E在同一条直线上,∠A=∠D=90°,AB=DE,BF=EC。
求证:Rt△ABC≌Rt△DEF
22、如图20:已知点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF。
求证:AF=CE。
23、如图21:AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O。
(1)求证:AD=AE;
(2)连接OA、BC,试判断直线OA、BC的关系并说明理由。
24、如图22:已知AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE
25、如图23:△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D。
(1)求证:AE=CD;(2)若AC=12cm,求BD的长。
华师版秋学期八年级上册数学《三角形全等判定斜边直角边(HL)》专训答案
一、单选题
1、两个直角三角形全等的条件是( )
A.一锐角对应相等 B.两锐角对应相等 C.一条边对应相等 D.两条边对应相等
答案:D
2、如图1:∠B=∠D=90°,BC=CD,∠1=30°,则∠2的度数为( )
A.30° B.60° C.30°和60°之间 D.以上都不对
答案:B
3、如图2:已知AC=BC,CA⊥OA,CB⊥OB,垂足分别为A、B,则Rt△AOC≌Rt△BOC的理由是( )
A.SSS B.ASA C.SAS D.HL
答案:D[解析] D ∵CA⊥OA,CB⊥OB,∴∠A=∠B=90°。在Rt△AOC和Rt△BOC中,∵AC=BC,CO=CO,∴Rt△AOC≌Rt△BOC(HL)。故选D。
4、如图3:若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.AC=AD且BC=BD B.以上都不正确 C.∠BAC=∠BAD D.AC=AD或BC=BD
答案:D
5、如图4:△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是( )
A.40° B.45° C.50° D.60°
答案:B
6、如图5:BE=CF,AE⊥BC于点E,DF⊥BC于点F,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AE=DF
答案:A[解析] A 添加条件AB=DC,理由:∵AE⊥BC,DF⊥BC,∴∠CFD=∠BEA=90°,在Rt△ABE和Rt△DCF中,∵AB=DC,BE=CF,∴Rt△ABE≌Rt△DCF(HL)。故选A。
7、如图6:用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( )
A.SAS B.AAS C.ASA D.HL
答案:C
8、如图7:已知E为AC上一点,BC⊥CA、ED⊥AB,垂足分别为C、D,BD=BC,AE=8cm,DE=6cm,则AC等于( )
A.16cm B.14cm C.12cm D.10cm
答案:B[解析]∵BC⊥CA,ED⊥AB,∴∠BDE=∠BCE=90° 在Rt△DEB和Rt△CEB中,∵BE=BE,BD=BC,∴Rt△DEB≌Rt△CEB,∴DE=CE,∴AC=AE+CE=AE+DE=8+6=14(cm)。
9、如图8:AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( )
A.5对 B.4对 C.3对 D.2对
答案:C
10、如图9:已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.AB=AC B.∠BAC=90° C.BD=AC D.∠B=45°
答案:A
二、填空题
11、有 和一条 对应相等的两个直角三角形全等,
简写成“斜边直角边”或用字母表示为“ ”。
答案:斜边 直角边 HL
12、如图10:AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后,△CAP与△PQB全等。
答案:4(分两种情况,有一种情况不全等)
设x分钟后△CAP与△PQB全等,则BP=x,BQ=2x,AQ=12-x
(1)若BP=AC,则x=4 AP=12-4=8,BQ=2x=8 即AP=BP △CAP≌△PBQ
(2)若BP=AP,则12-x=x x=6,BQ=2x=12 即BQ≠AC △CAP和△PBQ不全等。
13、如图11:在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△ ≌△ ,其判定依据是 ,还有△ ≌△ ,其判定依据是 。
答案:ABC DCB HL AOB DOC AAS
14、如图12:在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线BD、CE,若BD=5cm,CE=3cm,则DE= cm。
答案:8
15、如图13:∠BAC=90°,AB=AC,过点A作直线DE,CE⊥ED、BD⊥ED,垂足分别为E、D,若CE=4,BD=6,则DE= 。
答案:10
16、如图14:有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度。
答案:90°(用HL证Rt△ABC≌Rt△DEF得∠ABC=∠DEF 由∠DEF+∠DFE=90得)
三、解答题
17、如图15:已知∠A=∠D=90°,AC=BD。求证:OB=OC
答案:∵ ∠A=∠D=90°
∴ △ABC和△DCB是Rt△
在Rt△ABC和Rt△DCB中:
AC=BD BC=BC
∴ Rt△ABC≌Rt△DCB(HL)
∴ OB=OC
18、如图16:已知AD是△ABC的角平分线,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F。求证:EB=FC
答案:证明:∵ AD是△ABC的角平分线
∴ ∠DAE=∠DAF
∵ DE⊥AB,DF⊥AC
∴ ∠AED=∠AFD=90°
在△AED和△AFD中:
∵ ∠DAE=∠DAF,∠AED=∠AFD,AD=AD
∴ △AED≌△AFD(AAS)
∴ DE=DF
在Rt△DEB和Rt△DFC中:
∵ BD=CD,DE=DF
∴ Rt△DEB≌Rt△DFC(HL)
∴ EB=FC
19、如图17:在△ABC中,AB=24,AC=18,AD是BC边上的中线,求线段AD有取值范围?
答案:解:延长AD至E,使AD=DE,连接BE。
∵ AD是BC边上的中线
∴ BD=CD
在△ACD和△EBD中:
AD=DE ∠1=∠2 BD=CD
∴ △ACD≌△EBD(SAS)
∴ BE=AC=18
在△ABE中:
∵ AB-BE<AE<AB+BE
∴ AB-BE<2AD<AB+BE
∴ 3<AD<21
20、如图18:在△ABC中:AB=CB,∠ABC=90 ,F为AB延长线上一点,点E在BC上,且AE=CF。(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30 ,求∠ACF度数。
答案:解:(1)证明:∵ ∠ABC=90°
∴ ∠CBF=∠ABE=90°
在Rt△ABE和Rt△CBF中:
∵ AE=CF AB=BC ∴Rt△ABE≌Rt△CBF(HL)
(2)∵ AB=BC ∠ABC=90° ∴ ∠CAB=∠ACB=45°
∵ ∠BAE=∠CAB-∠CAE=45°-30°=15°
由(1)知 Rt△ABE≌Rt△CBF ∴∠BCF=∠BAE=15°
∴ ∠ACF=∠BCF+∠ACB=45°+15°=60°
21、如图19,点B、F、C、E在同一条直线上,∠A=∠D=90°,AB=DE,BF=EC。
求证:Rt△ABC≌Rt△DEF
答案:证明:∵ BF=EC
∴ BF+FC=EC+FC 即:BC=EF
∵ ∠A=∠D=90°
∴ △ABC和△DEF都是直角三角形
在Rt△ABC和Rt△DEF中:
∵ AB=DE BC=EF
∴ Rt△ABC≌Rt△DEF(HL)
22、如图20:已知点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF。
求证:AF=CE。
答案:∵ EAF⊥BD CE⊥BD
∴ ∠AFD=∠CEB=90°
∴ △ADF和△CBE是Rt△
∵ DE=BF DF=DE+EF BE=BF+EF
∴ DF=BE
在Rt△ADF和Rt△CBE中:
DF=BE AD=CB
∴ Rt△ADF≌Rt△CBE(HL)
∴ AF=CE
23、如图21:AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O。
(1)求证:AD=AE;
(2)连接OA、BC,试判断直线OA、BC的关系并说明理由。
答案:解:(1)证明:在△ACD与△ABE中:
∵ ∠A=∠A ∠ADC=∠AEB=90° AB=AC
∴ △ACD≌△ABE ∴ AD=AE
(2)互相垂直,理由如下:
在Rt△ADO与△AEO中:
∵ OA=OA AD=AE
∴ △ADO≌△AEO
∴ ∠DAO=∠EAO 即OA是∠BAC的平分线
又∵ AB=AC
∴ OA⊥BC
24、如图22:已知AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE
答案:证明:∵ BD⊥AE于D CE⊥AE于E
∴ ∠ADB=∠AEC=90°
∵ ∠BAC=90°
∴ ∠ABD+∠BAD=∠CAE+∠BAD
∴ ∠ABD=∠CAE
在△ABD和△CAE中:
∠ABD=∠CAE ∠ADB=∠AEC AB=AC
∴ △ABD≌△CAE(AAS)
∴ BD=AE AD=CE
∵ AE=AD+DE
∴ BD=CE+DE
25、如图23:△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D。
(1)求证:AE=CD;(2)若AC=12cm,求BD的长。
答案:解:(1)证明:∵ CF⊥AE BD⊥BC
∴ ∠EFC=∠DBC=90°
∴ ∠1+∠2=∠1+∠D=90° +
∴ ∠2=∠D(同理∠3=∠1)
∵ ∠ACB=90°
∴ ∠DBC=∠ECA=90°
在△DBC和△ECA中:
∠2=∠D ∠DBC=∠ECA BC=AC
∴ △DBC≌△ECA(AAS)(也可用ASA)
∴ AE=CD
(2)由(1)知:△DBC≌△ECA
∴ BD=CE
∵ AE是BC边上的中线 ∴ CE=0.5BC
∵ AC=BC=12cm
∴ BD=CE=0.5BC=0.5AC=6cm
学校: 考号: 姓名: 班级:
※※※※※※※※※※※密※※※※※※※※※※※※※※※※※封※※※※※※※※※※※※※※※※※※※※※※ 线※※※※※※※※※※※※※
图3
图4
图2
图1
图7
图8
图6
图5
图9
图14
图13
图12
图11
图10
图15
图16
图17
图18
图19
图20
图21
图22
图23
学校: 考号: 姓名: 班级:
※※※※※※※※※※※密※※※※※※※※※※※※※※※※※封※※※※※※※※※※※※※※※※※※※※※※ 线※※※※※※※※※※※※※
图3
图4
图2
图1
图7
图8
图6
图5
图9
图14
图13
图12
图11
图10
图15
图16
图17
图18
图19
图20
图21
图22
图23
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
