人教版数学九年级上册 24.4 弧长及扇形面积公式 教学设计
文档属性
| 名称 | 人教版数学九年级上册 24.4 弧长及扇形面积公式 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 14:04:16 | ||
图片预览



文档简介
24.4 弧长和扇形面积
教学目标:
1、经历弧长公式和扇形面积公式的推导过程,能运用弧长公式和扇形面积公式进行有关计算.
2、通过弧长和扇形面积公式的推导过程与运用,发展学生分析问题、解决问题及计算的能力.
3、通过弧长公式和扇形面积公式的推导,发展学生抽象、理解、概括、归纳能力和迁移能力.
重点:弧长,扇形面积公式的导出及应用.
难点:对图形的分析
教学过程:
活动一:创设情境,引入课题
问题1 如图,在运动会的400米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
,.
设计意图:从现实生活中创设情境,有助于激发学生的求知欲,提高学生的学习兴趣。
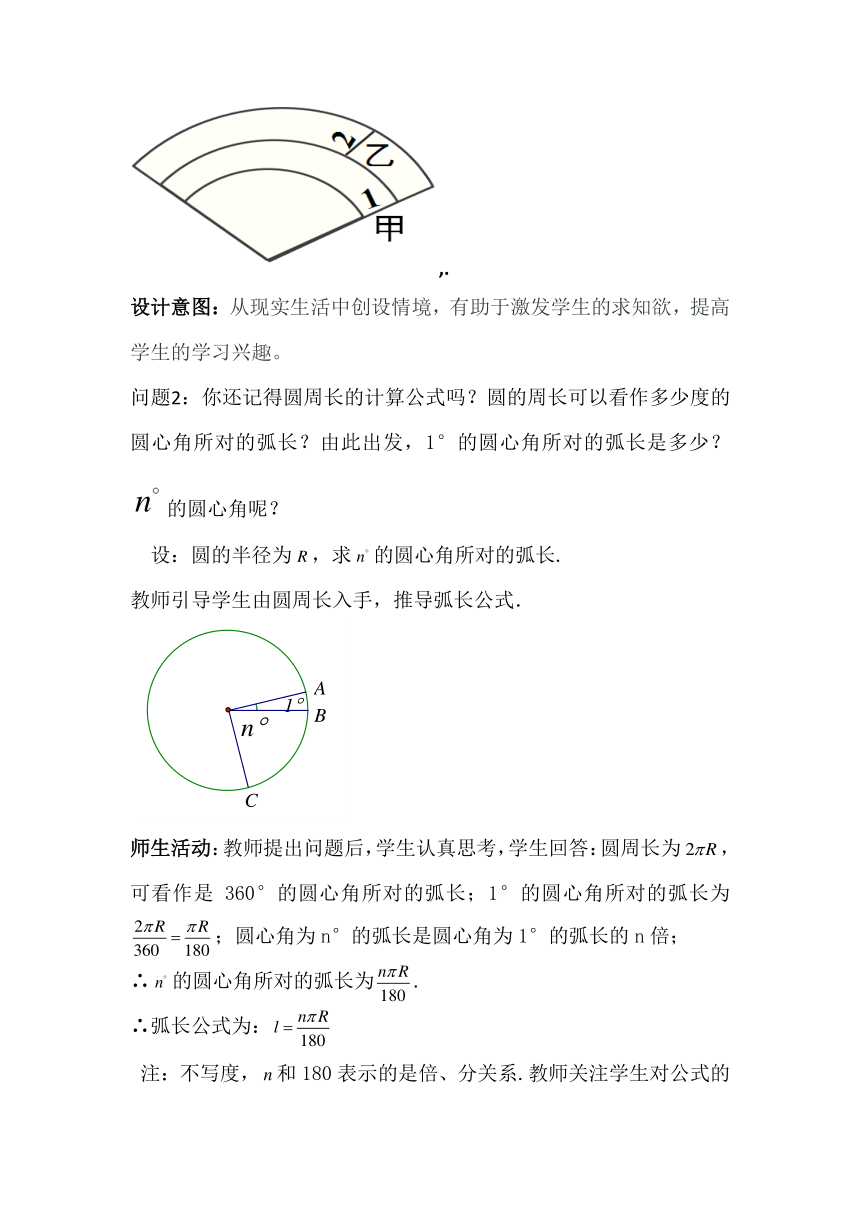
问题2:你还记得圆周长的计算公式吗?圆的周长可以看作多少度的圆心角所对的弧长?由此出发,1°的圆心角所对的弧长是多少?的圆心角呢?
设:圆的半径为,求的圆心角所对的弧长.
教师引导学生由圆周长入手,推导弧长公式.
师生活动:教师提出问题后,学生认真思考,学生回答:圆周长为,可看作是360°的圆心角所对的弧长;1°的圆心角所对的弧长为;圆心角为n°的弧长是圆心角为1°的弧长的n倍;
∴的圆心角所对的弧长为.
∴弧长公式为:
注:不写度,和180表示的是倍、分关系.教师关注学生对公式的理解程度.
设计意图:在教师的引导下,教师引导学生由圆周长入手,推导弧长公式.使学生明确公式的推导过程,知道公式的来龙去脉,更要学会学习新知识的方法.
活动二:例题精讲,公式应用:
1、制造弯形管道时,经常要先按中心线计算“展直长度”(图1中虚线的长度),再下料,这就涉及到计算弧长的问题.
(
图1
)
师生活动:教师提出问题后,学生认真思考,说明解题的关键是求中心线“展直长度”,但如何求呢?由弧长公式,就可以得出弧AB的长:
因此所要求的展直长度
2×700+1570=2970
∴所要求的展直长度约为2970mm.
设计意图:数学知识来源于生活实际,又用来解决实际中的问题,强化数学的应用意识.
活动2:比一比,看谁算得快?
练习:
1.半径为4,80°的圆心角所对的弧长为 ;
2.扇形的弧长为,半径为3,则其面积为 ;
3.扇形的半径为24,面积为240,则这个扇形的圆心角
师生活动: 教师提出问题后,学生认真思考,独立完成,看谁最先做好.
设计意图: 迅速、正确的运用所学公式解题,培养学生良好的学习习惯,训练学生的解题速度.
概念学习: 扇形
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫作扇形.
师生活动:强调扇形的特征,由两条半径和一条弧围成的图形。
用来判断扇形。
问题3:你还记得圆面积的计算公式吗?圆面积可以看作多少度的圆心角所对的扇形的面积?1°的圆心角所对的扇形面积是多少?的圆心角呢?
设:已知⊙O半径为,求的圆心角所对的扇形面积.
(2)圆的面积可以看作是多少度的圆心角所对的面积?
(3)1°的圆心角所对的面积是多少?2°呢?
3°呢?…n°呢?
师生活动:教师引导学生类比弧长公式的推导过程,推导出扇形面
积公式:
(1)圆面积S=πR2,可以看作是360°的圆心角所对的扇形面积;
(2)圆心角为1°的扇形的面积=.
(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积n倍;
∴扇形面积公式为
设计意图:让学生模仿弧长的推导过程,再次体会部分和整体之间的关系,同时也培养了学生动手、动脑以及与他人合作交流的能力
问题4:比较扇形面积公式和弧长公式,看看它们之间有什么关系
师生活动:经过观察,学生能够看出:
,其中,是扇形的弧长,为半径.
活动五:例题分析
如图2,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积(精确到0.012m)
师生活动:经过分析,学生知道了水面高即弧AB中点到弦AB的距离.
因此想到做辅助线的方法:连接OA、AB,过O作OC⊥AB于点D,交弧AB于点C. 教师关注学生对题目的理解,师生共同分析题目条件后,由学生独立写出解题过程,展示学生的解题过程,再由学生对解题过程给予评价.
设计意图:培养学生综合运用知识解题的能力.学生在学习新知识的同时要想到学过的知识,在这里就运用了垂径定理.
(例题变式题)如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
师生活动:发展学生的解决实际问题的能力和应用意识.初步探索建立数学模型.让学生畅所欲言,教师了解学生的学习情况,并让学生逐渐的学会总结。检查知识的落实性,以便发现问题和及时解决问题。继续培养学生的探究意识和学习上持之以恒的精神.
活动六:例题分析
正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形,求树叶图案的面积:
设计意图:检查知识的落实性,以便发现问题和及时解决问题。
继续培养学生的探究意识和学习上持之以恒的精神.
活动六:理一理
学生小结
师生活动:由学生谈谈本节课学习的体会和收获,各抒己见.教师对学生的回答给予帮助,让语言表达更准确.
知识:弧长公式;
扇形面积公式:.
能力:灵活运用公式解决实际问题.
活动七:课后作业:
1、课本p59:1,2。
师生活动:学生课下独立完成,教师对学生的作业在批改后及时反馈.
设计意图:检查知识的落实性,以便发现问题和及时解决问题。继续培养学生的探究意识和学习上持之以恒的精神.
板书设计
弧长公式: 例题分析
扇形面积公式:
教学目标:
1、经历弧长公式和扇形面积公式的推导过程,能运用弧长公式和扇形面积公式进行有关计算.
2、通过弧长和扇形面积公式的推导过程与运用,发展学生分析问题、解决问题及计算的能力.
3、通过弧长公式和扇形面积公式的推导,发展学生抽象、理解、概括、归纳能力和迁移能力.
重点:弧长,扇形面积公式的导出及应用.
难点:对图形的分析
教学过程:
活动一:创设情境,引入课题
问题1 如图,在运动会的400米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
,.
设计意图:从现实生活中创设情境,有助于激发学生的求知欲,提高学生的学习兴趣。
问题2:你还记得圆周长的计算公式吗?圆的周长可以看作多少度的圆心角所对的弧长?由此出发,1°的圆心角所对的弧长是多少?的圆心角呢?
设:圆的半径为,求的圆心角所对的弧长.
教师引导学生由圆周长入手,推导弧长公式.
师生活动:教师提出问题后,学生认真思考,学生回答:圆周长为,可看作是360°的圆心角所对的弧长;1°的圆心角所对的弧长为;圆心角为n°的弧长是圆心角为1°的弧长的n倍;
∴的圆心角所对的弧长为.
∴弧长公式为:
注:不写度,和180表示的是倍、分关系.教师关注学生对公式的理解程度.
设计意图:在教师的引导下,教师引导学生由圆周长入手,推导弧长公式.使学生明确公式的推导过程,知道公式的来龙去脉,更要学会学习新知识的方法.
活动二:例题精讲,公式应用:
1、制造弯形管道时,经常要先按中心线计算“展直长度”(图1中虚线的长度),再下料,这就涉及到计算弧长的问题.
(
图1
)
师生活动:教师提出问题后,学生认真思考,说明解题的关键是求中心线“展直长度”,但如何求呢?由弧长公式,就可以得出弧AB的长:
因此所要求的展直长度
2×700+1570=2970
∴所要求的展直长度约为2970mm.
设计意图:数学知识来源于生活实际,又用来解决实际中的问题,强化数学的应用意识.
活动2:比一比,看谁算得快?
练习:
1.半径为4,80°的圆心角所对的弧长为 ;
2.扇形的弧长为,半径为3,则其面积为 ;
3.扇形的半径为24,面积为240,则这个扇形的圆心角
师生活动: 教师提出问题后,学生认真思考,独立完成,看谁最先做好.
设计意图: 迅速、正确的运用所学公式解题,培养学生良好的学习习惯,训练学生的解题速度.
概念学习: 扇形
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫作扇形.
师生活动:强调扇形的特征,由两条半径和一条弧围成的图形。
用来判断扇形。
问题3:你还记得圆面积的计算公式吗?圆面积可以看作多少度的圆心角所对的扇形的面积?1°的圆心角所对的扇形面积是多少?的圆心角呢?
设:已知⊙O半径为,求的圆心角所对的扇形面积.
(2)圆的面积可以看作是多少度的圆心角所对的面积?
(3)1°的圆心角所对的面积是多少?2°呢?
3°呢?…n°呢?
师生活动:教师引导学生类比弧长公式的推导过程,推导出扇形面
积公式:
(1)圆面积S=πR2,可以看作是360°的圆心角所对的扇形面积;
(2)圆心角为1°的扇形的面积=.
(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积n倍;
∴扇形面积公式为
设计意图:让学生模仿弧长的推导过程,再次体会部分和整体之间的关系,同时也培养了学生动手、动脑以及与他人合作交流的能力
问题4:比较扇形面积公式和弧长公式,看看它们之间有什么关系
师生活动:经过观察,学生能够看出:
,其中,是扇形的弧长,为半径.
活动五:例题分析
如图2,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积(精确到0.012m)
师生活动:经过分析,学生知道了水面高即弧AB中点到弦AB的距离.
因此想到做辅助线的方法:连接OA、AB,过O作OC⊥AB于点D,交弧AB于点C. 教师关注学生对题目的理解,师生共同分析题目条件后,由学生独立写出解题过程,展示学生的解题过程,再由学生对解题过程给予评价.
设计意图:培养学生综合运用知识解题的能力.学生在学习新知识的同时要想到学过的知识,在这里就运用了垂径定理.
(例题变式题)如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
师生活动:发展学生的解决实际问题的能力和应用意识.初步探索建立数学模型.让学生畅所欲言,教师了解学生的学习情况,并让学生逐渐的学会总结。检查知识的落实性,以便发现问题和及时解决问题。继续培养学生的探究意识和学习上持之以恒的精神.
活动六:例题分析
正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形,求树叶图案的面积:
设计意图:检查知识的落实性,以便发现问题和及时解决问题。
继续培养学生的探究意识和学习上持之以恒的精神.
活动六:理一理
学生小结
师生活动:由学生谈谈本节课学习的体会和收获,各抒己见.教师对学生的回答给予帮助,让语言表达更准确.
知识:弧长公式;
扇形面积公式:.
能力:灵活运用公式解决实际问题.
活动七:课后作业:
1、课本p59:1,2。
师生活动:学生课下独立完成,教师对学生的作业在批改后及时反馈.
设计意图:检查知识的落实性,以便发现问题和及时解决问题。继续培养学生的探究意识和学习上持之以恒的精神.
板书设计
弧长公式: 例题分析
扇形面积公式:
同课章节目录
