3.1.2 椭圆的简单几何性质(一)学案(无答案)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.1.2 椭圆的简单几何性质(一)学案(无答案)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册 |
|
|
| 格式 | docx | ||
| 文件大小 | 103.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-23 00:00:00 | ||
图片预览

文档简介
课题:第三章 圆锥曲线的方程
3.1.2 椭圆的几何性质(一)
班级—————— 姓名——————
一、学习目标
1.根据椭圆的方程研究椭圆的几何性质,并正确地画出它的图形;
2.了解离心率对椭圆扁平程度的影响,掌握椭圆标准方程中,b,c,e之间的相互关系。
二、问题与例题
思考:与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标准方程研究椭圆的几何性质。
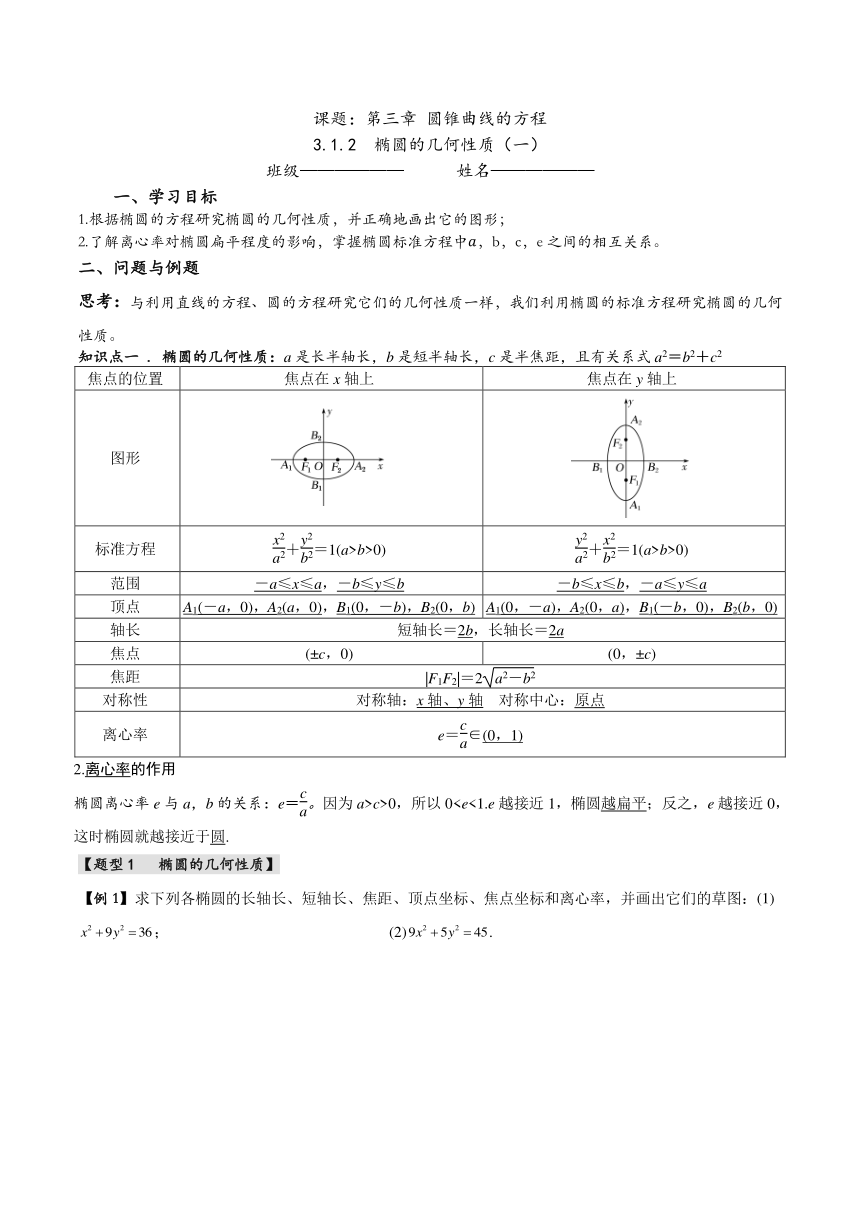
知识点一 . 椭圆的几何性质:a是长半轴长,b是短半轴长,c是半焦距,且有关系式a2=b2+c2
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准方程 +=1(a>b>0) +=1(a>b>0)
范围 -a≤x≤a,-b≤y≤b -b≤x≤b,-a≤y≤a
顶点 A1(-a,0),A2(a,0),B1(0,-b),B2(0,b) A1(0,-a),A2(0,a),B1(-b,0),B2(b,0)
轴长 短轴长=2b,长轴长=2a
焦点 (±c,0) (0,±c)
焦距 |F1F2|=2
对称性 对称轴:x轴、y轴 对称中心:原点
离心率 e=∈(0,1)
2.离心率的作用
椭圆离心率e与a,b的关系:e=。因为a>c>0,所以0【题型1 椭圆的几何性质】
【例1】求下列各椭圆的长轴长、短轴长、焦距、顶点坐标、焦点坐标和离心率,并画出它们的草图:(1); (2).
【变式1-1】求适合下列条件的椭圆的标准方程:
(1)长轴长为6,离心率为; (2)经过点,离心率为,焦点在x轴上;
(3)x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
【题型2 椭圆的离心率】
【例2】下列方程表示的椭圆中,形状最接近圆的是( )
A. B. C. D.
【变式2-1】已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若椭圆C的中心到直线AB的距离为|F1F2|,则椭圆C的离心率 .
【变式2-2】设,是椭圆()的左、右焦点,过的直线与交于,两点,若,,则的离心率为( ) A. B. C. D.
【变式2-3】椭圆的左右焦点分别为,点,线段,分别交于两点,过点作的切线交于,且,则的离心率为( )
A. B. C. D.
目标检测
1.椭圆+=1的长轴长为( )A.2 B.4 C.3 D.6
2.如图,直线l:x-2y+2=0过椭圆+=1(a>b>0)的左焦点F1和一个顶点B,该椭圆的离心率为( )A. B. C. D.
3.已知中心在原点的椭圆C的右焦点为F(1,0),离心率等于,则C的方程是( )
A.+=1 B.+=1 C.+=1 D.+y2=1
4.若一个椭圆的长轴长与焦距的和等于短轴长的2倍,则该椭圆的离心率是( )A. B. C. D.
5.若焦点在y轴上的椭圆+=1的离心率为,则m的值为________.
3.1.2 椭圆的几何性质(一)
班级—————— 姓名——————
一、学习目标
1.根据椭圆的方程研究椭圆的几何性质,并正确地画出它的图形;
2.了解离心率对椭圆扁平程度的影响,掌握椭圆标准方程中,b,c,e之间的相互关系。
二、问题与例题
思考:与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标准方程研究椭圆的几何性质。
知识点一 . 椭圆的几何性质:a是长半轴长,b是短半轴长,c是半焦距,且有关系式a2=b2+c2
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准方程 +=1(a>b>0) +=1(a>b>0)
范围 -a≤x≤a,-b≤y≤b -b≤x≤b,-a≤y≤a
顶点 A1(-a,0),A2(a,0),B1(0,-b),B2(0,b) A1(0,-a),A2(0,a),B1(-b,0),B2(b,0)
轴长 短轴长=2b,长轴长=2a
焦点 (±c,0) (0,±c)
焦距 |F1F2|=2
对称性 对称轴:x轴、y轴 对称中心:原点
离心率 e=∈(0,1)
2.离心率的作用
椭圆离心率e与a,b的关系:e=。因为a>c>0,所以0
【例1】求下列各椭圆的长轴长、短轴长、焦距、顶点坐标、焦点坐标和离心率,并画出它们的草图:(1); (2).
【变式1-1】求适合下列条件的椭圆的标准方程:
(1)长轴长为6,离心率为; (2)经过点,离心率为,焦点在x轴上;
(3)x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
【题型2 椭圆的离心率】
【例2】下列方程表示的椭圆中,形状最接近圆的是( )
A. B. C. D.
【变式2-1】已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若椭圆C的中心到直线AB的距离为|F1F2|,则椭圆C的离心率 .
【变式2-2】设,是椭圆()的左、右焦点,过的直线与交于,两点,若,,则的离心率为( ) A. B. C. D.
【变式2-3】椭圆的左右焦点分别为,点,线段,分别交于两点,过点作的切线交于,且,则的离心率为( )
A. B. C. D.
目标检测
1.椭圆+=1的长轴长为( )A.2 B.4 C.3 D.6
2.如图,直线l:x-2y+2=0过椭圆+=1(a>b>0)的左焦点F1和一个顶点B,该椭圆的离心率为( )A. B. C. D.
3.已知中心在原点的椭圆C的右焦点为F(1,0),离心率等于,则C的方程是( )
A.+=1 B.+=1 C.+=1 D.+y2=1
4.若一个椭圆的长轴长与焦距的和等于短轴长的2倍,则该椭圆的离心率是( )A. B. C. D.
5.若焦点在y轴上的椭圆+=1的离心率为,则m的值为________.
