北京市房山区2024-2025学年高三上学期期中考试数学试题(含解析)
文档属性
| 名称 | 北京市房山区2024-2025学年高三上学期期中考试数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 833.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-23 00:00:00 | ||
图片预览




文档简介
北京市房山区2024-2025学年高三上学期期中考试数学试题
一、单选题
1.已知集合,则( )
A. B. C. D.
2.下列函数值中,在区间上不是单调函数的是( )
A. B. C. D.
3.在平面直角坐标系xOy中,角以Ox为始边,终边与单位圆交于点,则( )
A. B. C. D.
4.已知向量在正方形网格中的位置如图所示.若网格中每个小正方形的边长均为1,则( )
A.4 B. C. D.
5.不等式成立的一个充分不必要条件是( )
A. B. C. D.
6.的零点一定位于以下的区间为( )
A. B. C. D.
7.若且,则与的夹角是( )
A. B. C. D.
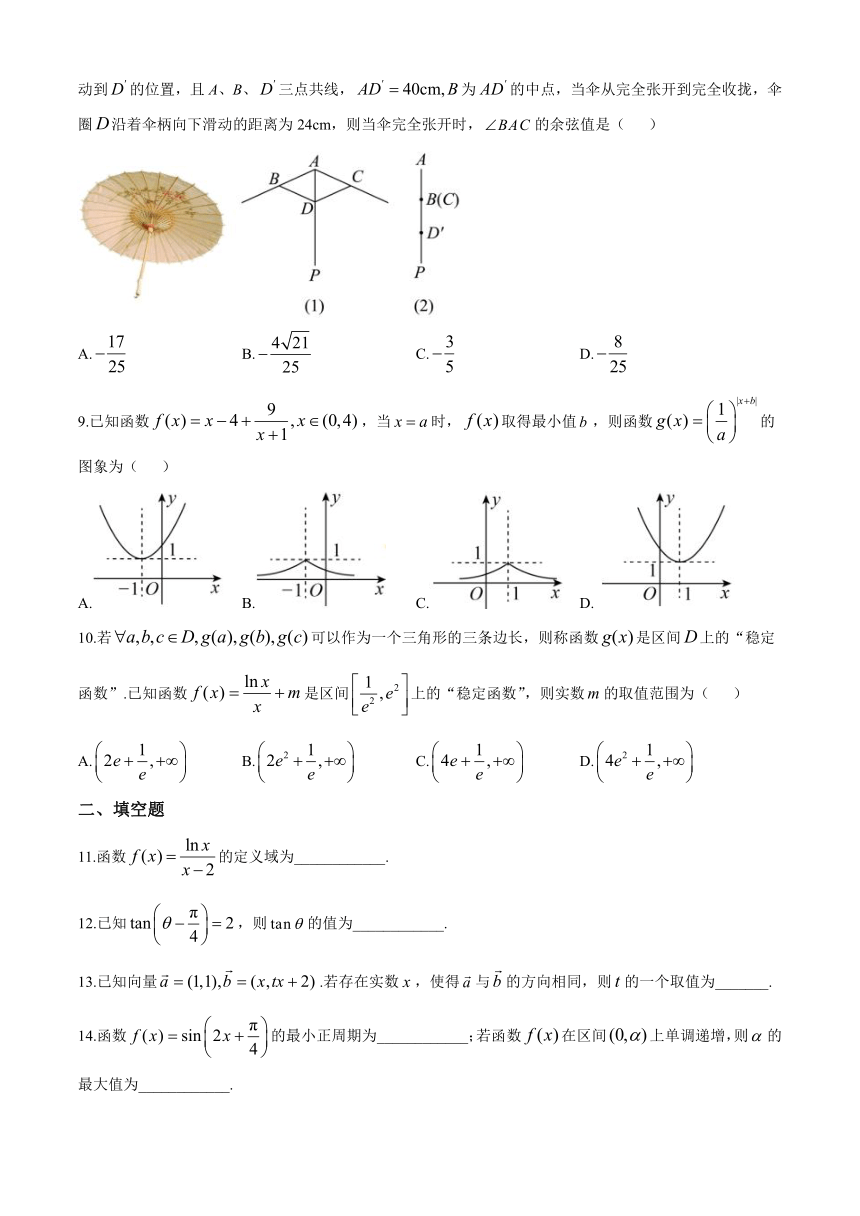
8.我国油纸伞的制作工艺巧妙.如图(1),伞不管是张开还是收拢,伞柄AP始终平分同一平面内两条伞骨所成的角,且,从而保证伞圈能够沿着伞柄滑动.如图(2),伞完全收拢时,伞圈已滑动到的位置,且A、B、三点共线,为的中点,当伞从完全张开到完全收拢,伞圈沿着伞柄向下滑动的距离为24cm,则当伞完全张开时,的余弦值是( )
A. B. C. D.
9.已知函数,当时,取得最小值,则函数的图象为( )
A. B. C. D.
10.若可以作为一个三角形的三条边长,则称函数是区间上的“稳定函数”.已知函数是区间上的“稳定函数”,则实数的取值范围为( )
A. B. C. D.
二、填空题
11.函数的定义域为____________.
12.已知,则的值为____________.
13.已知向量.若存在实数,使得与的方向相同,则的一个取值为_______.
14.函数的最小正周期为____________;若函数在区间上单调递增,则的最大值为____________.
14.已知函数其中且.给出下列四个结论:
①若,则函数的零点是0;
②若函数无最小值,则的取值范围为;
③若,则在区间上单调递减,在区间上单调递增;
④若关于的方程恰有三个不相等的实数根,则的取值范围为,且的取值范围为.
其中,所有正确结论的序号是____________.
三、解答题
16.已知函数.
(1)求的值
(2)求函数在区间上的最小值和最大值.
17.已知四棱锥中,底面ABCD是正方形,是正三角形,平面分别是的中点.
(1)求证:平面ABCD;
(2)求平面EFG与平面ABCD夹角的大小;
18.某商家为了促销,规定每位消费者均可免费参加一次抽奖活动,活动规则如下:在一不透明纸箱中有8张相同的卡片,其中4张卡片上印有“幸”字,另外4张卡片上印有“运”字.消费者从该纸箱中不放回地随机抽取4张卡片,若抽到的4张卡片上都印有同一个字,则获得一张10元代金券;若抽到的4张卡片中恰有3张卡片上印有同一个字,则获得一张5元代金券;若抽到的4张卡片是其他情况,则不获得任何奖励.
(1)求某位消费者在一次抽奖活动中抽到的4张卡片上都印有“幸”字的概率;
(2)记随机变量X为某位消费者在一次抽奖活动中获得代金券的金额数,求X的分布列和数学期望E(X);
(3)该商家规定,消费者若想再次参加该项抽奖活动,则每抽奖一次需支付3元.若你是消费者,是否愿意再次参加该项抽奖活动?请说明理由.
19.在中,.
(1)求;
(2)在下列三个条件中选择一个作为已知,使存在且唯一确定,并求的面积.
条件①:;
条件②:BC边上中线的长为;
条件③:.
注:如果选择多个符合要求的条件分别解答,按第一个解答计分.
20.已知函数.
(1)当时,求的单调区间和极值;
(2)当时,求证:;
21.已知函数.
(I)求证:1是函数的极值点;
(II)设是函数的导函数,求证:.
参考答案
一、单选题
1.【答案】C
【详解】,又则
故选C
2.【答案】D
【详解】由一次函数的性质可知,在区间上单调递增;
由二次函数的性质可知,在区间上单调递增;
由幂函数的性质可知,在区间上单调递增;
结合一次函数的性质可知,在上单调递减,在上单调递增.
故选:D.
3.【答案】C
【详解】依题意得,又因为,所以有.
故选:C.
4.【答案】C
【详解】由图形可知:,
.
故选:C.
5.【答案】A
【详解】不等式,则是成立的一个充分不必要条件.
故选:A
6.【答案】B
【详解】函数在上单调递增,
故函数的零点一定位于区间.
故选:B.
7.【答案】B
【详解】解:设与的夹角是且,
.
.
故选:B.
8.【答案】A
【详解】依题意分析可知,当伞完全张开时,,
因为为的中点,所以,,
当伞完全收拢时,,所以,,
在中,,
所以,.
故选:A.
9.【答案】B
【详解】因,则,于是得,
当且仅当,即时取等号,的最小值为1,则,
函数,其图象关于直线对称,当时,单调递减,只有B选项满足.
故选:B
10.【答案】D
【详解】当时,;当时,;
在上单调递增,在上单调递减,
,
又,
由“稳定函数”定义可知:,即,
解得:,即实数的取值范围为.
故选:D.
二、填空题
11.【答案】
【详解】要使函数有意义,则,解得且,
所以函数的定义域为.
故答案为:.
12.【答案】-3
【详解】因为,所以.
故答案为:-3.
13.【答案】(答案不唯一,小于1的实数均可)
【详解】与方向相同,,
由得:存在实数,使得与方向相同.
故答案为:0(答案不唯一,小于1的实数均可).
14.【答案】
【详解】,故,当时,,故,解得.
故答案为:.
15.【答案】①④
【详解】对于①:当时,显然,当时,无零点;
当时,由可得,所以的零点是0.故(1)正确;
对于②:
当时,简图如下:
当时,简图如下:
当时,简图如下:
当时,简图如下:
由图可知,若无最小值,则或.故②错误;
对于③:由图可知,在区间上单调递减,在区间和上单调递增.故③错误;
对于④:由图可知,只有当且即时,方程才有三个不相等的实数根.
不妨设三个根由小到大依次为,显然.由得,故,且,
所以,故,从而.故④正确.
故答案为:①④.
三、解答题
16【详解】(1)函数
化简可得,
(2),
,所以
即时,即时,取最小值-2;
当时,即时,取最大值1.
17.【详解】(1)因为平面平面ABCD
所以,平面平面ABCD
又是正三角形,O为AD中点
所以
又平面平面平面PAD
所以,平面ABCD
(2)连接OF,因为E、F、G、O分别是PC、PD、BC、AD的中点
所以,所以E、F、G、O四点共面
因为平面PAD,
所以平面PAD
又平面平面PAD
所以平面EFG与平面ABCD夹角的平面角为
又是正三角形,所以
18.【详解】(1)解:记“某位消费者在一次抽奖活动中抽到的4张卡片上都印有‘幸’字”为事件A,则,所以某位消费者在一次抽奖活动中抽到的4张卡片上都印有“幸”字的概率为;
(2)解:依题意随机变量的所有可能取值为0、5、10;
则,
,
,
所以的分布列为:
0 5 10
所以
(3)解:记随机变量为消费者在一次抽奖活动中的收益,则,
所以,
所以我不愿意再次参加该项抽奖活动;
19.【详解】(1)因为,
在中,由正弦定理,可得:,
又因为,所以.
(2)选择条件①;由以及余弦定理得
,该方程无解,故此时三角形不存在,故不能选择条件①
选择条件②
设BC边上的中线为AD,则,
在中,由余弦定理得:
,
因为,所以,
所以的面积为.
选择条件③
方法1:
由题设,因为,所以,
因为,所以
因为,所以,所以,
由余弦定理可得:,
整理得,解得或(舍),
因为,所以,
所以的面积为.
方法2:由题设,因为,所以,
因为,所以
在中,因为,所以,即,所以,
所以,
因为,所以,
所以,
所以,
因为,
所以,
所以的面积为.
方法3:因为且
所以或,
因为,所以,
又因为,
所以即,
所以为等腰三角形,设AC边上的高为BD,则,
由勾股定理,
所以的面积为.
20.【详解】(1)当时,,则,
令,即,
所以当时,单调递增;当时,单调递减;
因此在处取得极大值,,
所以的单调递增区间为,单调递减区间为,在处取得极大值,且极大值为1;
(2)要证,即证,
因此设,则,
令,则,
因为,所以,因此单调递减,且,所以时,;当时,;即时,;当时,;所以在上单调递增,在上单调递减,所以在处取得极大值也是最大值,且,故.
21.【详解】(1)的定义域为
当时,,即;
当时,,即;
根据极值的定义,1是的极值点.
(2)由题意可知,
,
令,
,故在上单调递增.
又,又在上连续,
使得,即,
.(*)
随x的变化情况如下:
— 0 +
极小值
.
由(*)式得,代入上式得
.
令,
,故在上单调递减.
,又.
即.
一、单选题
1.已知集合,则( )
A. B. C. D.
2.下列函数值中,在区间上不是单调函数的是( )
A. B. C. D.
3.在平面直角坐标系xOy中,角以Ox为始边,终边与单位圆交于点,则( )
A. B. C. D.
4.已知向量在正方形网格中的位置如图所示.若网格中每个小正方形的边长均为1,则( )
A.4 B. C. D.
5.不等式成立的一个充分不必要条件是( )
A. B. C. D.
6.的零点一定位于以下的区间为( )
A. B. C. D.
7.若且,则与的夹角是( )
A. B. C. D.
8.我国油纸伞的制作工艺巧妙.如图(1),伞不管是张开还是收拢,伞柄AP始终平分同一平面内两条伞骨所成的角,且,从而保证伞圈能够沿着伞柄滑动.如图(2),伞完全收拢时,伞圈已滑动到的位置,且A、B、三点共线,为的中点,当伞从完全张开到完全收拢,伞圈沿着伞柄向下滑动的距离为24cm,则当伞完全张开时,的余弦值是( )
A. B. C. D.
9.已知函数,当时,取得最小值,则函数的图象为( )
A. B. C. D.
10.若可以作为一个三角形的三条边长,则称函数是区间上的“稳定函数”.已知函数是区间上的“稳定函数”,则实数的取值范围为( )
A. B. C. D.
二、填空题
11.函数的定义域为____________.
12.已知,则的值为____________.
13.已知向量.若存在实数,使得与的方向相同,则的一个取值为_______.
14.函数的最小正周期为____________;若函数在区间上单调递增,则的最大值为____________.
14.已知函数其中且.给出下列四个结论:
①若,则函数的零点是0;
②若函数无最小值,则的取值范围为;
③若,则在区间上单调递减,在区间上单调递增;
④若关于的方程恰有三个不相等的实数根,则的取值范围为,且的取值范围为.
其中,所有正确结论的序号是____________.
三、解答题
16.已知函数.
(1)求的值
(2)求函数在区间上的最小值和最大值.
17.已知四棱锥中,底面ABCD是正方形,是正三角形,平面分别是的中点.
(1)求证:平面ABCD;
(2)求平面EFG与平面ABCD夹角的大小;
18.某商家为了促销,规定每位消费者均可免费参加一次抽奖活动,活动规则如下:在一不透明纸箱中有8张相同的卡片,其中4张卡片上印有“幸”字,另外4张卡片上印有“运”字.消费者从该纸箱中不放回地随机抽取4张卡片,若抽到的4张卡片上都印有同一个字,则获得一张10元代金券;若抽到的4张卡片中恰有3张卡片上印有同一个字,则获得一张5元代金券;若抽到的4张卡片是其他情况,则不获得任何奖励.
(1)求某位消费者在一次抽奖活动中抽到的4张卡片上都印有“幸”字的概率;
(2)记随机变量X为某位消费者在一次抽奖活动中获得代金券的金额数,求X的分布列和数学期望E(X);
(3)该商家规定,消费者若想再次参加该项抽奖活动,则每抽奖一次需支付3元.若你是消费者,是否愿意再次参加该项抽奖活动?请说明理由.
19.在中,.
(1)求;
(2)在下列三个条件中选择一个作为已知,使存在且唯一确定,并求的面积.
条件①:;
条件②:BC边上中线的长为;
条件③:.
注:如果选择多个符合要求的条件分别解答,按第一个解答计分.
20.已知函数.
(1)当时,求的单调区间和极值;
(2)当时,求证:;
21.已知函数.
(I)求证:1是函数的极值点;
(II)设是函数的导函数,求证:.
参考答案
一、单选题
1.【答案】C
【详解】,又则
故选C
2.【答案】D
【详解】由一次函数的性质可知,在区间上单调递增;
由二次函数的性质可知,在区间上单调递增;
由幂函数的性质可知,在区间上单调递增;
结合一次函数的性质可知,在上单调递减,在上单调递增.
故选:D.
3.【答案】C
【详解】依题意得,又因为,所以有.
故选:C.
4.【答案】C
【详解】由图形可知:,
.
故选:C.
5.【答案】A
【详解】不等式,则是成立的一个充分不必要条件.
故选:A
6.【答案】B
【详解】函数在上单调递增,
故函数的零点一定位于区间.
故选:B.
7.【答案】B
【详解】解:设与的夹角是且,
.
.
故选:B.
8.【答案】A
【详解】依题意分析可知,当伞完全张开时,,
因为为的中点,所以,,
当伞完全收拢时,,所以,,
在中,,
所以,.
故选:A.
9.【答案】B
【详解】因,则,于是得,
当且仅当,即时取等号,的最小值为1,则,
函数,其图象关于直线对称,当时,单调递减,只有B选项满足.
故选:B
10.【答案】D
【详解】当时,;当时,;
在上单调递增,在上单调递减,
,
又,
由“稳定函数”定义可知:,即,
解得:,即实数的取值范围为.
故选:D.
二、填空题
11.【答案】
【详解】要使函数有意义,则,解得且,
所以函数的定义域为.
故答案为:.
12.【答案】-3
【详解】因为,所以.
故答案为:-3.
13.【答案】(答案不唯一,小于1的实数均可)
【详解】与方向相同,,
由得:存在实数,使得与方向相同.
故答案为:0(答案不唯一,小于1的实数均可).
14.【答案】
【详解】,故,当时,,故,解得.
故答案为:.
15.【答案】①④
【详解】对于①:当时,显然,当时,无零点;
当时,由可得,所以的零点是0.故(1)正确;
对于②:
当时,简图如下:
当时,简图如下:
当时,简图如下:
当时,简图如下:
由图可知,若无最小值,则或.故②错误;
对于③:由图可知,在区间上单调递减,在区间和上单调递增.故③错误;
对于④:由图可知,只有当且即时,方程才有三个不相等的实数根.
不妨设三个根由小到大依次为,显然.由得,故,且,
所以,故,从而.故④正确.
故答案为:①④.
三、解答题
16【详解】(1)函数
化简可得,
(2),
,所以
即时,即时,取最小值-2;
当时,即时,取最大值1.
17.【详解】(1)因为平面平面ABCD
所以,平面平面ABCD
又是正三角形,O为AD中点
所以
又平面平面平面PAD
所以,平面ABCD
(2)连接OF,因为E、F、G、O分别是PC、PD、BC、AD的中点
所以,所以E、F、G、O四点共面
因为平面PAD,
所以平面PAD
又平面平面PAD
所以平面EFG与平面ABCD夹角的平面角为
又是正三角形,所以
18.【详解】(1)解:记“某位消费者在一次抽奖活动中抽到的4张卡片上都印有‘幸’字”为事件A,则,所以某位消费者在一次抽奖活动中抽到的4张卡片上都印有“幸”字的概率为;
(2)解:依题意随机变量的所有可能取值为0、5、10;
则,
,
,
所以的分布列为:
0 5 10
所以
(3)解:记随机变量为消费者在一次抽奖活动中的收益,则,
所以,
所以我不愿意再次参加该项抽奖活动;
19.【详解】(1)因为,
在中,由正弦定理,可得:,
又因为,所以.
(2)选择条件①;由以及余弦定理得
,该方程无解,故此时三角形不存在,故不能选择条件①
选择条件②
设BC边上的中线为AD,则,
在中,由余弦定理得:
,
因为,所以,
所以的面积为.
选择条件③
方法1:
由题设,因为,所以,
因为,所以
因为,所以,所以,
由余弦定理可得:,
整理得,解得或(舍),
因为,所以,
所以的面积为.
方法2:由题设,因为,所以,
因为,所以
在中,因为,所以,即,所以,
所以,
因为,所以,
所以,
所以,
因为,
所以,
所以的面积为.
方法3:因为且
所以或,
因为,所以,
又因为,
所以即,
所以为等腰三角形,设AC边上的高为BD,则,
由勾股定理,
所以的面积为.
20.【详解】(1)当时,,则,
令,即,
所以当时,单调递增;当时,单调递减;
因此在处取得极大值,,
所以的单调递增区间为,单调递减区间为,在处取得极大值,且极大值为1;
(2)要证,即证,
因此设,则,
令,则,
因为,所以,因此单调递减,且,所以时,;当时,;即时,;当时,;所以在上单调递增,在上单调递减,所以在处取得极大值也是最大值,且,故.
21.【详解】(1)的定义域为
当时,,即;
当时,,即;
根据极值的定义,1是的极值点.
(2)由题意可知,
,
令,
,故在上单调递增.
又,又在上连续,
使得,即,
.(*)
随x的变化情况如下:
— 0 +
极小值
.
由(*)式得,代入上式得
.
令,
,故在上单调递减.
,又.
即.
同课章节目录
