2024-2025学年苏科版数学八年级上册综合训练(第一章~第六章)(含答案)
文档属性
| 名称 | 2024-2025学年苏科版数学八年级上册综合训练(第一章~第六章)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 623.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 22:07:24 | ||
图片预览


文档简介
2024-2025学年苏科版数学八年级上册综合训练(第一章~第六章)
一、单选题
1.在下列四所大学的校标中,内圆部分的图案不是轴对称图形的是( )
A. B.
C. D.
2.下列数组中,能构成勾股数的是( )
A.1,1, B.0.3,0.4,0.5 C.5,12,13 D.,,
3.一组数:,其中无理数有( )
A.1个 B.2个 C.3个 D.4个
4.函数中,随的增大而增大,则直线经过( )
A.第一、三、四象限 B.第二、三、四象限
C.第一、二、四象限 D.第一、二、三象限
5.如图在和中,点在同一直线上,若,则的大小为( )
A. B. C. D.
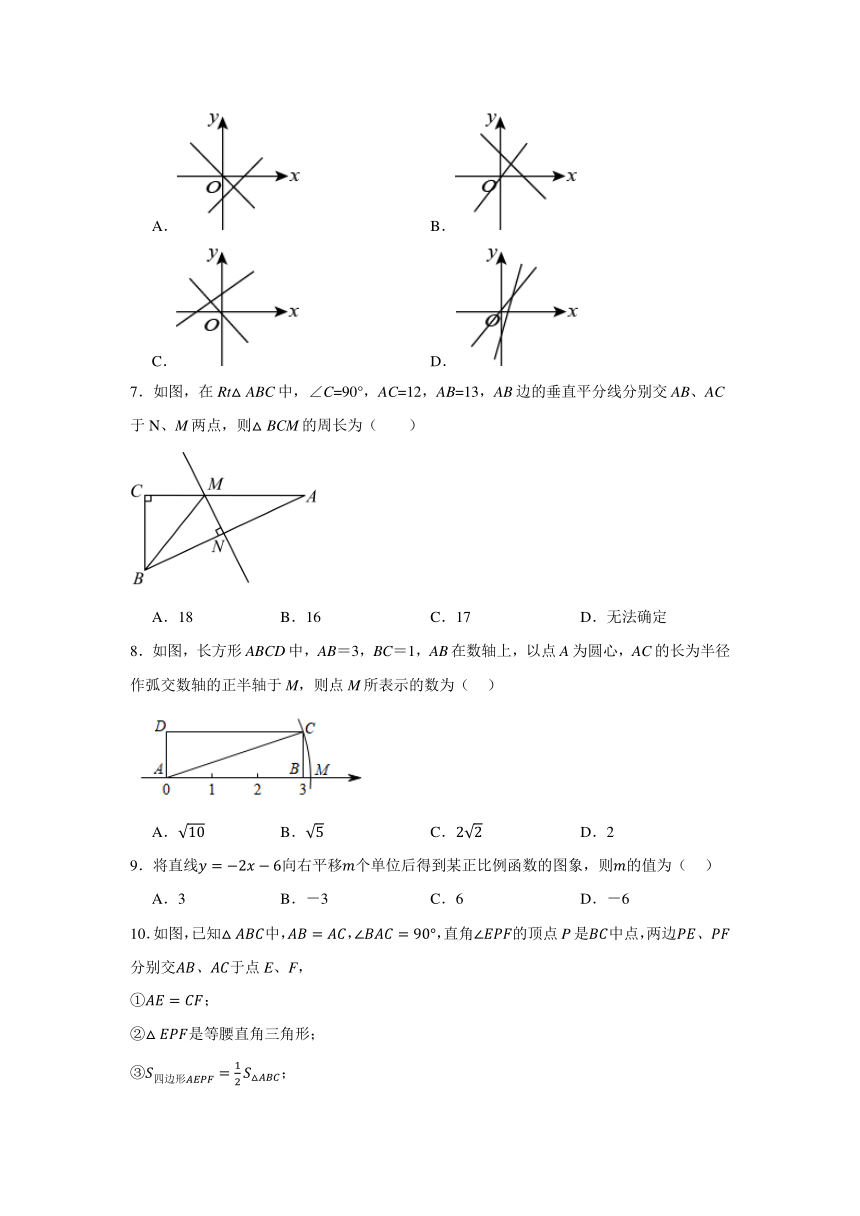
6.下图中,能表示一次函数与正比例函数(m,n为常数,且)的大致图象的是( )
A. B.
C. D.
7.如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
A.18 B.16 C.17 D.无法确定
8.如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为( )
A. B. C. D.2
9.将直线向右平移个单位后得到某正比例函数的图象,则的值为( )
A.3 B.-3 C.6 D.-6
10.如图,已知中,,,直角的顶点P是中点,两边分别交于点E、F,
①;
②是等腰直角三角形;
③;
④当在内绕顶点P旋转时(点E不与A、B重合),.
上述结论中始终正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题
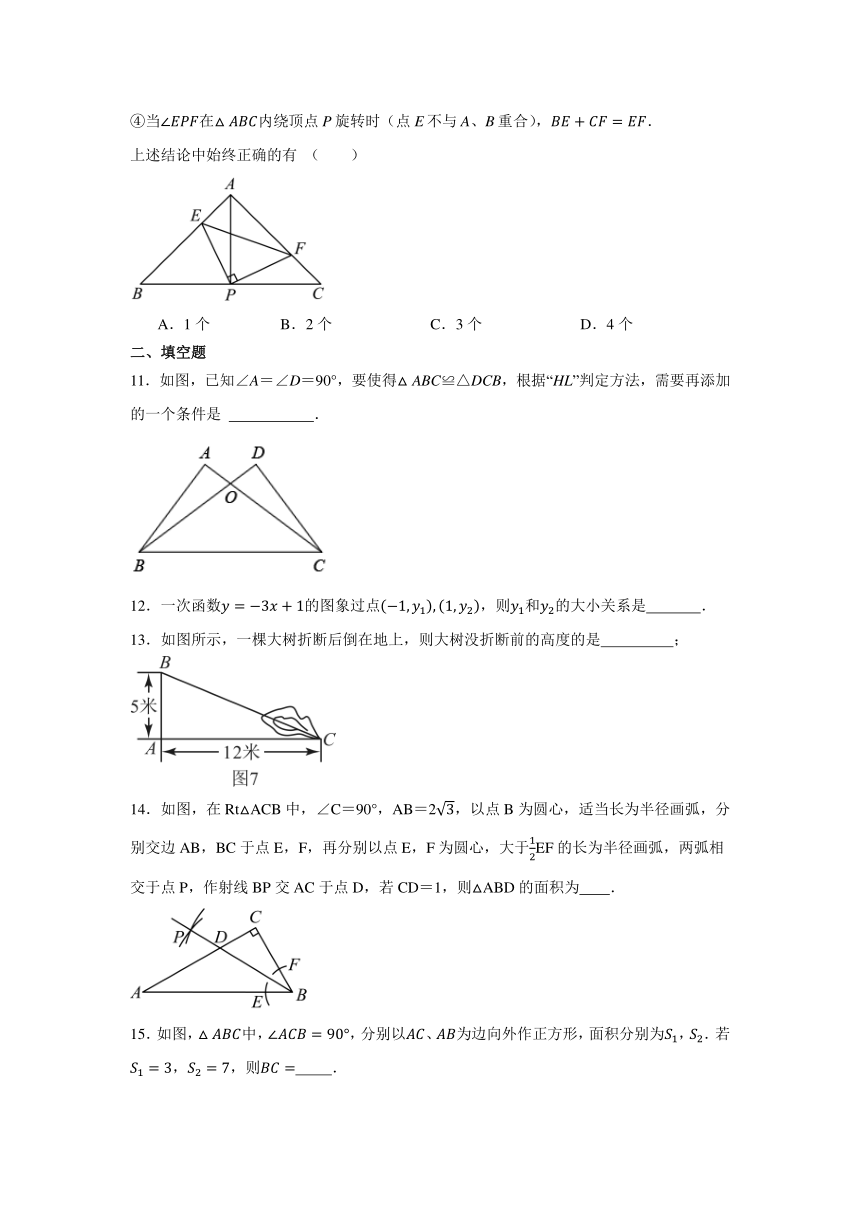
11.如图,已知∠A=∠D=90°,要使得△ABC≌△DCB,根据“HL”判定方法,需要再添加的一个条件是 .
12.一次函数的图象过点,则和的大小关系是 .
13.如图所示,一棵大树折断后倒在地上,则大树没折断前的高度的是 ;
14.如图,在RtACB中,∠C=90°,AB=2,以点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点P,作射线BP交AC于点D,若CD=1,则ABD的面积为 .
15.如图,中,,分别以、为边向外作正方形,面积分别为,.若,,则 .
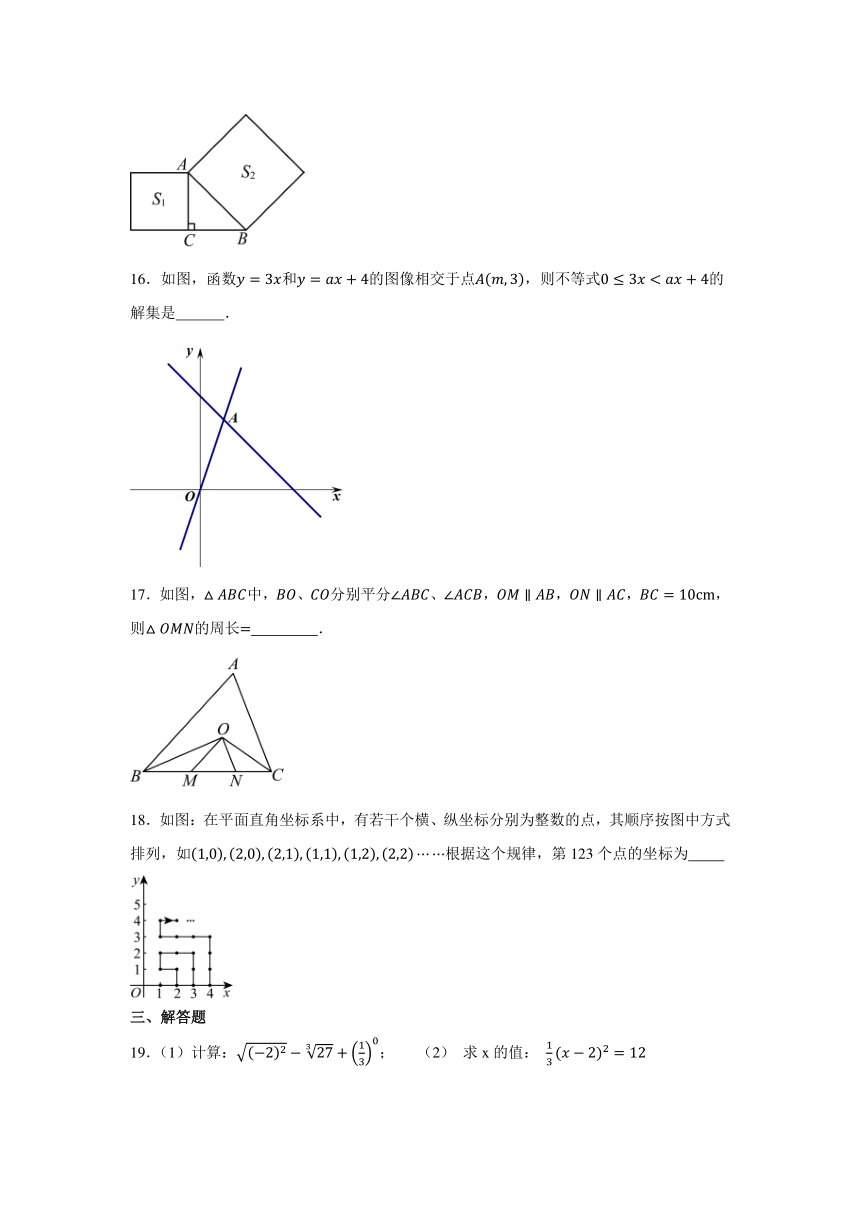
16.如图,函数和的图像相交于点,则不等式的解集是 .
17.如图,中,、分别平分、,,,,则的周长 .
18.如图:在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中方式排列,如根据这个规律,第123个点的坐标为
三、解答题
19.(1)计算:; (2) 求x的值:
20.已知:如图,点E、F在上,与交于点G, .求证:.
21.当蜡烛被点燃后,蜡烛的长度会随燃烧时间发生变化.研究表明,在蜡烛可燃烧长度内,蜡烛剩余的长度y()与燃烧时间x()之间为一次函数关系,某实验小组将得到的数据绘制成如下表格.
燃烧时间x() 0 1 2 3
剩余长度y() 20 17 14 11
(1)求蜡烛剩余长度y()与燃烧时间x()之间的函数表达式,并写出自变量的取值范围;
(2)当蜡烛燃烧5后,求蜡烛剩余的长度.
22.如图,一架2.5m长的梯子斜靠在墙上,此时梯足B距底端O为0.7m.
(1)求的长度.
(2)如果梯子下滑0.4m,则梯子滑出的距离是否等于0.4m?请通过计算来说明理由.
23.小明和小强两同学分别从甲地出发,沿同一条道路骑自行车到乙地参加社会实践活动,小明同学先从甲地出发,1小时后小强出发,小明则放慢速度继续前行,小明和小强距甲地的距离y(千米)与小明出发的时间x(小时)之间的函数图象如图所示.
(1)小强同学骑自行车的速度为___________千米/小时;
(2)求小明距甲地的距离y与x之间的函数关系式;
(3)当小强到达乙地时,求小明距乙地的距离.
24.已知为等边三角形.
(1)如图1,点D为边上一点,以为边作等边三角形,连接,求证:.
(2)如图2,以为腰作等腰直角三角形,取斜边的中点E,连接,交于点F.求证:.
(3)如图3,若,点P是边上一定点且,若点D为射线上一动点,以为边向右侧作等边,连接、,直接写出的最小值.
25.随着人们生活条件的不断改善,对饮用水的要求越来越高,更加关注品质和健康,国内饮用水市场迎来高端时代某经销商从市场得知如下信息:
甲种品牌净水器 乙种品牌净水器
进价(元/台) 1800 1500
售价(元/台) 3000 2500
该经销商计划用8.04万元一次性购进这两种品牌净水器共50台,设该经销商购进甲种品牌净水器x台,这50台净水器全部销售完后获得的利润为y元.
(1)求y与x之间的函数关系式,并求出自变量x的取值范围;
(2)若要求全部销售完后获得的利润不少于5.3万元,则该经销商有几种进货方案?
(3)在(2)的条件下,选择哪种进货方案,该经销商获利最大?最大利润是多少元?
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B B A A C A A C
11.AB=DC或AC=BD
12.
13.米
14.
15.2
16.0≤x<1
17.
18.
19.(1)原式=2 3+1=0;
(2)(x-2)2=12;
(x-2)2=36;
x-2=±6,
x=2±6,
x1=8,x2=-4.
20.证明:∵
∴为等腰三角形,
∴
∵在和中,
∴
在和中,
,
∴,
∴
又∵
∴
即.
21.(1)解:观察表中数据可得蜡烛初始长度为20,每燃烧1蜡烛减少3,
函数表达式为.
当蜡烛燃烧完,即时,,
自变量的取值范围为.
(2)解:当时,.
答:当蜡烛燃烧5后,蜡烛剩余长度为5.
22.(1)解:由题意,得:,
由勾股定理,得:;
(2)不等于,理由如下:
由题意,得:,
∴,
在中,由勾股定理,得:,
∴;
23.(1)由图象可知,小强同学在小时内骑了千米,
故其骑自行车的速度为(千米/小时),
(2)设小明距离甲地的距离与之间的函数关系式为(、为常数,且),
当时,点和在直线上,代入到中,
可得,解得,
即:当时,小明距离甲地的距离与之间的函数关系式为
点和在直线上,代入到中,
可得,解得,
∴当时,小明距离甲地的距离与之间的函数关系式为 .
综上所述:小明距离甲地的距离与之间的函数关系式为.
(3)设小强距离甲地的距离与之间的函数关系式为(、为常数,且),
小强同学骑自行车的速度为千米/小时,且点、在直线上,
∴,解得,
故小强距离甲地的距离与之间的函数关系式为:,
当小强到达乙地时,,代入解得:,解得:,
将代入到中,得:,
故(千米),
∴当小强到达乙地时,小明距乙地的距离为千米.
24.(1)证明:∵等边和等边;
∴,;
∵;
∴;
∴
(2)∵;
∴;
∵,;
∴;
∴;
即;
∵三角形是等腰直角三角形,E为中点
∴平分;
∴;
∴;
上取一点H,使;
∴是等边三角形;
∴;
即;
∵,
,
;
∴;
∴;
即.
(3)的最小值为.
25.解:(1)根据题意得:y=(3000﹣1800)x+(2500﹣1500)(50﹣x)=200x+50000.
根据题意,,解得,x≤18.
自变量取值范围是:x≤18.
(2)根据全部销售完后获得的利润不少于5.3万元得:,
解得:x≥15,
由(1)得,15≤x≤18.
∵x为整数,
∴x=15,16,17,18,
∴该经销商有四种进货方案:方案①购进甲品牌15台、购进乙品牌35台;方案②购进甲品牌16台、购进乙品牌34台;方案③购进甲品牌17台、购进乙品牌33台;方案④购进甲品牌18台、购进乙品牌32台.
(3)由(1)(2)得,y=200x+50000(15≤x≤18).
∵k=200>0,
∴y随x值的增大而增大,
∴当x=18时,y取最大值,最大值为53600元.
选择方案④购进甲品牌18台、购进乙品牌32台利润最大,最大值为53600元.
一、单选题
1.在下列四所大学的校标中,内圆部分的图案不是轴对称图形的是( )
A. B.
C. D.
2.下列数组中,能构成勾股数的是( )
A.1,1, B.0.3,0.4,0.5 C.5,12,13 D.,,
3.一组数:,其中无理数有( )
A.1个 B.2个 C.3个 D.4个
4.函数中,随的增大而增大,则直线经过( )
A.第一、三、四象限 B.第二、三、四象限
C.第一、二、四象限 D.第一、二、三象限
5.如图在和中,点在同一直线上,若,则的大小为( )
A. B. C. D.
6.下图中,能表示一次函数与正比例函数(m,n为常数,且)的大致图象的是( )
A. B.
C. D.
7.如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
A.18 B.16 C.17 D.无法确定
8.如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为( )
A. B. C. D.2
9.将直线向右平移个单位后得到某正比例函数的图象,则的值为( )
A.3 B.-3 C.6 D.-6
10.如图,已知中,,,直角的顶点P是中点,两边分别交于点E、F,
①;
②是等腰直角三角形;
③;
④当在内绕顶点P旋转时(点E不与A、B重合),.
上述结论中始终正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,已知∠A=∠D=90°,要使得△ABC≌△DCB,根据“HL”判定方法,需要再添加的一个条件是 .
12.一次函数的图象过点,则和的大小关系是 .
13.如图所示,一棵大树折断后倒在地上,则大树没折断前的高度的是 ;
14.如图,在RtACB中,∠C=90°,AB=2,以点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点P,作射线BP交AC于点D,若CD=1,则ABD的面积为 .
15.如图,中,,分别以、为边向外作正方形,面积分别为,.若,,则 .
16.如图,函数和的图像相交于点,则不等式的解集是 .
17.如图,中,、分别平分、,,,,则的周长 .
18.如图:在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中方式排列,如根据这个规律,第123个点的坐标为
三、解答题
19.(1)计算:; (2) 求x的值:
20.已知:如图,点E、F在上,与交于点G, .求证:.
21.当蜡烛被点燃后,蜡烛的长度会随燃烧时间发生变化.研究表明,在蜡烛可燃烧长度内,蜡烛剩余的长度y()与燃烧时间x()之间为一次函数关系,某实验小组将得到的数据绘制成如下表格.
燃烧时间x() 0 1 2 3
剩余长度y() 20 17 14 11
(1)求蜡烛剩余长度y()与燃烧时间x()之间的函数表达式,并写出自变量的取值范围;
(2)当蜡烛燃烧5后,求蜡烛剩余的长度.
22.如图,一架2.5m长的梯子斜靠在墙上,此时梯足B距底端O为0.7m.
(1)求的长度.
(2)如果梯子下滑0.4m,则梯子滑出的距离是否等于0.4m?请通过计算来说明理由.
23.小明和小强两同学分别从甲地出发,沿同一条道路骑自行车到乙地参加社会实践活动,小明同学先从甲地出发,1小时后小强出发,小明则放慢速度继续前行,小明和小强距甲地的距离y(千米)与小明出发的时间x(小时)之间的函数图象如图所示.
(1)小强同学骑自行车的速度为___________千米/小时;
(2)求小明距甲地的距离y与x之间的函数关系式;
(3)当小强到达乙地时,求小明距乙地的距离.
24.已知为等边三角形.
(1)如图1,点D为边上一点,以为边作等边三角形,连接,求证:.
(2)如图2,以为腰作等腰直角三角形,取斜边的中点E,连接,交于点F.求证:.
(3)如图3,若,点P是边上一定点且,若点D为射线上一动点,以为边向右侧作等边,连接、,直接写出的最小值.
25.随着人们生活条件的不断改善,对饮用水的要求越来越高,更加关注品质和健康,国内饮用水市场迎来高端时代某经销商从市场得知如下信息:
甲种品牌净水器 乙种品牌净水器
进价(元/台) 1800 1500
售价(元/台) 3000 2500
该经销商计划用8.04万元一次性购进这两种品牌净水器共50台,设该经销商购进甲种品牌净水器x台,这50台净水器全部销售完后获得的利润为y元.
(1)求y与x之间的函数关系式,并求出自变量x的取值范围;
(2)若要求全部销售完后获得的利润不少于5.3万元,则该经销商有几种进货方案?
(3)在(2)的条件下,选择哪种进货方案,该经销商获利最大?最大利润是多少元?
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B B A A C A A C
11.AB=DC或AC=BD
12.
13.米
14.
15.2
16.0≤x<1
17.
18.
19.(1)原式=2 3+1=0;
(2)(x-2)2=12;
(x-2)2=36;
x-2=±6,
x=2±6,
x1=8,x2=-4.
20.证明:∵
∴为等腰三角形,
∴
∵在和中,
∴
在和中,
,
∴,
∴
又∵
∴
即.
21.(1)解:观察表中数据可得蜡烛初始长度为20,每燃烧1蜡烛减少3,
函数表达式为.
当蜡烛燃烧完,即时,,
自变量的取值范围为.
(2)解:当时,.
答:当蜡烛燃烧5后,蜡烛剩余长度为5.
22.(1)解:由题意,得:,
由勾股定理,得:;
(2)不等于,理由如下:
由题意,得:,
∴,
在中,由勾股定理,得:,
∴;
23.(1)由图象可知,小强同学在小时内骑了千米,
故其骑自行车的速度为(千米/小时),
(2)设小明距离甲地的距离与之间的函数关系式为(、为常数,且),
当时,点和在直线上,代入到中,
可得,解得,
即:当时,小明距离甲地的距离与之间的函数关系式为
点和在直线上,代入到中,
可得,解得,
∴当时,小明距离甲地的距离与之间的函数关系式为 .
综上所述:小明距离甲地的距离与之间的函数关系式为.
(3)设小强距离甲地的距离与之间的函数关系式为(、为常数,且),
小强同学骑自行车的速度为千米/小时,且点、在直线上,
∴,解得,
故小强距离甲地的距离与之间的函数关系式为:,
当小强到达乙地时,,代入解得:,解得:,
将代入到中,得:,
故(千米),
∴当小强到达乙地时,小明距乙地的距离为千米.
24.(1)证明:∵等边和等边;
∴,;
∵;
∴;
∴
(2)∵;
∴;
∵,;
∴;
∴;
即;
∵三角形是等腰直角三角形,E为中点
∴平分;
∴;
∴;
上取一点H,使;
∴是等边三角形;
∴;
即;
∵,
,
;
∴;
∴;
即.
(3)的最小值为.
25.解:(1)根据题意得:y=(3000﹣1800)x+(2500﹣1500)(50﹣x)=200x+50000.
根据题意,,解得,x≤18.
自变量取值范围是:x≤18.
(2)根据全部销售完后获得的利润不少于5.3万元得:,
解得:x≥15,
由(1)得,15≤x≤18.
∵x为整数,
∴x=15,16,17,18,
∴该经销商有四种进货方案:方案①购进甲品牌15台、购进乙品牌35台;方案②购进甲品牌16台、购进乙品牌34台;方案③购进甲品牌17台、购进乙品牌33台;方案④购进甲品牌18台、购进乙品牌32台.
(3)由(1)(2)得,y=200x+50000(15≤x≤18).
∵k=200>0,
∴y随x值的增大而增大,
∴当x=18时,y取最大值,最大值为53600元.
选择方案④购进甲品牌18台、购进乙品牌32台利润最大,最大值为53600元.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
