3.1.2 空间两点间的距离公式(15页)课件 2024-2025学年高二数学北师版(2019)选择性必修1
文档属性
| 名称 | 3.1.2 空间两点间的距离公式(15页)课件 2024-2025学年高二数学北师版(2019)选择性必修1 |

|
|
| 格式 | pptx | ||
| 文件大小 | 366.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-23 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
3.1.2 空间两点间的距离公式
1.了解推导空间两点间的距离公式的过程.
2.会用空间两点间的距离公式求空间中两点间的距离.
思考:在空间直角坐标系中,两点间的距离与两点的坐标有何关系
在空间直角坐标系中,给定P(x1,y1,z1),Q(x2,y2,z2)两点.
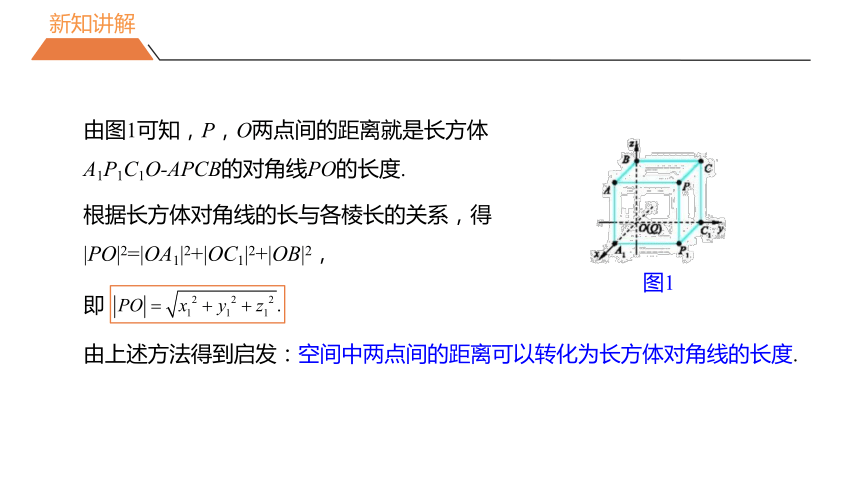
特殊情况:若其中一点为原点,不妨设点Q为原点O,过点P分别作与三条坐标轴垂直的平面,则被各坐标平面所截可得长方体A1P1C1O-APCB(如图1),且长方体的棱长满足|OA1|=|x1|,|OC1|=|y1|,|OB|=|z1|.
图1
由图1可知,P,O两点间的距离就是长方体A1P1C1O-APCB的对角线PO的长度.
根据长方体对角线的长与各棱长的关系,得|PO|2=|OA1|2+|OC1|2+|OB|2,
即
由上述方法得到启发:空间中两点间的距离可以转化为长方体对角线的长度.
图1
一般情况:对于空间任意P,Q两点,过点P分别作与三条坐标轴垂直的平面,过点Q也分别作与三条坐标轴垂直的平面(如图2),
当这六个平面均不重合时,它们围成一个长方体PCBA-EFQD,且长方体的各棱所在的直线均与某条坐标轴平行或重合.
由图易知,C,B两点的坐标分别为(x1,y2,z1),(x2,y2,z1),
∵CB平行于x轴,∴|CB|=|x2-x1|.
同理有|PC|=|y2-y1|,|BQ|=|z2-z1|.
图2
图2
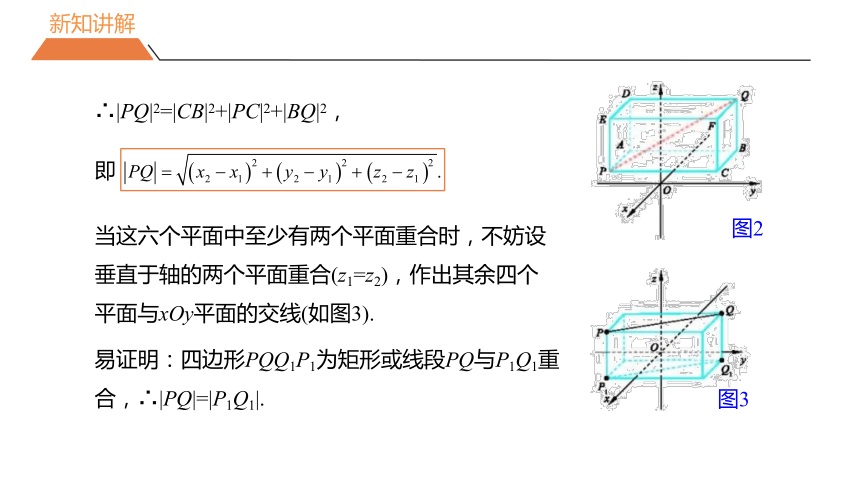
∴|PQ|2=|CB|2+|PC|2+|BQ|2,
即
当这六个平面中至少有两个平面重合时,不妨设垂直于轴的两个平面重合(z1=z2),作出其余四个平面与xOy平面的交线(如图3).
易证明:四边形PQQ1P1为矩形或线段PQ与P1Q1重合,∴|PQ|=|P1Q1|.
图3
图3
由图3易知,P1,Q1两点的坐标分别为(x1,y1,0),(x2,y2,0),
再根据平面上两点间的距离公式,有
于是仍有
归纳总结
已知空间中P(x1,y1,z1),Q(x2,y2,z2)两点,则P,Q两点间的距离为
这就是空间两点间的距离公式.
例1:已知△ABC的三个顶点A(1,5,2),B(2,3,4),C(3,1,5).
(1)求△ABC中最短边的边长;
(2)求AC边上中线的长度.
解:(1)由空间两点间距离公式得
|AB|==3,
|BC|==,
|AC|==,
∴△ABC中最短边是|BC|,其长度为.
例1:已知△ABC的三个顶点A(1,5,2),B(2,3,4),C(3,1,5).
(1)求△ABC中最短边的边长;
(2)求AC边上中线的长度.
(2)由中点坐标公式得,AC的中点坐标为(2,3,),
∴AC边上中线的长度为=.
1.求空间两点间的距离问题就是把点的坐标代入距离公式进行计算,其中确定点的坐标或合理设出点的坐标是关键.
2.若所给题目中未建立坐标系,需结合已知条件建立适当的坐标系,再利用空间两点间的距离公式计算.
归纳总结
例2:设点P在x轴上,它到P1(0,,3)的距离是到点P2(0,1,-1)的距离的2倍,求点P的坐标.
解:∵P在x轴上,∴设P点坐标为(x,0,0),
又∵|PP1|=2|PP2|,
∴,
∴x=±1,
∴点P坐标为(1,0,0)或(-1,0,0).
由空间两点间距离求点的坐标的方法:
归纳总结
(1)若已知点到定点的距离以及点在特殊位置,则可直接设出该点坐标,利用待定系数法求解点的坐标.
(2)若已知一点到两个定点的距离之间的关系,以及其他的一些条件,则可以列出关于点的坐标的方程进行求解.
1.在空间直角坐标系中,设A(1,2,a),B(2,3,4),若|AB|=,则实数a的值是( )
A.3或5 B.-3或-5
C.3或-5 D.-3或5
2.已知点A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
3.如果点P在z轴上,且满足|PO|=1(O是坐标原点),则点P到点A(1,1,1)的距离是 .
A
B
或
空间两点间距离公式是什么?回顾其推导过程.
3.1.2 空间两点间的距离公式
1.了解推导空间两点间的距离公式的过程.
2.会用空间两点间的距离公式求空间中两点间的距离.
思考:在空间直角坐标系中,两点间的距离与两点的坐标有何关系
在空间直角坐标系中,给定P(x1,y1,z1),Q(x2,y2,z2)两点.
特殊情况:若其中一点为原点,不妨设点Q为原点O,过点P分别作与三条坐标轴垂直的平面,则被各坐标平面所截可得长方体A1P1C1O-APCB(如图1),且长方体的棱长满足|OA1|=|x1|,|OC1|=|y1|,|OB|=|z1|.
图1
由图1可知,P,O两点间的距离就是长方体A1P1C1O-APCB的对角线PO的长度.
根据长方体对角线的长与各棱长的关系,得|PO|2=|OA1|2+|OC1|2+|OB|2,
即
由上述方法得到启发:空间中两点间的距离可以转化为长方体对角线的长度.
图1
一般情况:对于空间任意P,Q两点,过点P分别作与三条坐标轴垂直的平面,过点Q也分别作与三条坐标轴垂直的平面(如图2),
当这六个平面均不重合时,它们围成一个长方体PCBA-EFQD,且长方体的各棱所在的直线均与某条坐标轴平行或重合.
由图易知,C,B两点的坐标分别为(x1,y2,z1),(x2,y2,z1),
∵CB平行于x轴,∴|CB|=|x2-x1|.
同理有|PC|=|y2-y1|,|BQ|=|z2-z1|.
图2
图2
∴|PQ|2=|CB|2+|PC|2+|BQ|2,
即
当这六个平面中至少有两个平面重合时,不妨设垂直于轴的两个平面重合(z1=z2),作出其余四个平面与xOy平面的交线(如图3).
易证明:四边形PQQ1P1为矩形或线段PQ与P1Q1重合,∴|PQ|=|P1Q1|.
图3
图3
由图3易知,P1,Q1两点的坐标分别为(x1,y1,0),(x2,y2,0),
再根据平面上两点间的距离公式,有
于是仍有
归纳总结
已知空间中P(x1,y1,z1),Q(x2,y2,z2)两点,则P,Q两点间的距离为
这就是空间两点间的距离公式.
例1:已知△ABC的三个顶点A(1,5,2),B(2,3,4),C(3,1,5).
(1)求△ABC中最短边的边长;
(2)求AC边上中线的长度.
解:(1)由空间两点间距离公式得
|AB|==3,
|BC|==,
|AC|==,
∴△ABC中最短边是|BC|,其长度为.
例1:已知△ABC的三个顶点A(1,5,2),B(2,3,4),C(3,1,5).
(1)求△ABC中最短边的边长;
(2)求AC边上中线的长度.
(2)由中点坐标公式得,AC的中点坐标为(2,3,),
∴AC边上中线的长度为=.
1.求空间两点间的距离问题就是把点的坐标代入距离公式进行计算,其中确定点的坐标或合理设出点的坐标是关键.
2.若所给题目中未建立坐标系,需结合已知条件建立适当的坐标系,再利用空间两点间的距离公式计算.
归纳总结
例2:设点P在x轴上,它到P1(0,,3)的距离是到点P2(0,1,-1)的距离的2倍,求点P的坐标.
解:∵P在x轴上,∴设P点坐标为(x,0,0),
又∵|PP1|=2|PP2|,
∴,
∴x=±1,
∴点P坐标为(1,0,0)或(-1,0,0).
由空间两点间距离求点的坐标的方法:
归纳总结
(1)若已知点到定点的距离以及点在特殊位置,则可直接设出该点坐标,利用待定系数法求解点的坐标.
(2)若已知一点到两个定点的距离之间的关系,以及其他的一些条件,则可以列出关于点的坐标的方程进行求解.
1.在空间直角坐标系中,设A(1,2,a),B(2,3,4),若|AB|=,则实数a的值是( )
A.3或5 B.-3或-5
C.3或-5 D.-3或5
2.已知点A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
3.如果点P在z轴上,且满足|PO|=1(O是坐标原点),则点P到点A(1,1,1)的距离是 .
A
B
或
空间两点间距离公式是什么?回顾其推导过程.
同课章节目录
