第9章 多边形 单元检测(解析版)
文档属性
| 名称 | 第9章 多边形 单元检测(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-23 13:30:07 | ||
图片预览



文档简介
第9章 多边形 单元检测
(45分钟 100分)
一、选择题(每小题4分,共28分)
1.不一定在三角形内部的线段是 ( )
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.以上都不对
【解析】选C.锐角三角形的三条高在三角形内部,直角三角形的两条直角边也是三角形的高,钝角三角形有两条高在三角形外部.
2.已知△ABC的一个外角为50°,则△ABC一定是 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.锐角三角形或钝角三角形
【解析】选B.一个外角为50°,所以与它相邻的内角的度数为130°,所以三角形为钝角三角形.
【方法技巧】已知三角形的外角判断三角形的形状
1.三角形的外角有一个锐角,则此三角形一定是钝角三角形.
2.三角形的外角有一个直角,则此三角形一定是直角三角形.
3.三角形的外角都是钝角,则此三角形一定是锐角三角形.
3.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是 ( )
A.5 B.6 C.11 D.16
【解析】选C.因为已知三角形两边的长分别是4和10,所以第三边x的范围是6【变式训练】已知三角形两边的长分别是2和6,且第三边的长为偶数,则此三角形第三边的长是 .
【解析】因为已知三角形两边的长分别是2和6,
所以第三边x的范围是4在这个范围内,只有6为偶数,
所以第三边的长为6.
答案:6
4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的
是 ( )
【解析】选A.根据三角形高的定义进行判断.
5.已知等腰三角形三边中有两边的长分别为4,9,则这个等腰三角形的周长
为 ( )
A.13 B.17
C.22 D.17或22
【解析】选C.当4为底时,其他两边都为9,
∵9,9,4可以构成三角形,
∴三角形的周长为22;
当4为腰时,其他两边为9和4,
∵4+4=8<9,∴不能构成三角形,故舍去.
6.如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数
是 ( )
A.75° B.55° C.40° D.35°
【解析】选C.两直线平行,同位角相等,三角形的一个外角等于与它不相邻的两个内角之和,所以75°=∠2+∠3,所以∠3=40°.
7.如图,△ABC中,D是△ABC的重心,连结AD并延长交BC于点E,若BC=6,则EC= ( )
A.2 B.2.5 C.3 D.3.5
【解析】选C.∵D是△ABC的重心,
∴AE是BC边的中线,E是BC的中点,
又∵BC=6,
∴EC=×6=3.
二、填空题(每小题5分,共25分)
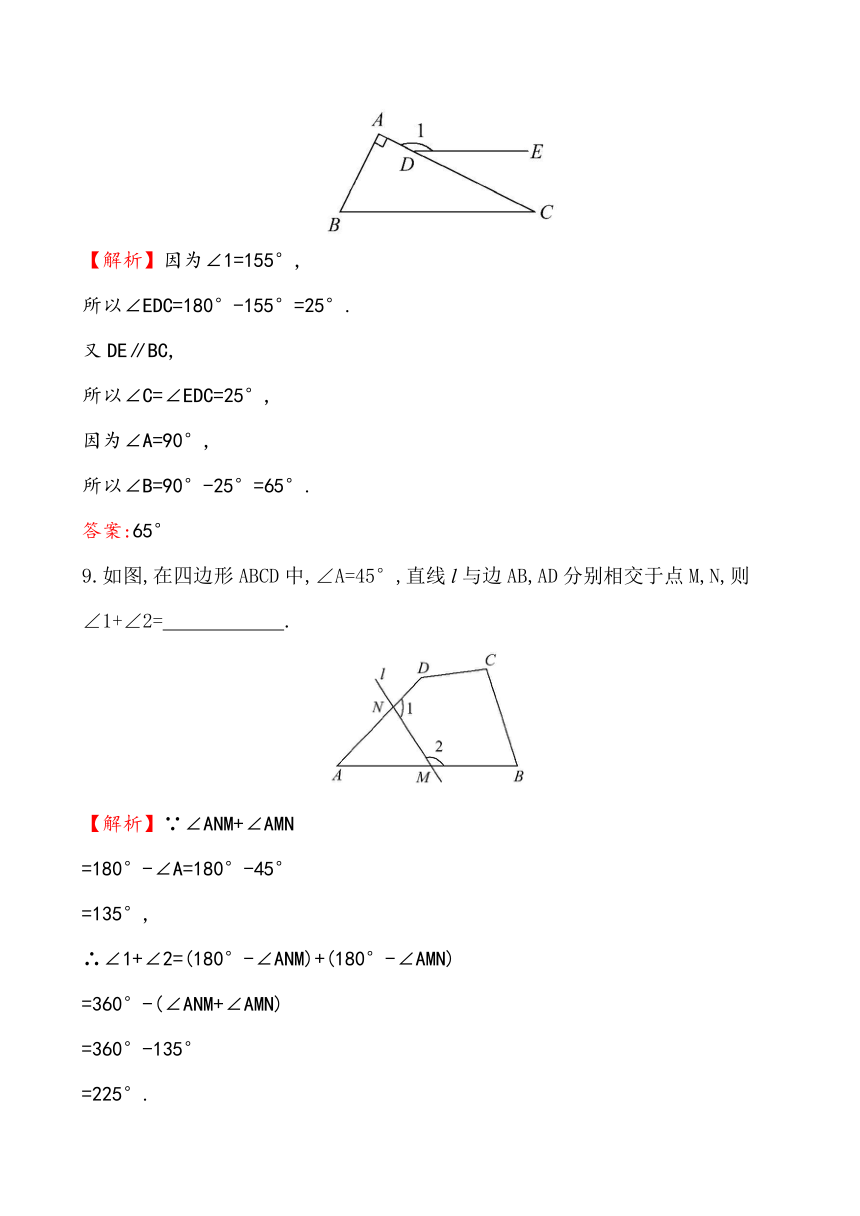
8.如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为 .
【解析】因为∠1=155°,
所以∠EDC=180°-155°=25°.
又DE∥BC,
所以∠C=∠EDC=25°,
因为∠A=90°,
所以∠B=90°-25°=65°.
答案:65°
9.如图,在四边形ABCD中,∠A=45°,直线l与边AB,AD分别相交于点M,N,则
∠1+∠2= .
【解析】∵∠ANM+∠AMN
=180°-∠A=180°-45°
=135°,
∴∠1+∠2=(180°-∠ANM)+(180°-∠AMN)
=360°-(∠ANM+∠AMN)
=360°-135°
=225°.
答案:225°
10.五边形的外角和等于 .
【解析】因为多边形的外角和为360°,所以五边形的外角和为360°.
答案:360°
11.如图,△ABC三边的中线AD,BE,CF的公共点为G,若S△ABC=12,则图中阴影部分面积是 .
【解析】由中线性质,可得AG=2GD,
则S△BGF=S△CGE=S△ABG
=×S△ABD
=××S△ABC
=×12=2,
∴阴影部分的面积为4.
答案:4
12.如图是用形状、大小完全相同的等腰梯形铺成的图案,则这个图案中的等腰梯形的底角(指钝角)是 度.
【解析】根据条件可知等腰梯形的三个钝角的和是360°,因而这个图案中等腰梯形的底角是360°÷3=120°.
答案:120
三、解答题(共47分)
13.(10分)在△ABC中,已知∠A=∠B=∠C,试判断三角形的形状.
【解析】由题意,设∠C=6x,
则∠B=4x,∠A=2x,
则6x+4x+2x=180°,∴x=15°,
∴最大角为∠C=6x=90°,
则三角形的形状是直角三角形.
14.(12分)在三角形ABC中,AE平分∠BAC,∠C>∠B,且FD⊥BC于D点.
(1)试推出∠EFD,∠B,∠C的关系.
(2)当点F在AE的延长线上时,其余条件不变,你在题(1)推导的结论还成立吗 说明理由.
【解析】(1)∠EFD=∠C-∠B,
理由如下:
由三角形的外角性质知:
∠FED=∠B+∠BAC,
故∠B+∠BAC+∠EFD=90°; ①
在△ABC中,由三角形的内角和定理得:
∠B+∠BAC+∠C=180°,
即:∠B+∠BAC+∠C=90°, ②
②-①,得:∠EFD=∠C-∠B.
(2)成立.理由:∵AE平分∠BAC,
∴∠FAC=∠BAC,
∵∠FED=∠B+∠FAB
=∠B+∠BAC,
且∠FED=90°-∠EFD,
∴90°-∠EFD
=∠B+∠BAC,
∴90°-∠EFD
=∠B+(180°-∠B-∠C),
∴∠EFD=∠C-∠B.
15.(12分)看图回答问题:
(1)内角和为2005°,小明为什么说不可能
(2)小华求的是几边形的内角和
(3)错把外角当内角的那个外角的度数你能求吗 是多少度呢
【解析】(1)∵2005°不是180°的整数倍,
∴小明说不可能.
(2)依题意有(x-2)·180°=2005°,
解得x≈13.1389.
因而多边形的边数是13,小华求的是十三边形的内角和.
(3)十三边形的内角和是(13-2)×180°=1980°,
则错把外角当内角的那个外角的度数是2005°-1980°=25°.
16.(13分)认真阅读下面关于三角形内外角平分线所夹角的大小的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线,
∴∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB),
又∵∠ABC+∠ACB=180°-∠A,
∴∠1+∠2=(180°-∠A)=90°-∠A,
∴∠BOC=180°-(∠1+∠2)=180°-=90°+∠A.
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系 请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系 (只写结论,不需证明)
结论: .
【解析】探究2结论:∠BOC=∠A.
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=∠ABC,∠2=∠ACD,
又∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠ABC,
∴∠2=(∠A+∠ABC)=∠A+∠1,
∵∠2是△BOC的一个外角,
∴∠BOC=∠2-∠1=∠A+∠1-∠1=∠A.
探究3:结论:∠BOC=90°-∠A.
理由如下:
∠OBC=(∠A+∠ACB),
∠OCB=(∠A+∠ABC),
∠BOC=180°-∠OBC-∠OCB
=180°-(∠A+∠ACB)-(∠A+∠ABC)
=180°-∠A-(∠A+∠ABC+∠ACB)
=90°-∠A.
(45分钟 100分)
一、选择题(每小题4分,共28分)
1.不一定在三角形内部的线段是 ( )
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.以上都不对
【解析】选C.锐角三角形的三条高在三角形内部,直角三角形的两条直角边也是三角形的高,钝角三角形有两条高在三角形外部.
2.已知△ABC的一个外角为50°,则△ABC一定是 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.锐角三角形或钝角三角形
【解析】选B.一个外角为50°,所以与它相邻的内角的度数为130°,所以三角形为钝角三角形.
【方法技巧】已知三角形的外角判断三角形的形状
1.三角形的外角有一个锐角,则此三角形一定是钝角三角形.
2.三角形的外角有一个直角,则此三角形一定是直角三角形.
3.三角形的外角都是钝角,则此三角形一定是锐角三角形.
3.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是 ( )
A.5 B.6 C.11 D.16
【解析】选C.因为已知三角形两边的长分别是4和10,所以第三边x的范围是6
【解析】因为已知三角形两边的长分别是2和6,
所以第三边x的范围是4
所以第三边的长为6.
答案:6
4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的
是 ( )
【解析】选A.根据三角形高的定义进行判断.
5.已知等腰三角形三边中有两边的长分别为4,9,则这个等腰三角形的周长
为 ( )
A.13 B.17
C.22 D.17或22
【解析】选C.当4为底时,其他两边都为9,
∵9,9,4可以构成三角形,
∴三角形的周长为22;
当4为腰时,其他两边为9和4,
∵4+4=8<9,∴不能构成三角形,故舍去.
6.如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数
是 ( )
A.75° B.55° C.40° D.35°
【解析】选C.两直线平行,同位角相等,三角形的一个外角等于与它不相邻的两个内角之和,所以75°=∠2+∠3,所以∠3=40°.
7.如图,△ABC中,D是△ABC的重心,连结AD并延长交BC于点E,若BC=6,则EC= ( )
A.2 B.2.5 C.3 D.3.5
【解析】选C.∵D是△ABC的重心,
∴AE是BC边的中线,E是BC的中点,
又∵BC=6,
∴EC=×6=3.
二、填空题(每小题5分,共25分)
8.如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为 .
【解析】因为∠1=155°,
所以∠EDC=180°-155°=25°.
又DE∥BC,
所以∠C=∠EDC=25°,
因为∠A=90°,
所以∠B=90°-25°=65°.
答案:65°
9.如图,在四边形ABCD中,∠A=45°,直线l与边AB,AD分别相交于点M,N,则
∠1+∠2= .
【解析】∵∠ANM+∠AMN
=180°-∠A=180°-45°
=135°,
∴∠1+∠2=(180°-∠ANM)+(180°-∠AMN)
=360°-(∠ANM+∠AMN)
=360°-135°
=225°.
答案:225°
10.五边形的外角和等于 .
【解析】因为多边形的外角和为360°,所以五边形的外角和为360°.
答案:360°
11.如图,△ABC三边的中线AD,BE,CF的公共点为G,若S△ABC=12,则图中阴影部分面积是 .
【解析】由中线性质,可得AG=2GD,
则S△BGF=S△CGE=S△ABG
=×S△ABD
=××S△ABC
=×12=2,
∴阴影部分的面积为4.
答案:4
12.如图是用形状、大小完全相同的等腰梯形铺成的图案,则这个图案中的等腰梯形的底角(指钝角)是 度.
【解析】根据条件可知等腰梯形的三个钝角的和是360°,因而这个图案中等腰梯形的底角是360°÷3=120°.
答案:120
三、解答题(共47分)
13.(10分)在△ABC中,已知∠A=∠B=∠C,试判断三角形的形状.
【解析】由题意,设∠C=6x,
则∠B=4x,∠A=2x,
则6x+4x+2x=180°,∴x=15°,
∴最大角为∠C=6x=90°,
则三角形的形状是直角三角形.
14.(12分)在三角形ABC中,AE平分∠BAC,∠C>∠B,且FD⊥BC于D点.
(1)试推出∠EFD,∠B,∠C的关系.
(2)当点F在AE的延长线上时,其余条件不变,你在题(1)推导的结论还成立吗 说明理由.
【解析】(1)∠EFD=∠C-∠B,
理由如下:
由三角形的外角性质知:
∠FED=∠B+∠BAC,
故∠B+∠BAC+∠EFD=90°; ①
在△ABC中,由三角形的内角和定理得:
∠B+∠BAC+∠C=180°,
即:∠B+∠BAC+∠C=90°, ②
②-①,得:∠EFD=∠C-∠B.
(2)成立.理由:∵AE平分∠BAC,
∴∠FAC=∠BAC,
∵∠FED=∠B+∠FAB
=∠B+∠BAC,
且∠FED=90°-∠EFD,
∴90°-∠EFD
=∠B+∠BAC,
∴90°-∠EFD
=∠B+(180°-∠B-∠C),
∴∠EFD=∠C-∠B.
15.(12分)看图回答问题:
(1)内角和为2005°,小明为什么说不可能
(2)小华求的是几边形的内角和
(3)错把外角当内角的那个外角的度数你能求吗 是多少度呢
【解析】(1)∵2005°不是180°的整数倍,
∴小明说不可能.
(2)依题意有(x-2)·180°=2005°,
解得x≈13.1389.
因而多边形的边数是13,小华求的是十三边形的内角和.
(3)十三边形的内角和是(13-2)×180°=1980°,
则错把外角当内角的那个外角的度数是2005°-1980°=25°.
16.(13分)认真阅读下面关于三角形内外角平分线所夹角的大小的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线,
∴∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB),
又∵∠ABC+∠ACB=180°-∠A,
∴∠1+∠2=(180°-∠A)=90°-∠A,
∴∠BOC=180°-(∠1+∠2)=180°-=90°+∠A.
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系 请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系 (只写结论,不需证明)
结论: .
【解析】探究2结论:∠BOC=∠A.
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=∠ABC,∠2=∠ACD,
又∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠ABC,
∴∠2=(∠A+∠ABC)=∠A+∠1,
∵∠2是△BOC的一个外角,
∴∠BOC=∠2-∠1=∠A+∠1-∠1=∠A.
探究3:结论:∠BOC=90°-∠A.
理由如下:
∠OBC=(∠A+∠ACB),
∠OCB=(∠A+∠ABC),
∠BOC=180°-∠OBC-∠OCB
=180°-(∠A+∠ACB)-(∠A+∠ABC)
=180°-∠A-(∠A+∠ABC+∠ACB)
=90°-∠A.
