第三章 交变电流 第一节 认识交变电流 课时训练(有解析)高中物理粤教版选择性必修第二册
文档属性
| 名称 | 第三章 交变电流 第一节 认识交变电流 课时训练(有解析)高中物理粤教版选择性必修第二册 |
|
|
| 格式 | docx | ||
| 文件大小 | 197.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-25 12:14:08 | ||
图片预览


文档简介
第三章 交变电流 第一节 认识交变电流
基础对点练
1.关于交变电流的理解,下列说法正确的是( )
A.如果电流大小随时间做周期性变化,则一定是交变电流
B.交变电流一定是按正弦规律变化的
C.交变电流电压的大小和方向随时间做周期性变化
D.化学电池提供的电流也可能是交变电流
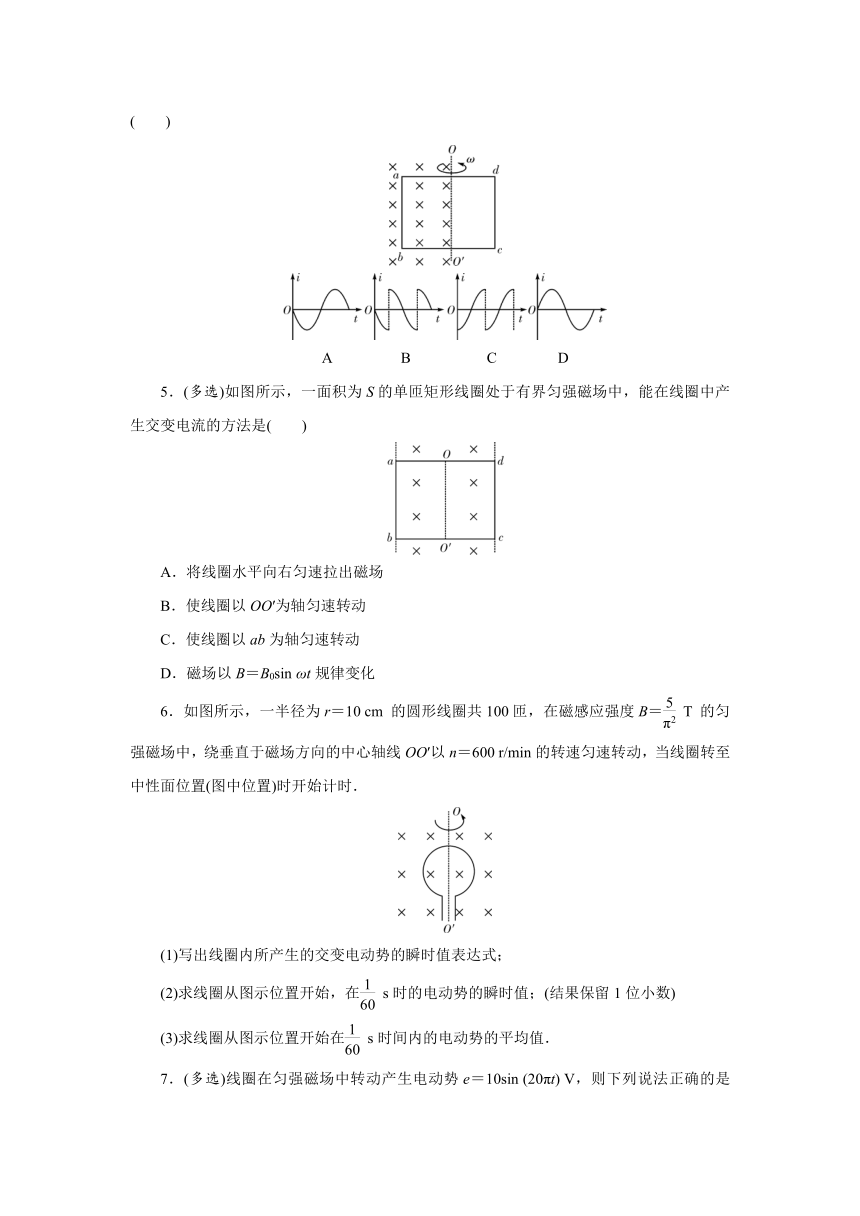
2.下列关于电流i随时间t变化的图像中,不表示交变电流的是( )
A B
C D
3.交流发电机的示意图如图所示,线圈ABCD绕垂直于磁场方向的转轴OO′匀速转动.在图示位置,下列说法正确的是( )
A.穿过线圈的磁通量变化率最小
B.线圈中电流方向将发生改变
C.线圈中电流最大,方向为B→A
D.穿过线圈的磁通量最大
4.如图所示,单匝矩形线圈的一半放在具有理想边界的匀强磁场中,线圈轴线OO′与磁场边界重合,线圈按图示方向匀速转动(ab边向纸外,cd边向纸内).若从图示位置开始计时,并规定电流方向沿a→b→c→d→a为正方向,则线圈内感应电流随时间变化的图像是图中的( )
A B C D
5.(多选)如图所示,一面积为S的单匝矩形线圈处于有界匀强磁场中,能在线圈中产生交变电流的方法是( )
A.将线圈水平向右匀速拉出磁场
B.使线圈以OO′为轴匀速转动
C.使线圈以ab为轴匀速转动
D.磁场以B=B0sin ωt规律变化
6.如图所示,一半径为r=10 cm 的圆形线圈共100匝,在磁感应强度B= T 的匀强磁场中,绕垂直于磁场方向的中心轴线OO′以n=600 r/min的转速匀速转动,当线圈转至中性面位置(图中位置)时开始计时.
(1)写出线圈内所产生的交变电动势的瞬时值表达式;
(2)求线圈从图示位置开始,在 s时的电动势的瞬时值;(结果保留1位小数)
(3)求线圈从图示位置开始在 s时间内的电动势的平均值.
7.(多选)线圈在匀强磁场中转动产生电动势e=10sin (20πt) V,则下列说法正确的是( )
A.t=0时,线圈平面位于中性面
B.t=0时,穿过线圈的磁通量最大
C.t=0时,导线切割磁感线的有效速率最大
D.t=0.4 s时,e有最大值10 V
8.矩形线圈的匝数为50匝,在匀强磁场中绕垂直于磁场的轴匀速转动,穿过线圈的磁通量Φ随时间t的变化规律如图所示,则( )
A.在t=0.1 s和t=0.3 s时,电动势最大
B.在t=0.1 s和t=0.3 s时,线圈与中性面垂直
C.在t=0.2 s和t=0.4 s时,磁通量变化率最大
D.在t=0.2 s和t=0.4 s时,电动势改变方向
综合提升练
9.如图甲所示,矩形线圈在匀强磁场中绕垂直于磁感线的中心轴OO′匀速转动,从某时刻开始计时,产生的感应电动势e随时间t的变化曲线如图乙所示,若线圈匝数N=100匝,外接电阻R=70 Ω,线圈电阻r=10 Ω,则下列说法正确的是( )
A.通过线圈的最大电流为1.25 A
B.线圈的角速度为50 rad/s
C.电压表的示数为50 V
D.穿过线圈的最大磁通量为 Wb
10.如图所示,线圈abcd的面积是0.05 m2,共100匝,线圈的总电阻r=1 Ω,外接电阻R=9 Ω,匀强磁场的磁感应强度B= T,线圈以角速度ω=100π rad/s匀速转动.
(1)若从线圈经过图示位置(线圈平面与磁感线垂直)时开始计时,写出线圈中感应电动势瞬时值的表达式.
(2)写出交变电流的瞬时值表达式.
(3)求线圈由图示位置转过的过程中,交变电动势的平均值.
答案解析
1、【答案】C 【解析】交变电流电压和电流的大小和方向随时间做周期性变化,A错误,C正确;交变电流不一定是按正弦规律变化,B错误;化学电池提供的电流是直流电,D错误.
2、【答案】A 【解析】A图中电流大小发生周期性变化,但方向保持不变,所以不是交变电流,A正确;B、C、D图中电流大小、方向均发生周期性变化,均是交变电流,B、C、D错误.
3、【答案】C 【解析】在图示位置,线圈平面与磁场平行,穿过线圈的磁通量为零,穿过线圈的磁通量变化率最大,A、D错误;当线圈在中性面时,线圈平面与磁场垂直,线圈中电流方向将发生改变,B错误;由右手定则可知线圈中电流最大,方向为B→A,C正确.
4、【答案】A 【解析】由题意知线圈总有一半在磁场中做切割磁感线运动,所以产生的仍然是正弦式交变电流,只是感应电动势最大值为全部线圈在磁场中匀速转动时产生的感应电动势最大值的一半,故B、C错误.再由楞次定律及安培定则可以判断出A正确,D错误.
5、【答案】BCD 【解析】将线圈向右匀速拉出磁场的过程中磁通量均匀减小,因此产生的感应电流大小不变,A错误;线圈绕垂直于磁感线方向的轴转动时磁通量发生周期性变化,因此产生交变电流,B、C正确;如果磁感应强度发生周期性变化,而线圈面积不变,则磁通量也发生周期性变化,产生交变电流,D正确.
6、解:线圈在匀强磁场中绕垂直于磁场方向的轴线匀速转动时,线圈内产生正弦式交变电动势,当线圈平面在中性面时开始计时,其表达式为e=Emsin ωt,而在某段时间内的平均电动势可根据=N求得.
(1)e=Emsin ωt,Em=NBSω(与线圈形状无关),
又ω=2πn= rad/s=20π rad/s,
故e=100sin (20πt) V.
(2)当t= s时,
e=100sin V=50 V≈86.6 V.
(3)在 s内线圈转过的角度θ=ωt=20π× rad= rad,
由Φ=BS cos ωt知ΔΦ=BS,
所以=N= V.
7、【答案】AB 【解析】由电动势的瞬时值表达式可知,计时从线圈位于中性面时开始,所以t=0时,线圈平面位于中性面,磁通量最大,但此时导线切割磁感线的有效速率为零,A、B正确,C错误.当t=0.4 s时,e=10sin 8π=0,D错误.
8、【答案】C 【解析】在t=0.1 s和t=0.3 s时,线圈中磁通量最大,线圈处于中性面位置,磁通量的变化率为零,感应电动势为零,A、B错误;t=0.2 s和t=0.4 s时,线圈中磁通量为零,此时刻磁通量的变化率最大,感应电动势最大,Φ-t图像斜率不变,电动势方向不变,C正确,D错误.故选C.
9、【答案】A 【解析】根据闭合电路的欧姆定律可知Im== A=1.25 A,即通过线圈的最大电流为1.25 A,电压表测量的是有效值,故有电压表的示数为U=R≈61.9 V,故A正确,C错误;由乙图可知周期T=0.04 s,转动的角速度为ω==50π rad/s,故B错误;根据Em=NBSω,可得穿过线圈的最大磁通量为Φ=BS== Wb,故D错误.
10、解:(1)线圈中感应电动势的最大值为
Em=NBSω=100××0.05×100π V=500 V,
线圈中感应电动势瞬时值e=Emsin ωt.
所以e=500sin (100πt) V.
(2)交变电流的最大值Im== A=50 A,
所以交变电流的瞬时值表达式为i=50sin (100πt) A.
(3)=N== V.
基础对点练
1.关于交变电流的理解,下列说法正确的是( )
A.如果电流大小随时间做周期性变化,则一定是交变电流
B.交变电流一定是按正弦规律变化的
C.交变电流电压的大小和方向随时间做周期性变化
D.化学电池提供的电流也可能是交变电流
2.下列关于电流i随时间t变化的图像中,不表示交变电流的是( )
A B
C D
3.交流发电机的示意图如图所示,线圈ABCD绕垂直于磁场方向的转轴OO′匀速转动.在图示位置,下列说法正确的是( )
A.穿过线圈的磁通量变化率最小
B.线圈中电流方向将发生改变
C.线圈中电流最大,方向为B→A
D.穿过线圈的磁通量最大
4.如图所示,单匝矩形线圈的一半放在具有理想边界的匀强磁场中,线圈轴线OO′与磁场边界重合,线圈按图示方向匀速转动(ab边向纸外,cd边向纸内).若从图示位置开始计时,并规定电流方向沿a→b→c→d→a为正方向,则线圈内感应电流随时间变化的图像是图中的( )
A B C D
5.(多选)如图所示,一面积为S的单匝矩形线圈处于有界匀强磁场中,能在线圈中产生交变电流的方法是( )
A.将线圈水平向右匀速拉出磁场
B.使线圈以OO′为轴匀速转动
C.使线圈以ab为轴匀速转动
D.磁场以B=B0sin ωt规律变化
6.如图所示,一半径为r=10 cm 的圆形线圈共100匝,在磁感应强度B= T 的匀强磁场中,绕垂直于磁场方向的中心轴线OO′以n=600 r/min的转速匀速转动,当线圈转至中性面位置(图中位置)时开始计时.
(1)写出线圈内所产生的交变电动势的瞬时值表达式;
(2)求线圈从图示位置开始,在 s时的电动势的瞬时值;(结果保留1位小数)
(3)求线圈从图示位置开始在 s时间内的电动势的平均值.
7.(多选)线圈在匀强磁场中转动产生电动势e=10sin (20πt) V,则下列说法正确的是( )
A.t=0时,线圈平面位于中性面
B.t=0时,穿过线圈的磁通量最大
C.t=0时,导线切割磁感线的有效速率最大
D.t=0.4 s时,e有最大值10 V
8.矩形线圈的匝数为50匝,在匀强磁场中绕垂直于磁场的轴匀速转动,穿过线圈的磁通量Φ随时间t的变化规律如图所示,则( )
A.在t=0.1 s和t=0.3 s时,电动势最大
B.在t=0.1 s和t=0.3 s时,线圈与中性面垂直
C.在t=0.2 s和t=0.4 s时,磁通量变化率最大
D.在t=0.2 s和t=0.4 s时,电动势改变方向
综合提升练
9.如图甲所示,矩形线圈在匀强磁场中绕垂直于磁感线的中心轴OO′匀速转动,从某时刻开始计时,产生的感应电动势e随时间t的变化曲线如图乙所示,若线圈匝数N=100匝,外接电阻R=70 Ω,线圈电阻r=10 Ω,则下列说法正确的是( )
A.通过线圈的最大电流为1.25 A
B.线圈的角速度为50 rad/s
C.电压表的示数为50 V
D.穿过线圈的最大磁通量为 Wb
10.如图所示,线圈abcd的面积是0.05 m2,共100匝,线圈的总电阻r=1 Ω,外接电阻R=9 Ω,匀强磁场的磁感应强度B= T,线圈以角速度ω=100π rad/s匀速转动.
(1)若从线圈经过图示位置(线圈平面与磁感线垂直)时开始计时,写出线圈中感应电动势瞬时值的表达式.
(2)写出交变电流的瞬时值表达式.
(3)求线圈由图示位置转过的过程中,交变电动势的平均值.
答案解析
1、【答案】C 【解析】交变电流电压和电流的大小和方向随时间做周期性变化,A错误,C正确;交变电流不一定是按正弦规律变化,B错误;化学电池提供的电流是直流电,D错误.
2、【答案】A 【解析】A图中电流大小发生周期性变化,但方向保持不变,所以不是交变电流,A正确;B、C、D图中电流大小、方向均发生周期性变化,均是交变电流,B、C、D错误.
3、【答案】C 【解析】在图示位置,线圈平面与磁场平行,穿过线圈的磁通量为零,穿过线圈的磁通量变化率最大,A、D错误;当线圈在中性面时,线圈平面与磁场垂直,线圈中电流方向将发生改变,B错误;由右手定则可知线圈中电流最大,方向为B→A,C正确.
4、【答案】A 【解析】由题意知线圈总有一半在磁场中做切割磁感线运动,所以产生的仍然是正弦式交变电流,只是感应电动势最大值为全部线圈在磁场中匀速转动时产生的感应电动势最大值的一半,故B、C错误.再由楞次定律及安培定则可以判断出A正确,D错误.
5、【答案】BCD 【解析】将线圈向右匀速拉出磁场的过程中磁通量均匀减小,因此产生的感应电流大小不变,A错误;线圈绕垂直于磁感线方向的轴转动时磁通量发生周期性变化,因此产生交变电流,B、C正确;如果磁感应强度发生周期性变化,而线圈面积不变,则磁通量也发生周期性变化,产生交变电流,D正确.
6、解:线圈在匀强磁场中绕垂直于磁场方向的轴线匀速转动时,线圈内产生正弦式交变电动势,当线圈平面在中性面时开始计时,其表达式为e=Emsin ωt,而在某段时间内的平均电动势可根据=N求得.
(1)e=Emsin ωt,Em=NBSω(与线圈形状无关),
又ω=2πn= rad/s=20π rad/s,
故e=100sin (20πt) V.
(2)当t= s时,
e=100sin V=50 V≈86.6 V.
(3)在 s内线圈转过的角度θ=ωt=20π× rad= rad,
由Φ=BS cos ωt知ΔΦ=BS,
所以=N= V.
7、【答案】AB 【解析】由电动势的瞬时值表达式可知,计时从线圈位于中性面时开始,所以t=0时,线圈平面位于中性面,磁通量最大,但此时导线切割磁感线的有效速率为零,A、B正确,C错误.当t=0.4 s时,e=10sin 8π=0,D错误.
8、【答案】C 【解析】在t=0.1 s和t=0.3 s时,线圈中磁通量最大,线圈处于中性面位置,磁通量的变化率为零,感应电动势为零,A、B错误;t=0.2 s和t=0.4 s时,线圈中磁通量为零,此时刻磁通量的变化率最大,感应电动势最大,Φ-t图像斜率不变,电动势方向不变,C正确,D错误.故选C.
9、【答案】A 【解析】根据闭合电路的欧姆定律可知Im== A=1.25 A,即通过线圈的最大电流为1.25 A,电压表测量的是有效值,故有电压表的示数为U=R≈61.9 V,故A正确,C错误;由乙图可知周期T=0.04 s,转动的角速度为ω==50π rad/s,故B错误;根据Em=NBSω,可得穿过线圈的最大磁通量为Φ=BS== Wb,故D错误.
10、解:(1)线圈中感应电动势的最大值为
Em=NBSω=100××0.05×100π V=500 V,
线圈中感应电动势瞬时值e=Emsin ωt.
所以e=500sin (100πt) V.
(2)交变电流的最大值Im== A=50 A,
所以交变电流的瞬时值表达式为i=50sin (100πt) A.
(3)=N== V.
同课章节目录
- 第一章 磁场
- 第一节 安培力
- 第二节 安培力的应用
- 第三节 洛伦兹力
- 第四节 洛伦兹力与现代技术
- 第二章 电磁感应
- 第一节 感应电流的方向
- 第二节 法拉第电磁感应定律
- 第三节 电磁感应定律的应用
- 第四节 互感和自感
- 第五节 涡流现象及其应用
- 第三章 交变电流
- 第一节 认识交变电流
- 第二节 描述交变电流的物理量
- 第三节 变压器
- 第四节 远距离输电
- 第四章 电磁震荡与电磁波
- 第一节 电磁振动
- 第二节 麦克斯韦电磁电磁场理论
- 第三节 电磁波的发射、传播和接收
- 第四节 电磁波谱
- 第五章 传感器
- 第一节 传感器及其工作原理
- 第二节 传感器的应用
- 第三节 用传感器制作自动控制装置
- 第四节 利用智能手机中的磁传感器研究磁现象
