导数的概念
图片预览

文档简介
导数的概念及运算
一、复习目标:1.了解导数概念的实际背景;2.理解导数的几何意义;
3.能根据导数定义,求函数的导数;
4.能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,能求简单的复合函数(仅限于形如f(ax+b))的导数。
二、主要知识及主要方法:
函数在处导数的定义:
导数的几何意义:
导数是函数在点的处瞬时变化率,它反映的函数在点处变化的快慢程度.
它的几何意义是曲线上点()处的切线的斜率.因此,如果在点可导,则曲线在点()处的切线方程为
导函数(导数):如果函数在开区间内的每点处都有导数,此时对于每一个,都对应着一个确定的导数,从而构成了一个新的函数, 称这个函数为函数在开区间内的导函数,简称导数,也可记作,即==
函数在处的导数就是函数在开区间上导数在处的函数值,即=.所以函数在处的导数也记作
4,几种常见函数的导数: (为常数);();
; ;; , ;
5,求导法则:法则
法则 ,
法则:
6,复合函数的导数:设函数在点处有导数,函数在点的对应点处有导数,则复合函数在点x处也有导数,且 或
三、典例分析:
例1.已知,求
(2)设,求;
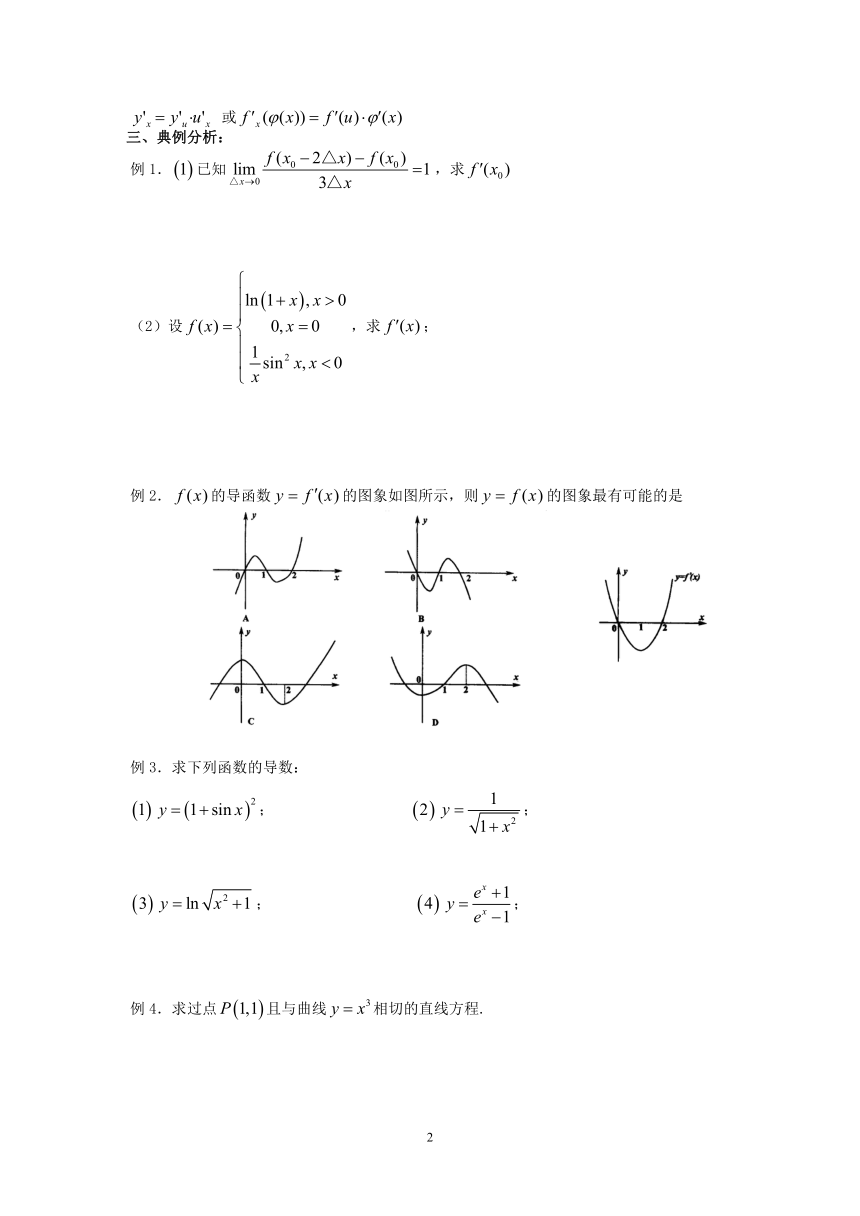
例2.的导函数的图象如图所示,则的图象最有可能的是
例3.求下列函数的导数:
; ;
; ;
例4.求过点且与曲线相切的直线方程.
例5.(1)已知函数在R上满足,则曲线在点处的切线方程是 ( )(B) (C) (D)
(2)设函数,曲线在点处的切线方程为,则曲线在点处切线的斜率为( )A. B. C. D.
(3)已知二次函数的导函数的图像与直线平行,且在=-1处取得最小值m-1(m).设函数
(1)若曲线上的点P到点Q(0,2)的距离的最小值为,求m的值
(2) 如何取值时,函数存在零点,并求出零点.
四、针对练习:
1(安徽)若曲线的一条切线与直线垂直,则的方程为( )
;;;
2(全国Ⅱ文)过点作抛物线的切线,则其中一条切线为( )
3.(08全国)设曲线在点处的切线与直线垂直,则( )
A.2 B. C. D.
4(湖南)设,,,…,,,则 ( )
5(江西)对于上可导的任意函数,若满足≥,则必有( )
≤
≥
5若,则=
6(届高三皖南八校联考)已知,则
7已知函数,则
8求下列函数的导数:
; (3); (4)
五、走向高考:
1(安徽)若曲线的一条切线与直线垂直,则的方程为( )
;;;
2(海南)曲线在点处的切线与坐标轴所围三角形的面积为( )
3(09江西)若存在过点的直线与曲线和都相切,则等于
A.或 B.或 C.或 D.或
4(全国)设函数(),若是奇函数,
则
5(湖北文)已知函数的图象在点处的切线方程是,则
6(安徽)对正整数,设曲线在处的切线与轴交点的纵坐标为,则数列的前项和的公式是
PAGE
1
一、复习目标:1.了解导数概念的实际背景;2.理解导数的几何意义;
3.能根据导数定义,求函数的导数;
4.能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,能求简单的复合函数(仅限于形如f(ax+b))的导数。
二、主要知识及主要方法:
函数在处导数的定义:
导数的几何意义:
导数是函数在点的处瞬时变化率,它反映的函数在点处变化的快慢程度.
它的几何意义是曲线上点()处的切线的斜率.因此,如果在点可导,则曲线在点()处的切线方程为
导函数(导数):如果函数在开区间内的每点处都有导数,此时对于每一个,都对应着一个确定的导数,从而构成了一个新的函数, 称这个函数为函数在开区间内的导函数,简称导数,也可记作,即==
函数在处的导数就是函数在开区间上导数在处的函数值,即=.所以函数在处的导数也记作
4,几种常见函数的导数: (为常数);();
; ;; , ;
5,求导法则:法则
法则 ,
法则:
6,复合函数的导数:设函数在点处有导数,函数在点的对应点处有导数,则复合函数在点x处也有导数,且 或
三、典例分析:
例1.已知,求
(2)设,求;
例2.的导函数的图象如图所示,则的图象最有可能的是
例3.求下列函数的导数:
; ;
; ;
例4.求过点且与曲线相切的直线方程.
例5.(1)已知函数在R上满足,则曲线在点处的切线方程是 ( )(B) (C) (D)
(2)设函数,曲线在点处的切线方程为,则曲线在点处切线的斜率为( )A. B. C. D.
(3)已知二次函数的导函数的图像与直线平行,且在=-1处取得最小值m-1(m).设函数
(1)若曲线上的点P到点Q(0,2)的距离的最小值为,求m的值
(2) 如何取值时,函数存在零点,并求出零点.
四、针对练习:
1(安徽)若曲线的一条切线与直线垂直,则的方程为( )
;;;
2(全国Ⅱ文)过点作抛物线的切线,则其中一条切线为( )
3.(08全国)设曲线在点处的切线与直线垂直,则( )
A.2 B. C. D.
4(湖南)设,,,…,,,则 ( )
5(江西)对于上可导的任意函数,若满足≥,则必有( )
≤
≥
5若,则=
6(届高三皖南八校联考)已知,则
7已知函数,则
8求下列函数的导数:
; (3); (4)
五、走向高考:
1(安徽)若曲线的一条切线与直线垂直,则的方程为( )
;;;
2(海南)曲线在点处的切线与坐标轴所围三角形的面积为( )
3(09江西)若存在过点的直线与曲线和都相切,则等于
A.或 B.或 C.或 D.或
4(全国)设函数(),若是奇函数,
则
5(湖北文)已知函数的图象在点处的切线方程是,则
6(安徽)对正整数,设曲线在处的切线与轴交点的纵坐标为,则数列的前项和的公式是
PAGE
1
