《2.2.3 一元二次不等式的解法》教学设计(表格式)
文档属性
| 名称 | 《2.2.3 一元二次不等式的解法》教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 173.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 22:47:53 | ||
图片预览


文档简介
《一元二次不等式的解法》教学设计
学情分析 在初中的学习中,我们的学生对一元二次方程和函数已经有所了解,在老师的引导下,能够解决一般的问题。但是,对于一元二次方程的灵活求解,选择合理的方法对我们学生来说是一个难点,我们的学生因为使用计算器,对解一元二次方程的其他方法的应用不熟悉,只懂得简单的公式计算,尤其是十字相乘法,是学生解题时的短板。而本节解方程是必要步骤之一,所以解决好科学的解一元二次方程,是取得良好教学效果的关键。
学习目标 知识与技能 复习与巩固一元二次方程的解法;更进一步的了解与巩固一元二次函数及其图像;一元二次不等式的解法;
过程与方法 结合一元二次函数图像,探索一元二次不等式与一元二次函数的关系,然后归纳总结一元二次不等式的解法。
情感态度与价值观 认知函数与不等关系的联系,培养学生数形结合的思想。提升识图能力。
学习重点难点 重点:一元二次不等式的求解。难点:一元二次不等式的求解。
学习方法 结合函数图像,分析与探索,归纳总结得出解法,然后练习提高。
教学资源 教材,名师伴你行
教学过程(第 1 课时)
教学环节 教师活动 学生活动 教学预设
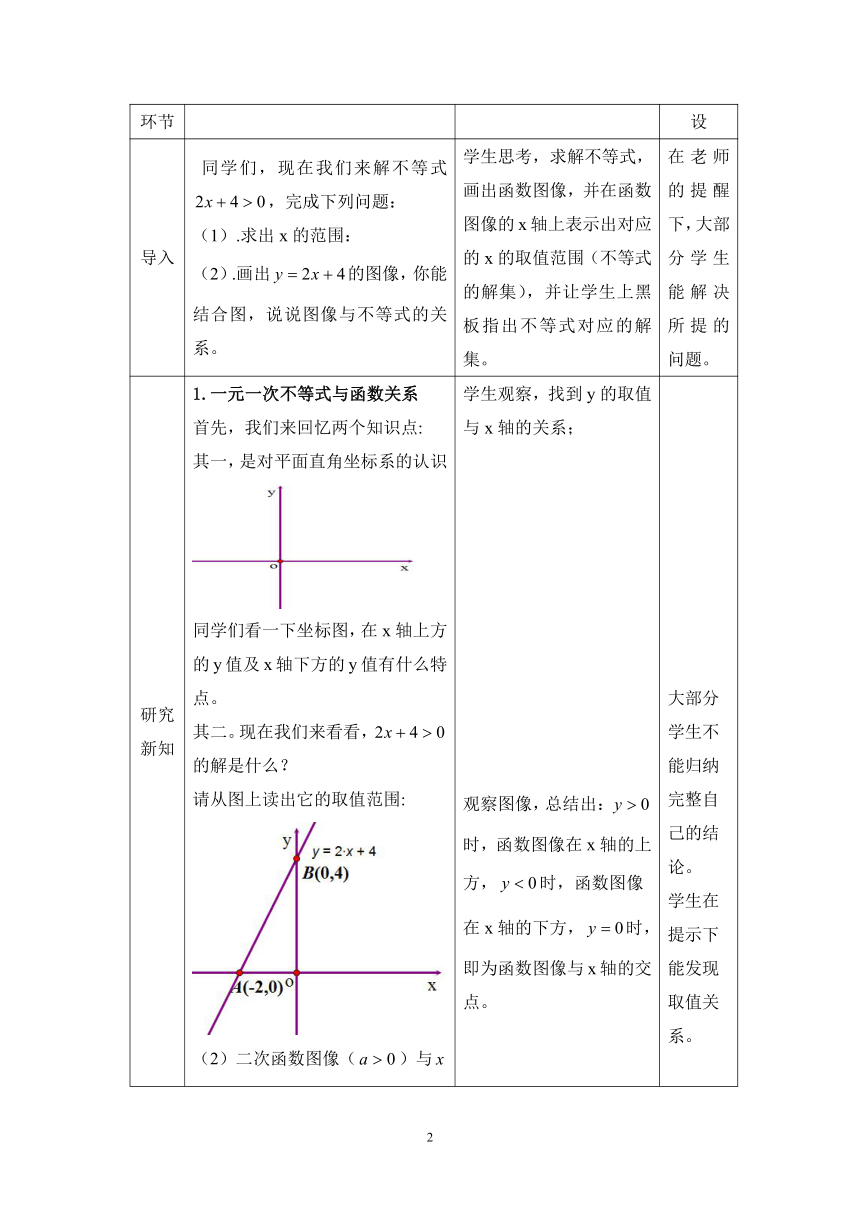
导入 同学们,现在我们来解不等式,完成下列问题:(1).求出x的范围:(2).画出的图像,你能结合图,说说图像与不等式的关系。 学生思考,求解不等式,画出函数图像,并在函数图像的x轴上表示出对应的x的取值范围(不等式的解集),并让学生上黑板指出不等式对应的解集。 在老师的提醒下,大部分学生能解决所提的问题。
研究新知 1.一元一次不等式与函数关系首先,我们来回忆两个知识点:其一,是对平面直角坐标系的认识同学们看一下坐标图,在x轴上方的y值及x轴下方的y值有什么特点。其二。现在我们来看看,的解是什么?请从图上读出它的取值范围:(2)二次函数图像()与轴的关系及函数值的正负性。当时,图像如下:设x1,x2为函数对应方程的两根,即两根,现在我们来看看,当时,对应的的取值和当时,对应的的取值。 你们能用一句话来总结一下:“大于零,两根之外,小于零,两根之间”。现在()时的一元二次不等式你能求解吗?例:练习:下面我们来看一下和的情形,其图像如下,你们能说出这时候不等式的解吗?时,函数图像于x轴只有一个交点,这时,除外,其余的都在x轴的上方,所以“大于零,解集为,小于零无解。” 时,函数图像于x轴没有交点,图像都在x轴的上方,所以“大于或等于零,解集为,小于零无解。”到这里为止,我们已经解决时的一元二次不等式的求解方法,那么当时,我们怎么求解呢? 例如:.这个问题,留给大家在课下去讨论。下节课请同学们讲解讨论现在,我们来总结一下时解一元二次不等式的一般方法:第一步:,解对应的一元二次方程;第三步,当时,根据“大于零,两根之外,小于零,在两根之间”,写出不等式的解集;,则大于零的解集,小于零则无解;时,大于零的解集为,小于零则无解。3.练习巩固与学习提高: 学生观察,找到y的取值与x轴的关系;观察图像,总结出:时,函数图像在x轴的上方,时,函数图像在x轴的下方,时,即为函数图像与x轴的交点。观察图像,发现时对应的图像在抽上方。对应的取值范围为:;时对应的图像在抽上方。对应的取值范围为:。学生在引导下能基本总结出,“,大于零,两根之外,小于零两根之间”解:两根为的解集为:时,大于零,只要求,小于零无解。时,大于零解集为,小于零无解。学生在老师的提示下尝试归纳总结,口述出自己归纳的结论,可以在同学间讨论,彼此补充不足。学生自主练习,部分学生板书自己的做题步骤,然后一起找出解题的问题所在。或写出自己不同的解法。未完全理解的提问 大部分学生不能归纳完整自己的结论。学生在提示下能发现取值关系。提示:大于零时,取值在两根的两边,而小于零是,取值夹在两根之间。学生不能求解方程或是不能见解集写成集合提示:请同学们看看图像的特征。 对于时关注对称轴部分学生不能解出对应的方程或是很快地写出解集不能准确的归纳,需要给予提示。学生可能对大于零在两根之外,小于零在两根之间理解不够透彻,甚至会误解为其他意思,需要不断给予提示。
总结 解一元二次不等式时,在保证的情况下解对应的一元二次方程。在解方程中,若则大于零解集为,小于零无解;若,则大于零的解集为,小于零的无解;时根据“大于零,两根之外,小于零,在两根之间”,写出解集。 学生思考一段时间,之间进行总结。 学生能说出大概的内容,但是可能不完善。
作业布置 一、本堂课知识巩固 P53练习1
二、新知识预习 教材例3、例4,P80,习题A组5,6.求解:
反思 不 足 1.教学中应该注意板书,注重板书的设计,突出重难点;2.注重课堂礼仪,注意维护课堂纪律;3.讲课中没有注重从特殊到一般,尽量将例子从简单和易懂,有能体现学科知识为主;4.对重点知识应该,应该着重强调,讲解清晰,并且注重学生从感性的认识;进一步放开思想,让学生多参与课堂,多思考,增强课堂活力,注重数形结合。
再教设计 1.引入要从简单易懂的,让学生能从简单的知识中理解新知识点;2.要从特殊到一般,以一个简单的例子引入新知识点;3.要放开课堂,让学生多自学、思考,参与课堂;4.要丰富课堂,做到教学连贯,学生参与;5.要及时总结,突出重点。
PAGE
9
学情分析 在初中的学习中,我们的学生对一元二次方程和函数已经有所了解,在老师的引导下,能够解决一般的问题。但是,对于一元二次方程的灵活求解,选择合理的方法对我们学生来说是一个难点,我们的学生因为使用计算器,对解一元二次方程的其他方法的应用不熟悉,只懂得简单的公式计算,尤其是十字相乘法,是学生解题时的短板。而本节解方程是必要步骤之一,所以解决好科学的解一元二次方程,是取得良好教学效果的关键。
学习目标 知识与技能 复习与巩固一元二次方程的解法;更进一步的了解与巩固一元二次函数及其图像;一元二次不等式的解法;
过程与方法 结合一元二次函数图像,探索一元二次不等式与一元二次函数的关系,然后归纳总结一元二次不等式的解法。
情感态度与价值观 认知函数与不等关系的联系,培养学生数形结合的思想。提升识图能力。
学习重点难点 重点:一元二次不等式的求解。难点:一元二次不等式的求解。
学习方法 结合函数图像,分析与探索,归纳总结得出解法,然后练习提高。
教学资源 教材,名师伴你行
教学过程(第 1 课时)
教学环节 教师活动 学生活动 教学预设
导入 同学们,现在我们来解不等式,完成下列问题:(1).求出x的范围:(2).画出的图像,你能结合图,说说图像与不等式的关系。 学生思考,求解不等式,画出函数图像,并在函数图像的x轴上表示出对应的x的取值范围(不等式的解集),并让学生上黑板指出不等式对应的解集。 在老师的提醒下,大部分学生能解决所提的问题。
研究新知 1.一元一次不等式与函数关系首先,我们来回忆两个知识点:其一,是对平面直角坐标系的认识同学们看一下坐标图,在x轴上方的y值及x轴下方的y值有什么特点。其二。现在我们来看看,的解是什么?请从图上读出它的取值范围:(2)二次函数图像()与轴的关系及函数值的正负性。当时,图像如下:设x1,x2为函数对应方程的两根,即两根,现在我们来看看,当时,对应的的取值和当时,对应的的取值。 你们能用一句话来总结一下:“大于零,两根之外,小于零,两根之间”。现在()时的一元二次不等式你能求解吗?例:练习:下面我们来看一下和的情形,其图像如下,你们能说出这时候不等式的解吗?时,函数图像于x轴只有一个交点,这时,除外,其余的都在x轴的上方,所以“大于零,解集为,小于零无解。” 时,函数图像于x轴没有交点,图像都在x轴的上方,所以“大于或等于零,解集为,小于零无解。”到这里为止,我们已经解决时的一元二次不等式的求解方法,那么当时,我们怎么求解呢? 例如:.这个问题,留给大家在课下去讨论。下节课请同学们讲解讨论现在,我们来总结一下时解一元二次不等式的一般方法:第一步:,解对应的一元二次方程;第三步,当时,根据“大于零,两根之外,小于零,在两根之间”,写出不等式的解集;,则大于零的解集,小于零则无解;时,大于零的解集为,小于零则无解。3.练习巩固与学习提高: 学生观察,找到y的取值与x轴的关系;观察图像,总结出:时,函数图像在x轴的上方,时,函数图像在x轴的下方,时,即为函数图像与x轴的交点。观察图像,发现时对应的图像在抽上方。对应的取值范围为:;时对应的图像在抽上方。对应的取值范围为:。学生在引导下能基本总结出,“,大于零,两根之外,小于零两根之间”解:两根为的解集为:时,大于零,只要求,小于零无解。时,大于零解集为,小于零无解。学生在老师的提示下尝试归纳总结,口述出自己归纳的结论,可以在同学间讨论,彼此补充不足。学生自主练习,部分学生板书自己的做题步骤,然后一起找出解题的问题所在。或写出自己不同的解法。未完全理解的提问 大部分学生不能归纳完整自己的结论。学生在提示下能发现取值关系。提示:大于零时,取值在两根的两边,而小于零是,取值夹在两根之间。学生不能求解方程或是不能见解集写成集合提示:请同学们看看图像的特征。 对于时关注对称轴部分学生不能解出对应的方程或是很快地写出解集不能准确的归纳,需要给予提示。学生可能对大于零在两根之外,小于零在两根之间理解不够透彻,甚至会误解为其他意思,需要不断给予提示。
总结 解一元二次不等式时,在保证的情况下解对应的一元二次方程。在解方程中,若则大于零解集为,小于零无解;若,则大于零的解集为,小于零的无解;时根据“大于零,两根之外,小于零,在两根之间”,写出解集。 学生思考一段时间,之间进行总结。 学生能说出大概的内容,但是可能不完善。
作业布置 一、本堂课知识巩固 P53练习1
二、新知识预习 教材例3、例4,P80,习题A组5,6.求解:
反思 不 足 1.教学中应该注意板书,注重板书的设计,突出重难点;2.注重课堂礼仪,注意维护课堂纪律;3.讲课中没有注重从特殊到一般,尽量将例子从简单和易懂,有能体现学科知识为主;4.对重点知识应该,应该着重强调,讲解清晰,并且注重学生从感性的认识;进一步放开思想,让学生多参与课堂,多思考,增强课堂活力,注重数形结合。
再教设计 1.引入要从简单易懂的,让学生能从简单的知识中理解新知识点;2.要从特殊到一般,以一个简单的例子引入新知识点;3.要放开课堂,让学生多自学、思考,参与课堂;4.要丰富课堂,做到教学连贯,学生参与;5.要及时总结,突出重点。
PAGE
9
