几何概型复习

课件16张PPT。几何概型引入2.如图在线段 上任取一点 ，则 的概率为 .
0.70.7几何概型如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例,则称这样的概率模型为几何概型.几何概型的特点:(1)试验中所有可能出现的结果(基本事件)有
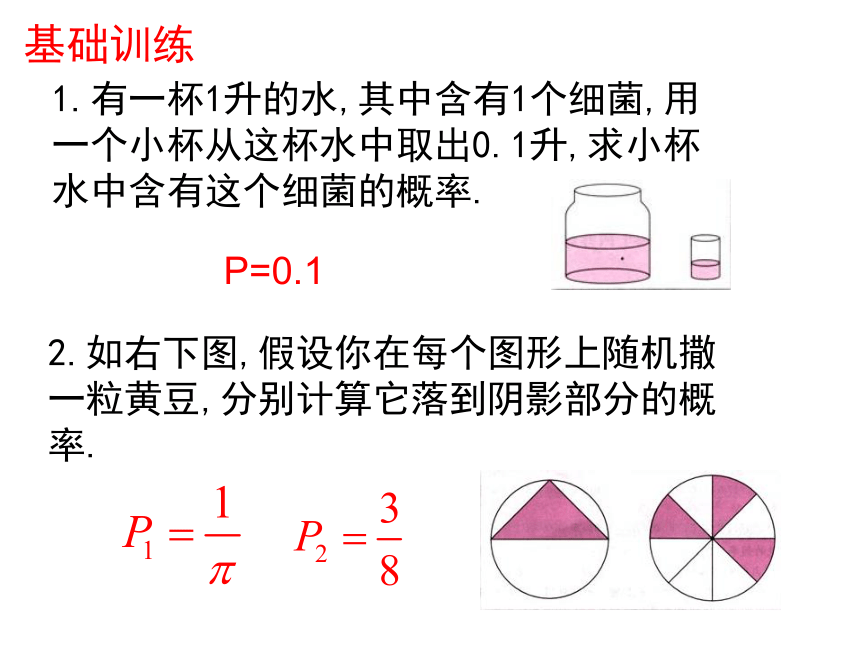
无限多个.(2)每个基本事件出现的可能性相等.在几何概型中,事件A的概率的计算公式:基础训练1.有一杯1升的水,其中含有1个细菌,用
一个小杯从这杯水中取出0.1升,求小杯
水中含有这个细菌的概率.2.如右下图,假设你在每个图形上随机撒
一粒黄豆,分别计算它落到阴影部分的概
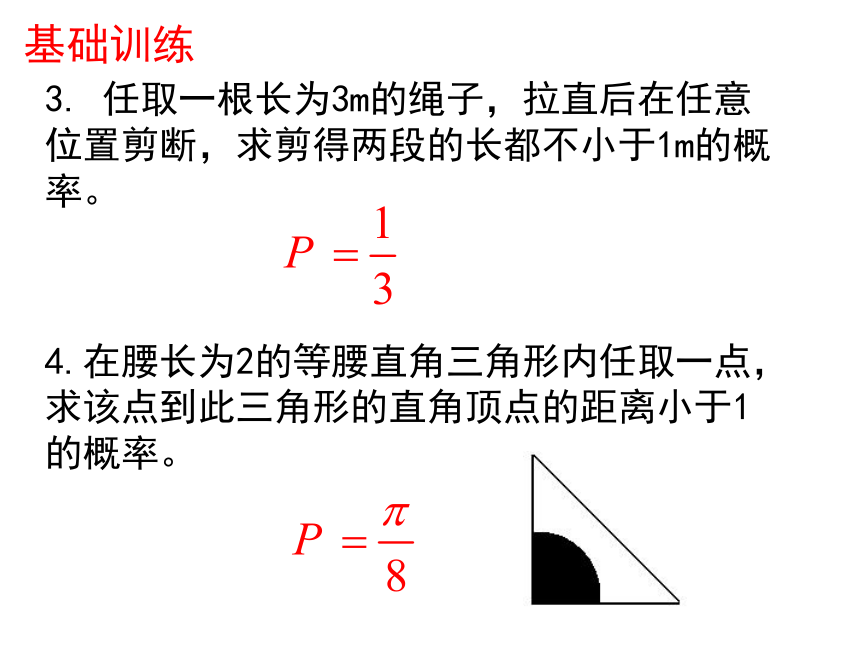
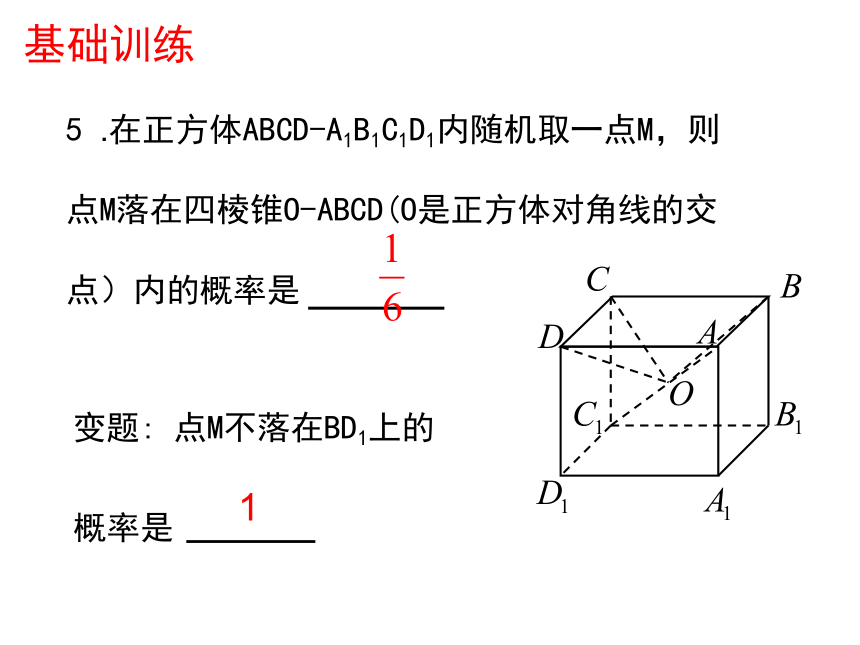
率.P=0.1基础训练3. 任取一根长为3m的绳子，拉直后在任意位置剪断，求剪得两段的长都不小于1m的概率。4.在腰长为2的等腰直角三角形内任取一点，求该点到此三角形的直角顶点的距离小于1的概率。1基础训练例题精讲例1.某公安局用监听录音机记录了两犯罪嫌疑人的谈话，发现30min长的磁带上，从2min处起，有10min长的一段内容包含了两犯罪嫌疑人的信息。后来发现，这段谈话的一部分被某工作人员无意擦掉了，致使从此往后的内容都被擦掉了。那么由于按错键使含有犯罪内容的谈话被部分或全部擦掉的概率有多大？例题精讲例2.甲乙两人约定在6时到7时之间在某处会面,并约定先到者应等候另一个人一刻钟,过时即可离去,求两人能会面的概率.例题精讲例3.将长为2的木棒随机折成3段，求3段能构成三角形的概率.例4.过等腰直角三角形ABC的直角顶点C在角ACB内随机作一条射线,设射线与AB相交于点D,求AD“金币”直径为2r .a 若“金币”成功地落在阶砖上，其圆心必位于右图的绿色区域A内.问题化为:向平面区域S（面积为a2）随机投点（ “金币” 中心），求该点落在区域A内的概率.S于是成功抛中阶砖的概率0<2ra, 你愿意玩这个游戏吗？课堂小结：1.几何概型的特点：无限性、等可能性
2.几何概型的概率公式.
3.几何概型的运用：关键是在实际问题中建立起几何概型的模型。1.用橡皮泥做成一个直径为6cm的小球，假设橡皮泥中混入了一个很小砂粒，求这个砂粒距离球心不小于1cm的概率。巩固练习巩固练习2.(意大利馅饼问题)某馅饼屋中有一个镖靶，该靶为正方形板，边长为18厘米。每个顾客可投一镖并可有机会相应奖品，镖靶中画有三个同心圆，圆心在靶心，若击中半径为1厘米的最内层圆域．可得一个大馅饼；击中半径为1厘米到2厘米之间的环域时，得一个中馅饼；击中半径为2厘米到3厘米之间的环域时，得一个小馅饼，击中靶上的其他部分，则得不到谄饼，假设每个顾客都能投镖中靶，且圆的周边线无宽度，试求一顾客将嬴得：
（a）一张大馅饼，
（b）一张中馅饼，
（c）一张小馅饼，
（d）没得到馅饼的概率