28.2.1解直角三角形 课件(共31张PPT)
文档属性
| 名称 | 28.2.1解直角三角形 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 14.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 12:32:05 | ||
图片预览








文档简介
(共31张PPT)
28.2.1解直角三角形
第二十八章 锐角三角函数
素养目标
1.了解解直角三角形的概念;
2.理解、掌握直角三角形中的五个元素之间的联系;
3.能根据直角三角形中除直角以外的两个元素(至少有一个是边),解直角三角形;
重点
重难点
新课导入
A
C
B
直角三角形中,除直角外,共有5个元素,
即三条边和两个锐角.
直角三角形由哪些元素组成?
【问题1】能否通过直角三角形中的已知元素求出未知元素?
【问题2】需要几个已知元素才能求出其余的所有未知元素?
下面我们带着问题开始本节课的学习探究
探究新知
现在我们回到本章引言中提到的比萨斜塔倾斜程度的问题.
我们能否运用前几节所学的知识解决该问题?
探究新知
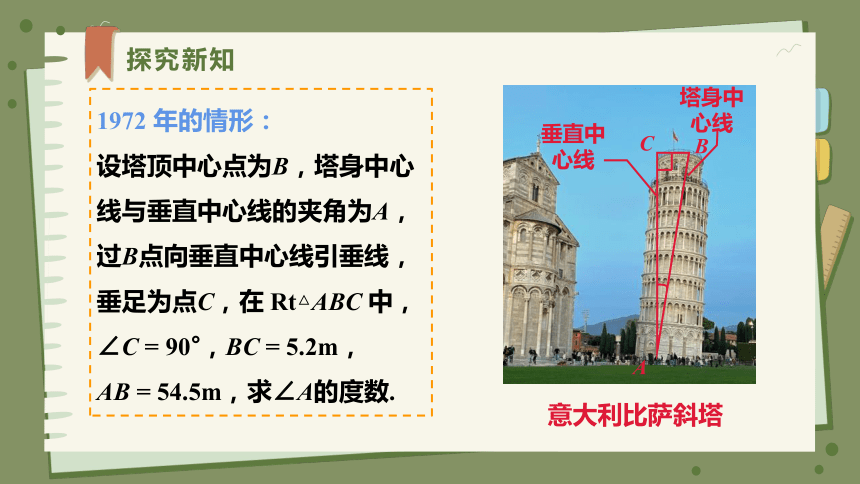
意大利比萨斜塔
垂直中心线
塔身中心线
1972 年的情形:
设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过B点向垂直中心线引垂线,垂足为点C,在 Rt△ABC 中,∠C = 90°,BC = 5.2m,
AB = 54.5m,求∠A的度数.
B
A
C
探究新知
垂直中心线
塔身中心线
B
A
C
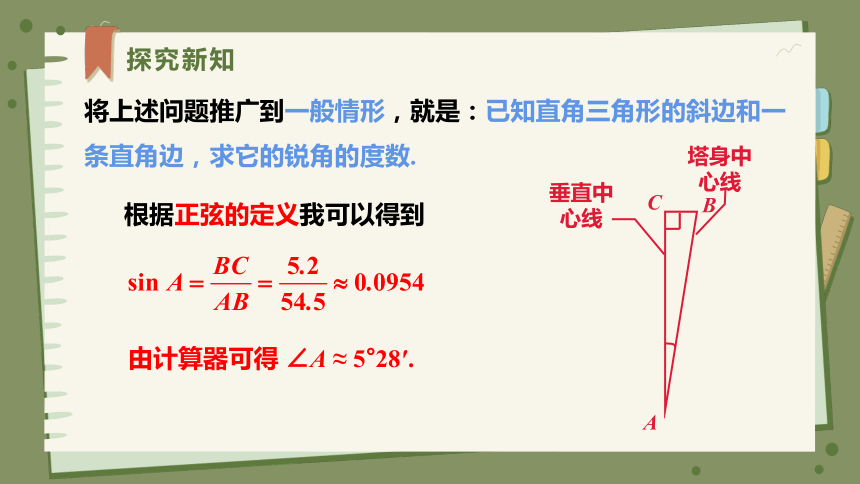
由计算器可得 ∠A ≈ 5°28′.
将上述问题推广到一般情形,就是:已知直角三角形的斜边和一条直角边,求它的锐角的度数.
根据正弦的定义我可以得到
探究新知
思考:在上面的Rt△ABC中,除了能求出∠A 的度数,你能求出其他角或者边吗?
请说出你的思路和依据,不用解答
【总结】一般地,在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角,由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
探究新知
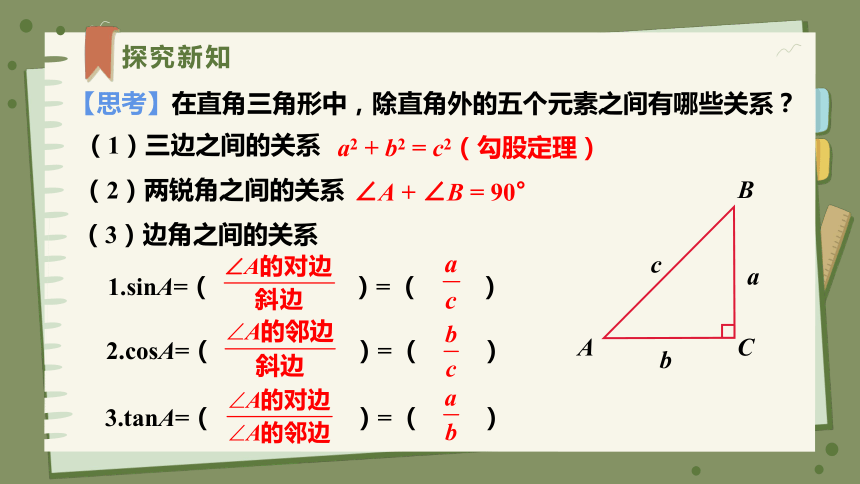
【思考】在直角三角形中,除直角外的五个元素之间有哪些关系?
A
B
C
b
a
c
(1)三边之间的关系
a2 + b2 = c2(勾股定理)
(2)两锐角之间的关系
∠A + ∠B = 90°
(3)边角之间的关系
1.sinA=( )= ( )
2.cosA=( )= ( )
3.tanA=( )= ( )
探究新知
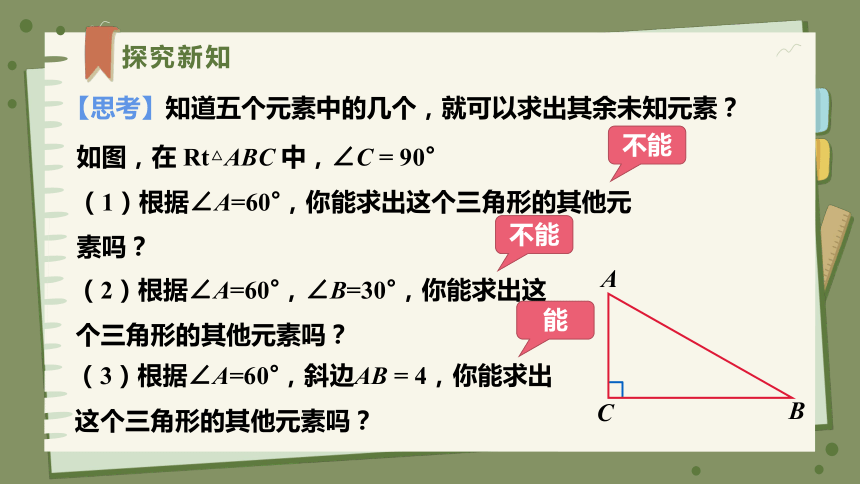
【思考】知道五个元素中的几个,就可以求出其余未知元素?
如图,在 Rt△ABC 中,∠C = 90°
(1)根据∠A=60°,你能求出这个三角形的其他元素吗?
(2)根据∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?
(3)根据∠A=60°,斜边AB = 4,你能求出这个三角形的其他元素吗?
不能
不能
能
A
B
C
探究新知
在 Rt△ABC 中,∠C = 90°,∠A = 60°,斜边AB = 4,你能求出这个三角形的其他元素吗?
60°
A
B
C
已知∠A=60°,因此可以得到
【总结】已知一斜边和一锐角,可以解这个直角三角形.
探究新知
【总结】已知一直角边和一锐角,可以解这个直角三角形.
如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形 (结果保留小数点后一位).
解:
A
B
C
b
c
a
35°
探究新知
A
B
C
如图,在Rt△ABC中,∠C = 90°,AC = , ,
解这个直角三角形.
解:
【总结】已知两直角边,可以解这个直角三角形.
探究新知
如图所示,在Rt△ABC中,∠C=90°,AC=2,AB=4,解这个直角三角形.
A
B
C
【总结】已知一直角边和一斜边,可以解这个直角三角形.
归纳总结
在Rt△ABC中,已知一角或两角,不能求其它元素;已知一角一边或两边,能求其他元素
【总结】在直角三角形中,除直角外的五个元素中,已知其中的两个元素(至少有一个是边),可求出其余的未知元素(知二求三)
解直角三角形的两种基本类型:
①已知一角一边,解直角三角形;
②已知两边,解直角三角形.
锐角
邻边、对边或斜边
两条直角边,或斜边和一条直角边
图形 已知条件 解法
两边 两直角边(a,b)
斜边、一直角边 (如c,a)
一边和一锐角 一直角边和一锐角 一锐角与邻边(如 ∠A,b)
一锐角与对边(如∠A,a )
一锐角与斜边(如 ∠A,c)
A
B
C
b
a
c
B
C
D
9
小结
解直角三角形
解题依据
除直角外五个元素中,知二(至少一边)求三
勾股定理
两锐角互余
锐角三角函数
已知两边
已知一边
一角
两条直角边
一直角边与斜边
一直角边与一角
斜边与一角
谢谢同学们的聆听
28.2.1解直角三角形
第二十八章 锐角三角函数
素养目标
1.了解解直角三角形的概念;
2.理解、掌握直角三角形中的五个元素之间的联系;
3.能根据直角三角形中除直角以外的两个元素(至少有一个是边),解直角三角形;
重点
重难点
新课导入
A
C
B
直角三角形中,除直角外,共有5个元素,
即三条边和两个锐角.
直角三角形由哪些元素组成?
【问题1】能否通过直角三角形中的已知元素求出未知元素?
【问题2】需要几个已知元素才能求出其余的所有未知元素?
下面我们带着问题开始本节课的学习探究
探究新知
现在我们回到本章引言中提到的比萨斜塔倾斜程度的问题.
我们能否运用前几节所学的知识解决该问题?
探究新知
意大利比萨斜塔
垂直中心线
塔身中心线
1972 年的情形:
设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过B点向垂直中心线引垂线,垂足为点C,在 Rt△ABC 中,∠C = 90°,BC = 5.2m,
AB = 54.5m,求∠A的度数.
B
A
C
探究新知
垂直中心线
塔身中心线
B
A
C
由计算器可得 ∠A ≈ 5°28′.
将上述问题推广到一般情形,就是:已知直角三角形的斜边和一条直角边,求它的锐角的度数.
根据正弦的定义我可以得到
探究新知
思考:在上面的Rt△ABC中,除了能求出∠A 的度数,你能求出其他角或者边吗?
请说出你的思路和依据,不用解答
【总结】一般地,在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角,由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
探究新知
【思考】在直角三角形中,除直角外的五个元素之间有哪些关系?
A
B
C
b
a
c
(1)三边之间的关系
a2 + b2 = c2(勾股定理)
(2)两锐角之间的关系
∠A + ∠B = 90°
(3)边角之间的关系
1.sinA=( )= ( )
2.cosA=( )= ( )
3.tanA=( )= ( )
探究新知
【思考】知道五个元素中的几个,就可以求出其余未知元素?
如图,在 Rt△ABC 中,∠C = 90°
(1)根据∠A=60°,你能求出这个三角形的其他元素吗?
(2)根据∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?
(3)根据∠A=60°,斜边AB = 4,你能求出这个三角形的其他元素吗?
不能
不能
能
A
B
C
探究新知
在 Rt△ABC 中,∠C = 90°,∠A = 60°,斜边AB = 4,你能求出这个三角形的其他元素吗?
60°
A
B
C
已知∠A=60°,因此可以得到
【总结】已知一斜边和一锐角,可以解这个直角三角形.
探究新知
【总结】已知一直角边和一锐角,可以解这个直角三角形.
如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形 (结果保留小数点后一位).
解:
A
B
C
b
c
a
35°
探究新知
A
B
C
如图,在Rt△ABC中,∠C = 90°,AC = , ,
解这个直角三角形.
解:
【总结】已知两直角边,可以解这个直角三角形.
探究新知
如图所示,在Rt△ABC中,∠C=90°,AC=2,AB=4,解这个直角三角形.
A
B
C
【总结】已知一直角边和一斜边,可以解这个直角三角形.
归纳总结
在Rt△ABC中,已知一角或两角,不能求其它元素;已知一角一边或两边,能求其他元素
【总结】在直角三角形中,除直角外的五个元素中,已知其中的两个元素(至少有一个是边),可求出其余的未知元素(知二求三)
解直角三角形的两种基本类型:
①已知一角一边,解直角三角形;
②已知两边,解直角三角形.
锐角
邻边、对边或斜边
两条直角边,或斜边和一条直角边
图形 已知条件 解法
两边 两直角边(a,b)
斜边、一直角边 (如c,a)
一边和一锐角 一直角边和一锐角 一锐角与邻边(如 ∠A,b)
一锐角与对边(如∠A,a )
一锐角与斜边(如 ∠A,c)
A
B
C
b
a
c
B
C
D
9
小结
解直角三角形
解题依据
除直角外五个元素中,知二(至少一边)求三
勾股定理
两锐角互余
锐角三角函数
已知两边
已知一边
一角
两条直角边
一直角边与斜边
一直角边与一角
斜边与一角
谢谢同学们的聆听
