电磁学、动力学必备知识点合集
文档属性
| 名称 | 电磁学、动力学必备知识点合集 |  | |
| 格式 | docx | ||
| 文件大小 | 548.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-25 13:30:58 | ||
图片预览


文档简介
电磁学,动力学必背知识点
电场
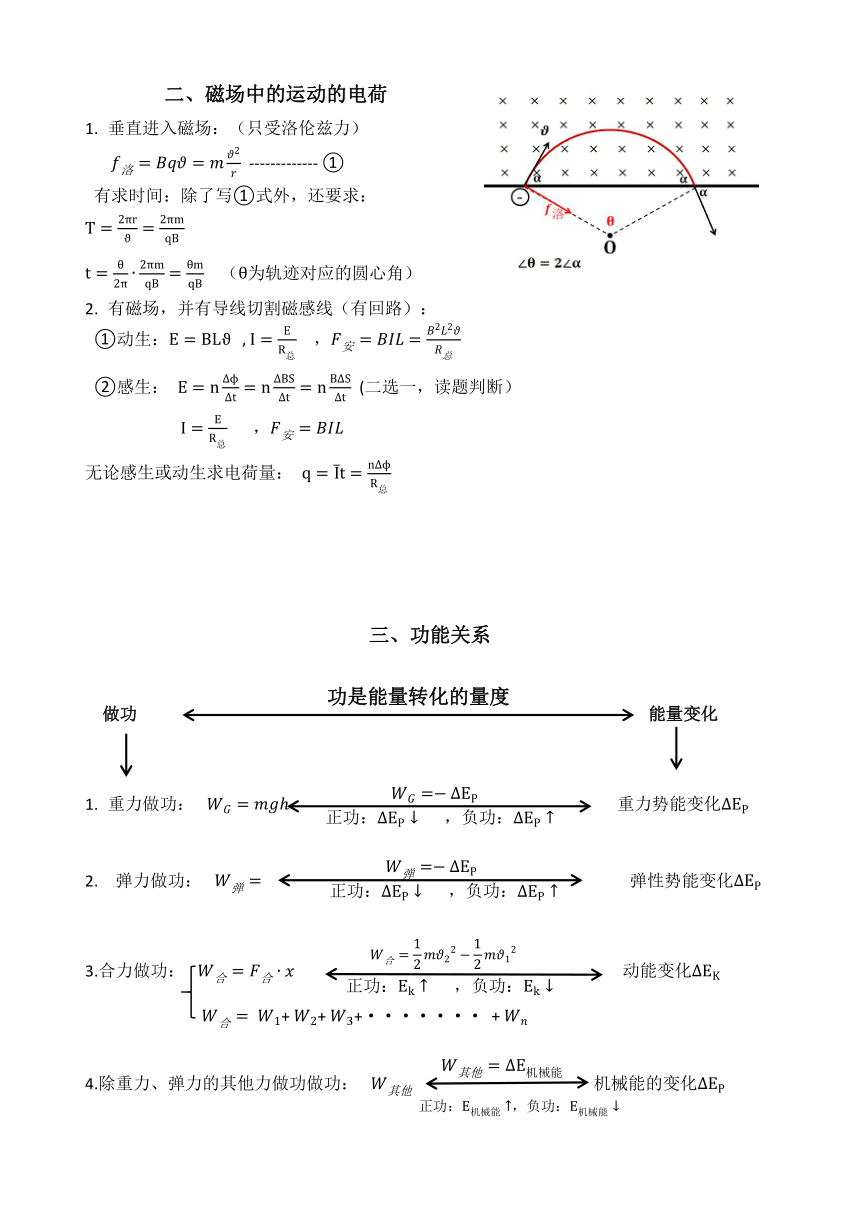
电场强度: (一切电场), (匀强电场) , (真空中点电荷激发的)
电势: (正负代入,正负表示大小),变形
电势差: , (正负代入) ,
U=Ed(匀强),如出现左图所示的情况,那么电势差为
功能关系 :电场力做功等于电势能的变化量。
电场力做正(负)功,电势能减少(增加)
电场力做功的公式:① q(一切电场)
② W=Eqd (匀强电场)
③ 动能定理:
5.电场中的直线加速:
① 求加速后的速度,由动能定理 qU= 得,
② 求时间: 或
③ 加速度:
6.电场中的类平抛运动:(垂直于电场进入电场)
沿极板方向:匀速直线运动
垂直于极板方向:初速度为零的匀加速直线运动
加速度a由静电力提供。
③
-----------------------------④
⑤
---------------------------⑥
由动能定理有: Eqy = -------⑦
磁场中的运动的电荷
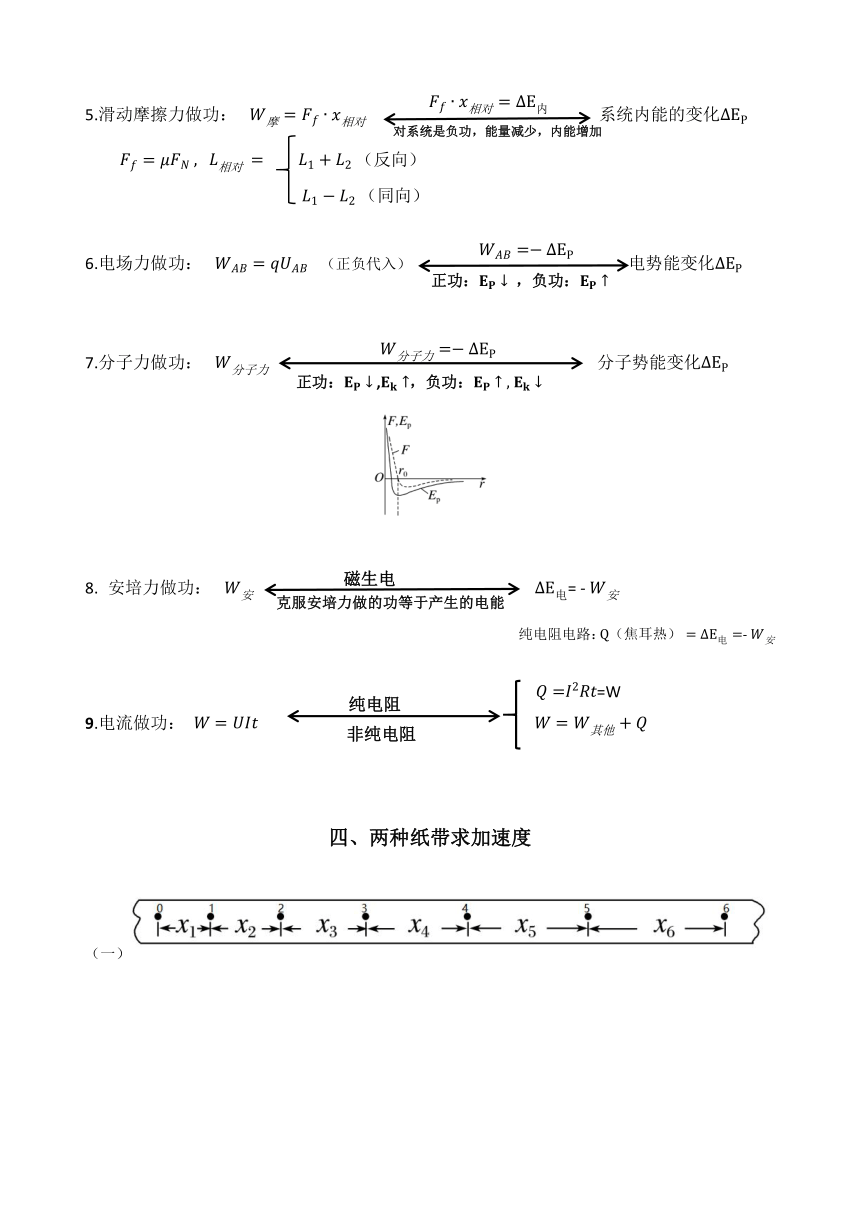
垂直进入磁场:(只受洛伦兹力)
------------- ①
有求时间:除了写①式外,还要求:
(为轨迹对应的圆心角)
有磁场,并有导线切割磁感线(有回路):
①动生: ,
②感生: (二选一,读题判断)
,
无论感生或动生求电荷量:
功能关系
做功 能量变化
重力做功: 重力势能变化
弹力做功: 弹性势能变化
3.合力做功: 动能变化
+++·······
4.除重力、弹力的其他力做功做功: 机械能的变化
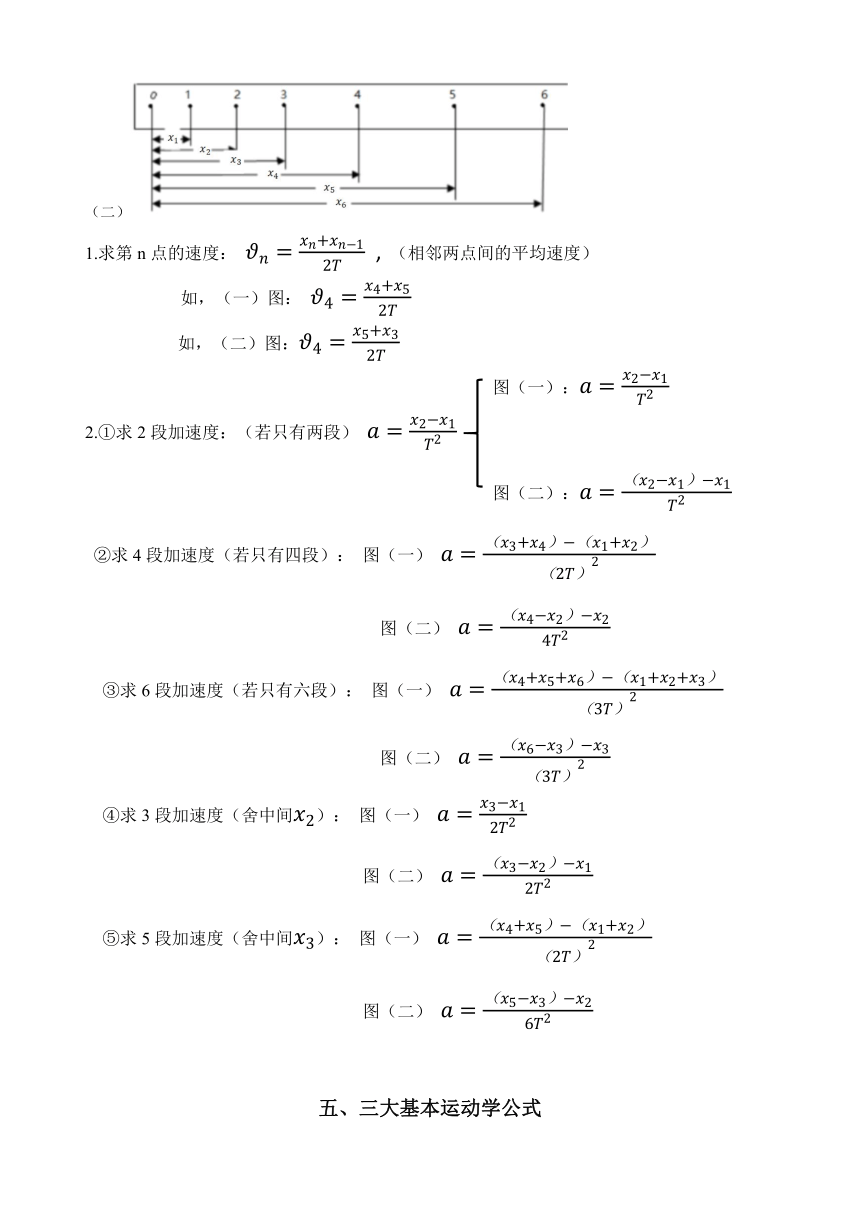
5.滑动摩擦力做功: 系统内能的变化
(反向)
(同向)
6.电场力做功: (正负代入) 电势能变化
7.分子力做功: 分子势能变化
安培力做功: = -
纯电阻电路:-
=W
9.电流做功:
两种纸带求加速度
(二)
1.求第n点的速度: , (相邻两点间的平均速度)
如,(一)图:
如,(二)图:
图(一):
2.①求2段加速度:(若只有两段)
图(二):
②求4段加速度(若只有四段): 图(一)
图(二)
③求6段加速度(若只有六段): 图(一)
图(二)
④求3段加速度(舍中间): 图(一)
图(二)
⑤求5段加速度(舍中间): 图(一)
图(二)
三大基本运动学公式
速度公式:
位移公式:
速度位移公式:
刹车时间: , 刹车位移: ,均代入正值。
推论: ①
匀变速:②连续相等的相邻时间间隔T内的位移差:Δx=aT2. (如,Δx=x2-x1 )
Δx=2-1 =3-2 =4-3 =5-4 =........................=n-n-1 =aT2
不连续相等的时间的位移差:xm-xn=(m-n)aT2
比例式:①连续相等时间的位移之比:
(,匀变速)1=2=3=............=n= 1 : 3 : 5 : ....................... : (2n-1)
②1T内,2T内,3T内................nT内的位移之比:
(), 1 : 2 : 3 : ............: n = 12 : 22 : 32 : ....................... : n2
③1内,2内,3内................n内的时间之比:
(), t1 : t2 : t3 : ............: tn = 1 :: : ....................... :
④第一个,第二个,第三个,................ 第n个的时间之比:
t1:t2:t3 : ........: tn = 1:( ): ( ): .......: ( )
⑤1T末,2T末,3T末........nT末的速度之比:
(), : : : ............: = 1 : 2 : 3 : ....................... : n
⑥ 1末,2末,3末.........n末的速度之比:
(), : : : ............: = 1 : : : ....................... :
六、自由落体运动和平抛运动
1.自由落体运动:,= ,
1)
2) 下落时间: (常用)
3): 落地速度:
4) 方向相同
5)图像:
6)推论: , 仍适用,比例式也仍使用
2.竖直上抛运动:,= ,
1)处理题的方法: ①全程法:向上的匀减速直线运动
②分段法:向上的匀减速直线运动,向下的自由落体运动
2)全程公式: ①
② 应用时注意所有量的方向(正负代入)
③
二级公式: ①最大高度 :
②上升时间:
③全程时间: (对称性)
t图像:
斜率: k=-
t > : 即开始下落, 为负值
t > 时落到抛出点以下,h为负值
万有引力与航天
开普勒三定律: ① 轨道定律:太阳是椭圆轨道的焦点上
②面积定律:近地点速度大于远地点速度
③周期定律: =k ,与中心天体有关(质量M)
万有引力与重力:(自转影响,重力为万有引力的分力)
①赤道:
②两极: ,纬度越高,值越大,两极最大,赤道最小
重力加速度: ①地表:
②距地表h高度处:
或
天体质量M合密度的计算方法:
- R法: ;
(利用环绕天体)(r:轨道半径) 万有引力充当向心力
T-r 法: M ; (若为近地卫星r=R
r 法: ,由
r 法: ,由 知求必须要已知R
法: ,由 ,由 (R为天体半径)
卫星运行的参量与轨道半径变化的规律:万有引力充当向心力
G=
同步卫星:定轨、定高、定速、定周期
(赤道平面)(3.6x107 mm)(、定)(24h)
同步卫星2,近地卫星1,赤道上物体3比较:
2,3相当于同轴转动
m3=mR 自传向心力(小于万有引力)
8.第一宇宙速度的求法:(即求近地卫星速度)最小发射速度,最大环绕速度
方法一(r=R)、 ①
方法二、 ② 或①②两式联立得
= ③
9.三大宇宙速度:7.9 km/s , 11.2 km/s 16.7 km/s
卫星发射速度 ① 脱离地球束缚,变成太阳的卫星
② 脱离太阳的束缚,飞出太阳系
③ 绕地球椭圆轨道运动
④ 绕太阳椭圆轨道运动
⑤ 飞出太阳系
10.卫星变轨,对接问题:(加速升轨,减速降轨)
1)变轨:如图:“三次加速升轨” 至3轨道
1,3是圆形轨道,2是椭圆轨道
①在1轨道P点加速进入2轨道:
在2轨道Q点加速进入3轨道:
轨2:P是近地点,Q是远地点:
所以 并 (因为)
②
③ , , ,所以=
④ , ,
⑤ 加速升轨: 有外力做正功,机械能增加
机械能:
2)减速至较低轨道,再加速追上空间站完成对接。
11.某星瓦解临界条件:(即万有引力提供自传向心力,物体对星体无压力)
或
12.双星模型:(相当于同轴转动)
,相互引力充当向心力
①
②
又= ,①②变形后 : ③ ; ④
得: 质量与半径成反比,>
又得 线速度与半径成正比 >
③+④得: (M为双星总质量)
得
13.三星模型: 1,2,3三颗质量均为m得卫星绕其中心O,做圆周运动,每颗星受其他两颗星的引力合为: ,又
由牛顿第二定律:
m =
m
14.四星模型: 1,2,3,4颗质量均为m
每颗星受其他三颗星的引力合为:
由牛顿第二定律:=
m
m
得: , ,
15.追及、相遇问题:
1)
圈数:
3)相距最远: ①
②
4)共线次数n: ①
②
电场
电场强度: (一切电场), (匀强电场) , (真空中点电荷激发的)
电势: (正负代入,正负表示大小),变形
电势差: , (正负代入) ,
U=Ed(匀强),如出现左图所示的情况,那么电势差为
功能关系 :电场力做功等于电势能的变化量。
电场力做正(负)功,电势能减少(增加)
电场力做功的公式:① q(一切电场)
② W=Eqd (匀强电场)
③ 动能定理:
5.电场中的直线加速:
① 求加速后的速度,由动能定理 qU= 得,
② 求时间: 或
③ 加速度:
6.电场中的类平抛运动:(垂直于电场进入电场)
沿极板方向:匀速直线运动
垂直于极板方向:初速度为零的匀加速直线运动
加速度a由静电力提供。
③
-----------------------------④
⑤
---------------------------⑥
由动能定理有: Eqy = -------⑦
磁场中的运动的电荷
垂直进入磁场:(只受洛伦兹力)
------------- ①
有求时间:除了写①式外,还要求:
(为轨迹对应的圆心角)
有磁场,并有导线切割磁感线(有回路):
①动生: ,
②感生: (二选一,读题判断)
,
无论感生或动生求电荷量:
功能关系
做功 能量变化
重力做功: 重力势能变化
弹力做功: 弹性势能变化
3.合力做功: 动能变化
+++·······
4.除重力、弹力的其他力做功做功: 机械能的变化
5.滑动摩擦力做功: 系统内能的变化
(反向)
(同向)
6.电场力做功: (正负代入) 电势能变化
7.分子力做功: 分子势能变化
安培力做功: = -
纯电阻电路:-
=W
9.电流做功:
两种纸带求加速度
(二)
1.求第n点的速度: , (相邻两点间的平均速度)
如,(一)图:
如,(二)图:
图(一):
2.①求2段加速度:(若只有两段)
图(二):
②求4段加速度(若只有四段): 图(一)
图(二)
③求6段加速度(若只有六段): 图(一)
图(二)
④求3段加速度(舍中间): 图(一)
图(二)
⑤求5段加速度(舍中间): 图(一)
图(二)
三大基本运动学公式
速度公式:
位移公式:
速度位移公式:
刹车时间: , 刹车位移: ,均代入正值。
推论: ①
匀变速:②连续相等的相邻时间间隔T内的位移差:Δx=aT2. (如,Δx=x2-x1 )
Δx=2-1 =3-2 =4-3 =5-4 =........................=n-n-1 =aT2
不连续相等的时间的位移差:xm-xn=(m-n)aT2
比例式:①连续相等时间的位移之比:
(,匀变速)1=2=3=............=n= 1 : 3 : 5 : ....................... : (2n-1)
②1T内,2T内,3T内................nT内的位移之比:
(), 1 : 2 : 3 : ............: n = 12 : 22 : 32 : ....................... : n2
③1内,2内,3内................n内的时间之比:
(), t1 : t2 : t3 : ............: tn = 1 :: : ....................... :
④第一个,第二个,第三个,................ 第n个的时间之比:
t1:t2:t3 : ........: tn = 1:( ): ( ): .......: ( )
⑤1T末,2T末,3T末........nT末的速度之比:
(), : : : ............: = 1 : 2 : 3 : ....................... : n
⑥ 1末,2末,3末.........n末的速度之比:
(), : : : ............: = 1 : : : ....................... :
六、自由落体运动和平抛运动
1.自由落体运动:,= ,
1)
2) 下落时间: (常用)
3): 落地速度:
4) 方向相同
5)图像:
6)推论: , 仍适用,比例式也仍使用
2.竖直上抛运动:,= ,
1)处理题的方法: ①全程法:向上的匀减速直线运动
②分段法:向上的匀减速直线运动,向下的自由落体运动
2)全程公式: ①
② 应用时注意所有量的方向(正负代入)
③
二级公式: ①最大高度 :
②上升时间:
③全程时间: (对称性)
t图像:
斜率: k=-
t > : 即开始下落, 为负值
t > 时落到抛出点以下,h为负值
万有引力与航天
开普勒三定律: ① 轨道定律:太阳是椭圆轨道的焦点上
②面积定律:近地点速度大于远地点速度
③周期定律: =k ,与中心天体有关(质量M)
万有引力与重力:(自转影响,重力为万有引力的分力)
①赤道:
②两极: ,纬度越高,值越大,两极最大,赤道最小
重力加速度: ①地表:
②距地表h高度处:
或
天体质量M合密度的计算方法:
- R法: ;
(利用环绕天体)(r:轨道半径) 万有引力充当向心力
T-r 法: M ; (若为近地卫星r=R
r 法: ,由
r 法: ,由 知求必须要已知R
法: ,由 ,由 (R为天体半径)
卫星运行的参量与轨道半径变化的规律:万有引力充当向心力
G=
同步卫星:定轨、定高、定速、定周期
(赤道平面)(3.6x107 mm)(、定)(24h)
同步卫星2,近地卫星1,赤道上物体3比较:
2,3相当于同轴转动
m3=mR 自传向心力(小于万有引力)
8.第一宇宙速度的求法:(即求近地卫星速度)最小发射速度,最大环绕速度
方法一(r=R)、 ①
方法二、 ② 或①②两式联立得
= ③
9.三大宇宙速度:7.9 km/s , 11.2 km/s 16.7 km/s
卫星发射速度 ① 脱离地球束缚,变成太阳的卫星
② 脱离太阳的束缚,飞出太阳系
③ 绕地球椭圆轨道运动
④ 绕太阳椭圆轨道运动
⑤ 飞出太阳系
10.卫星变轨,对接问题:(加速升轨,减速降轨)
1)变轨:如图:“三次加速升轨” 至3轨道
1,3是圆形轨道,2是椭圆轨道
①在1轨道P点加速进入2轨道:
在2轨道Q点加速进入3轨道:
轨2:P是近地点,Q是远地点:
所以 并 (因为)
②
③ , , ,所以=
④ , ,
⑤ 加速升轨: 有外力做正功,机械能增加
机械能:
2)减速至较低轨道,再加速追上空间站完成对接。
11.某星瓦解临界条件:(即万有引力提供自传向心力,物体对星体无压力)
或
12.双星模型:(相当于同轴转动)
,相互引力充当向心力
①
②
又= ,①②变形后 : ③ ; ④
得: 质量与半径成反比,>
又得 线速度与半径成正比 >
③+④得: (M为双星总质量)
得
13.三星模型: 1,2,3三颗质量均为m得卫星绕其中心O,做圆周运动,每颗星受其他两颗星的引力合为: ,又
由牛顿第二定律:
m =
m
14.四星模型: 1,2,3,4颗质量均为m
每颗星受其他三颗星的引力合为:
由牛顿第二定律:=
m
m
得: , ,
15.追及、相遇问题:
1)
圈数:
3)相距最远: ①
②
4)共线次数n: ①
②
同课章节目录
