用函数模型解决实际问题
图片预览





文档简介
课件15张PPT。4.2.2用函数模型解决实际问题
在教科书第三章的章头图中,有一大群喝水、嬉戏的兔子,但是这群兔子曾使澳大利亚伤透了脑筋.1859年,有人从欧洲带进澳洲几只兔子,由于澳洲有茂盛的牧草,而且没有兔子的天敌,兔子数量不断增加,不到100年,兔子们占领了整个澳大利亚,数量达到75亿只.可爱的兔子变得可恶起来,75亿只兔子吃掉了相当于75亿只羊所吃的牧草,草原的载畜率大大降低,而牛羊是澳大利亚的主要牲口.这使澳大利亚头痛不已,他们采用各种方法消灭这些兔子,直至二十世纪五十年代,科学家采用载液瘤病毒杀死了百分之九十的野兔,澳大利亚人才算松了一口气. 材料:澳大利亚兔子数“爆炸”例1 、 假设你有一笔资金用于投资,现在有三种投资方案供你选择,这三种方案的回报如下:
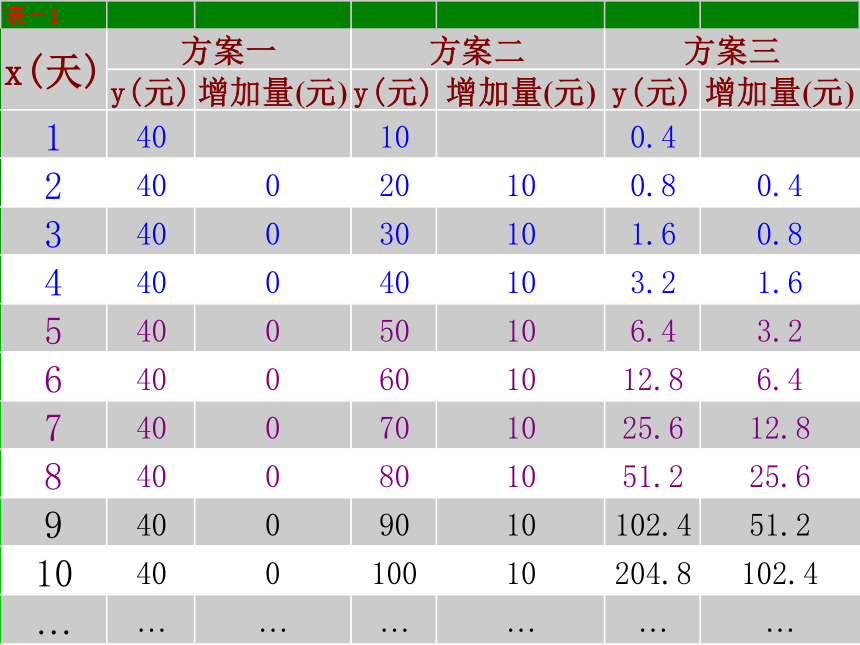
方案一、每天回报40元;
方案二、第一天回报10元,以后每天比前一天多回报10元;
方案三、第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?下面我们先来看两个具体问题。例1、假设你有一笔资金用于投资,现在有三种投资方案供你选择,这三种方案的回报如下:
方案一、每天回报40元;
方案二、第一天回报10元,以后每天比前一天多回报10元;
方案三、第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?分析:2、如何建立日回报效益与天数的函数模型?1、依据什么标准来选取投资方案?日回报效益,还是累计回报效益?分析:2、如何建立日回报效益与天数的函数模型?1、依据什么标准来选取投资方案?日回报效益,还是累计回报效益?解:设第x天所得回报是y元
方案一可以用函数 进行描述;
方案二可以用函数 进行描述;
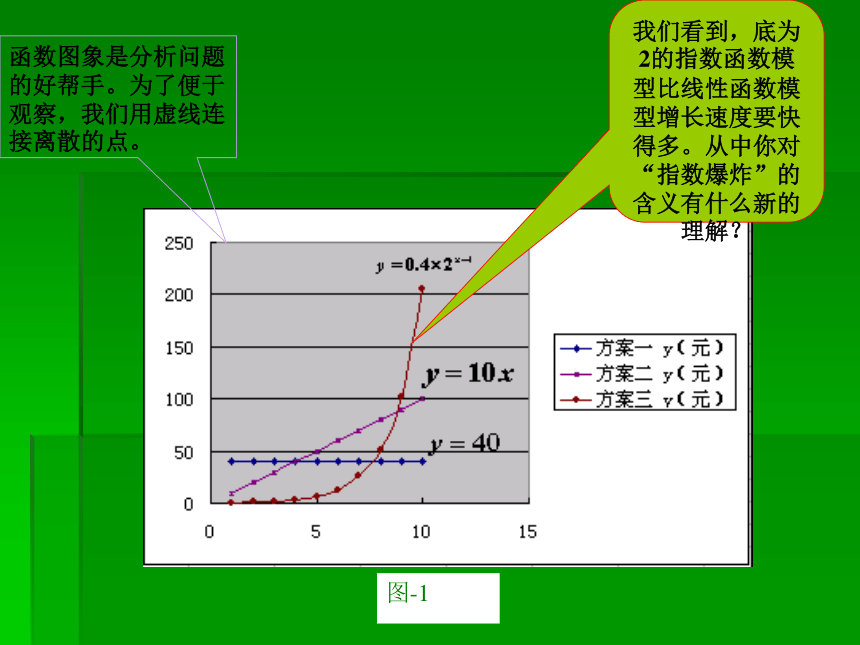
方案三可以用函数 进行描述.3、三个函数模型的增减性如何?4、要对三个方案作出选择,就要对它们的增长情况进行分析,如何分析?我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。从中你对“指数爆炸”的含义有什么新的理解?函数图象是分析问题的好帮手。为了便于观察,我们用虚线连接离散的点。根据以上的分析,是否应作这样的选择:投资5天以下先方案一,投资5~8天先方案二,投资8天以上先方案三? 由表-1和图-1可知,方案一的函数是常数函数,方案二、方案三的函数都是增函数,但是方案三的函数与方案二的函数的增长情况很不同。可以看到,尽管方案一、方案二在第1天所得回报分别是方案三的100倍和25倍,但它们的增长量是成倍增加的,从第7天开始,方案三比其他两个方案增长得快得多,这种增长速度是方案一、方案二所 无法企及的,从每天所得回报看,在第1~4天,方案一最多,在5~8天,方案二最多;第9天开始 ,方案三比其他两个方案所得回报多得多,到第30天,所得回报已超过2亿元。 因此,投资8天以下(不含8天),应选择第一种投资方案;投资8~10天,应选择第二种投资方案;投资11天(含11 天)以上,刚应选择第三种投资方案。例2、 电声器材厂在生产扬声器过程中,有一道重要的工序:使用胶水粘合标准,经常出现胶水过多,往外溢;过少,产生脱胶,扬声器中的磁钢和夹板。长期以来,由于对胶水的用量没有一个准确的影响了产品的质量。
经过实验,有了一些恰当用胶水量的集体数据:?XY50 100 150 200 250 300 350 400 450 50013246578从图中可知:这些点基本分布在一条直线上。
所以,可以用函数 y=ax+b 表示用胶量与磁钢面积的关系。
取点(56.6 ,0.812),(189.0 ,2.86)代入:
得:a=0.01547 , b= -0.06350即:y=0.01547 x -0.06350课堂小结:
本节课主要学习了函数模型的实例应用,主要是一次函数模型,通过建立模型,利用函数图像性质性质对解析式进行处理得出数学结论,并根据数学结论解决实际问题.函数思想:
通过一些数据寻求事物规律,往往是通过绘出这些数据在指教坐标系中的点,观察这些点的特征,看它们接近我们熟悉的哪一种函数图像,即选定函数形式,将一些数据代入,求出具体的函数表达式,再做必要的检验,基本符合实际,就确定。
我们称这种方法为— —数据拟合。作业
P130 习题4-2 A组 1
B组 1课堂练习 某中学的研究性学习小组为考察闽江口的一个小岛的湿地开发情况,从某码头乘汽艇出发,沿直线方向匀速开往该岛,靠近岛时,绕小岛环行两周后,把汽艇靠岸,上岛考察,然后乘汽艇沿远航线提速返回,t为出发后的某一时刻,S为汽艇与码头在时刻t下的距离,下列图像中大致能表示S=f(t)的函数关系的是( )
在教科书第三章的章头图中,有一大群喝水、嬉戏的兔子,但是这群兔子曾使澳大利亚伤透了脑筋.1859年,有人从欧洲带进澳洲几只兔子,由于澳洲有茂盛的牧草,而且没有兔子的天敌,兔子数量不断增加,不到100年,兔子们占领了整个澳大利亚,数量达到75亿只.可爱的兔子变得可恶起来,75亿只兔子吃掉了相当于75亿只羊所吃的牧草,草原的载畜率大大降低,而牛羊是澳大利亚的主要牲口.这使澳大利亚头痛不已,他们采用各种方法消灭这些兔子,直至二十世纪五十年代,科学家采用载液瘤病毒杀死了百分之九十的野兔,澳大利亚人才算松了一口气. 材料:澳大利亚兔子数“爆炸”例1 、 假设你有一笔资金用于投资,现在有三种投资方案供你选择,这三种方案的回报如下:
方案一、每天回报40元;
方案二、第一天回报10元,以后每天比前一天多回报10元;
方案三、第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?下面我们先来看两个具体问题。例1、假设你有一笔资金用于投资,现在有三种投资方案供你选择,这三种方案的回报如下:
方案一、每天回报40元;
方案二、第一天回报10元,以后每天比前一天多回报10元;
方案三、第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?分析:2、如何建立日回报效益与天数的函数模型?1、依据什么标准来选取投资方案?日回报效益,还是累计回报效益?分析:2、如何建立日回报效益与天数的函数模型?1、依据什么标准来选取投资方案?日回报效益,还是累计回报效益?解:设第x天所得回报是y元
方案一可以用函数 进行描述;
方案二可以用函数 进行描述;
方案三可以用函数 进行描述.3、三个函数模型的增减性如何?4、要对三个方案作出选择,就要对它们的增长情况进行分析,如何分析?我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。从中你对“指数爆炸”的含义有什么新的理解?函数图象是分析问题的好帮手。为了便于观察,我们用虚线连接离散的点。根据以上的分析,是否应作这样的选择:投资5天以下先方案一,投资5~8天先方案二,投资8天以上先方案三? 由表-1和图-1可知,方案一的函数是常数函数,方案二、方案三的函数都是增函数,但是方案三的函数与方案二的函数的增长情况很不同。可以看到,尽管方案一、方案二在第1天所得回报分别是方案三的100倍和25倍,但它们的增长量是成倍增加的,从第7天开始,方案三比其他两个方案增长得快得多,这种增长速度是方案一、方案二所 无法企及的,从每天所得回报看,在第1~4天,方案一最多,在5~8天,方案二最多;第9天开始 ,方案三比其他两个方案所得回报多得多,到第30天,所得回报已超过2亿元。 因此,投资8天以下(不含8天),应选择第一种投资方案;投资8~10天,应选择第二种投资方案;投资11天(含11 天)以上,刚应选择第三种投资方案。例2、 电声器材厂在生产扬声器过程中,有一道重要的工序:使用胶水粘合标准,经常出现胶水过多,往外溢;过少,产生脱胶,扬声器中的磁钢和夹板。长期以来,由于对胶水的用量没有一个准确的影响了产品的质量。
经过实验,有了一些恰当用胶水量的集体数据:?XY50 100 150 200 250 300 350 400 450 50013246578从图中可知:这些点基本分布在一条直线上。
所以,可以用函数 y=ax+b 表示用胶量与磁钢面积的关系。
取点(56.6 ,0.812),(189.0 ,2.86)代入:
得:a=0.01547 , b= -0.06350即:y=0.01547 x -0.06350课堂小结:
本节课主要学习了函数模型的实例应用,主要是一次函数模型,通过建立模型,利用函数图像性质性质对解析式进行处理得出数学结论,并根据数学结论解决实际问题.函数思想:
通过一些数据寻求事物规律,往往是通过绘出这些数据在指教坐标系中的点,观察这些点的特征,看它们接近我们熟悉的哪一种函数图像,即选定函数形式,将一些数据代入,求出具体的函数表达式,再做必要的检验,基本符合实际,就确定。
我们称这种方法为— —数据拟合。作业
P130 习题4-2 A组 1
B组 1课堂练习 某中学的研究性学习小组为考察闽江口的一个小岛的湿地开发情况,从某码头乘汽艇出发,沿直线方向匀速开往该岛,靠近岛时,绕小岛环行两周后,把汽艇靠岸,上岛考察,然后乘汽艇沿远航线提速返回,t为出发后的某一时刻,S为汽艇与码头在时刻t下的距离,下列图像中大致能表示S=f(t)的函数关系的是( )
