26.1.2 反比例函数的图象和性质 课时作业(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质 课时作业(含答案) 2024-2025学年数学人教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 181.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 00:00:00 | ||
图片预览



文档简介
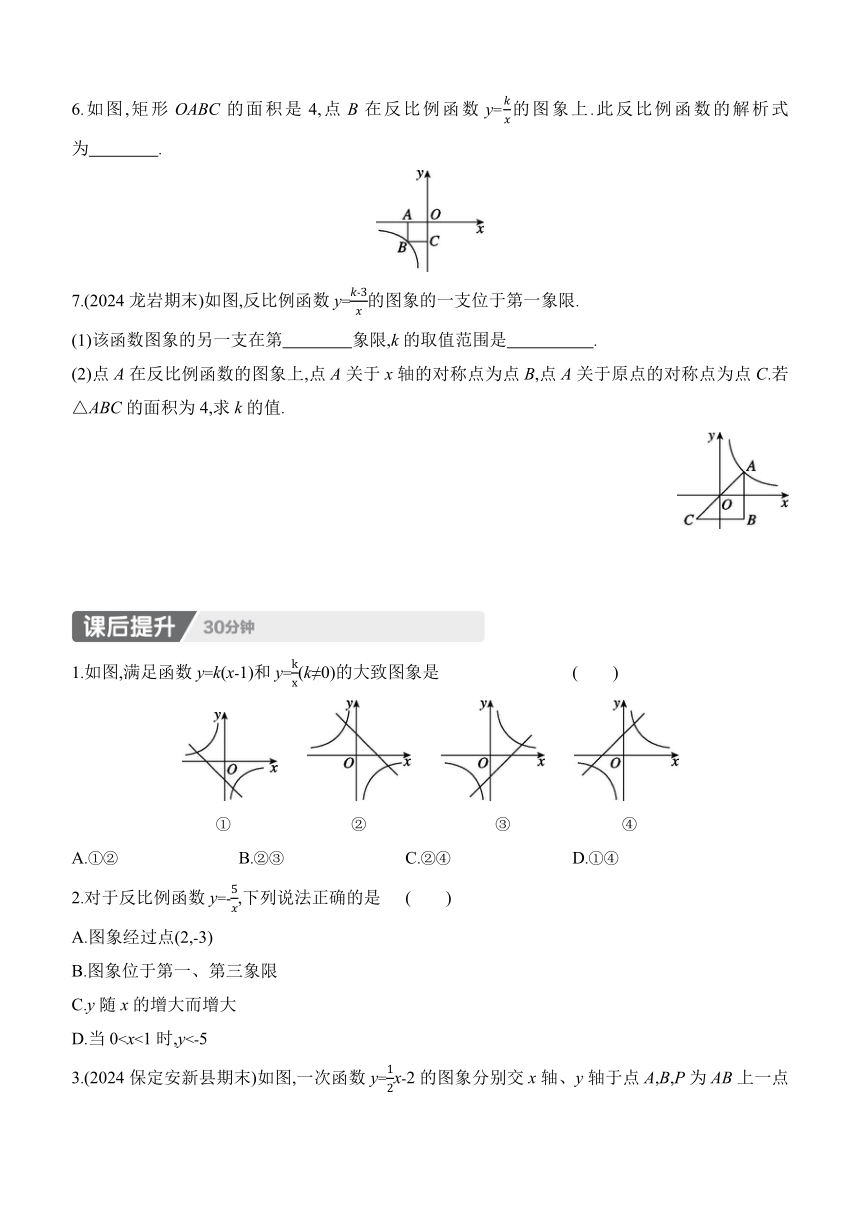
26.1.2 反比例函数的图象和性质
反比例函数的图象
1.反比例函数y=-的图象大致是 ( )
A. B. C. D.
2.如果反比例函数的图象经过点(-3,-4),那么函数的图象在第 象限.
反比例函数的性质
3.(2024唐山滦南县期末)已知反比例函数y=.下列说法正确的是 ( )
A.图象经过点(-3,1)
B.y随x的增大而减小
C.图象不可能和x轴相交
D.图象是轴对称图形但不是中心对称图形
用待定系数法求反比例函数解析式
4.如图,反比例函数y=的图象经过点A(2,1),该反比例函数的解析式为 ( )
A.y= B.y=- C.y= D.y=-
反比例函数y=的几何意义
5.反比例函数y=(x<0)的图象如图所示,AB∥y轴,若△ABC的面积为3,则k的值为 ( )
A. B.- C.3 D.-6
6.如图,矩形OABC的面积是4,点B在反比例函数y=的图象上.此反比例函数的解析式为 .
7.(2024龙岩期末)如图,反比例函数y=的图象的一支位于第一象限.
(1)该函数图象的另一支在第 象限,k的取值范围是 .
(2)点A在反比例函数的图象上,点A关于x轴的对称点为点B,点A关于原点的对称点为点C.若△ABC的面积为4,求k的值.
1.如图,满足函数y=k(x-1)和y=(k≠0)的大致图象是 ( )
① ② ③ ④
A.①② B.②③ C.②④ D.①④
2.对于反比例函数y=-,下列说法正确的是 ( )
A.图象经过点(2,-3)
B.图象位于第一、第三象限
C.y随x的增大而增大
D.当03.(2024保定安新县期末)如图,一次函数y=x-2的图象分别交x轴、y轴于点A,B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=(k>0)的图象于点Q,S△OQC=,则k的值是 ;点Q的坐标为 .
4.如图,在平面直角坐标系中,△AOB的边OB在y轴上,边AB与x轴交于点D,且BD=AD,反比例函数y=(x>0)的图象经过点A.若S△OAB=1,则反比例函数的解析式为 .
5.如图,在△ABC中,AC=BC=5,AB=8,AB⊥x轴,垂足为A,反比例函数y=(x>0)的图象经过点C,交AB于点D.
(1)若OA=AB,求k的值.
(2)若BC=BD,连接OC,求△OAC的面积.
6.(几何直观)如图,过原点O的直线与反比例函数y1=(k≠0)的图象交于A(1,2),B两点,一次函数y2=mx+b(m≠0)的图象过点A与反比例函数交于另一点C(2,n).
(1)求反比例函数的解析式;当y1>y2时,根据图象直接写出x的取值范围.
(2)在y轴上是否存在点M,使得△COM为等腰三角形 若存在,求出点M的坐标;若不存在,请说明理由.
【详解答案】
课堂达标
1.B 解析:在反比例函数y=-中,k=-6<0,图象在第二、第四象限.故选B.
2.一、第三 解析:设反比例函数的解析式为y=(k≠0).∵反比例函数的图象经过点(-3,-4),∴k=(-3)×(-4)=12.
∴函数的图象在第一、第三象限.
3.C 解析:A.∵(-3)×1=-3≠3,∴图象不经过点(-3,1).原说法错误,不符合题意;B.∵k=3>0,∴函数图象的两个分支分别位于第一、第三象限.在每一象限内,y随x的增大而减小.原说法错误,不符合题意;C.∵函数y=是反比例函数,∴图象不可能和x轴相交.原说法正确,符合题意;D.∵函数y=是反比例函数,∴图象是中心对称图形.原说法错误,不符合题意.故选C.
4.C 解析:∵反比例函数y=的图象经过点A(2,1),∴1=.∴k=2.∴该反比例函数的解析式为y=.故选C.
5.D 解析:如图,连接OA.∵AB∥y轴,∴△ABC的面积=△OAB的面积.∵2S△OAB=2×3=6,∴|k|=6.∵反比例函数图象在第二象限,∴k=-6.故选D.
6.y= 解析:设BC=a,AB=b,则点B的坐标为(-a,-b),AB·BC=ab=4.将点B(-a,-b)代入y=中,得k=xy=(-a)×(-b)=ab=4.∴反比例函数的解析式为y=.
7.解:(1)三 k>3
(2)由题意,设点A的坐标为(a,b).
∵点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,点C与点A关于原点O对称,
∴a>0,b>0,点B的坐标是(a,-b),点C的坐标是(-a,-b).
∴BC=a-(-a)=2a,AB=b-(-b)=2b.
∵△ABC的面积为4,∴×AB×BC=4.
∴×2a×2b=4.∴ab=2.
∵点A在反比例函数y=位于第一象限的图象上,
∴k-3=ab=2.解得k=5.
课后提升
1.B 解析:∵y=k(x-1),∴函数y=k(x-1)图象过点(1,0).故①④不符合题意;当k>0时,函数y=k(x-1)过第一、第三、第四象限,函数y=(k≠0)在第一、第三象限;当k<0时,函数y=k(x-1)过第一、第二、第四象限,函数y=(k≠0)在第二、第四象限.故②③符合题意.故选B.
2.D 解析:反比例函数y=-.A.当x=2时,y=-,图象经过点2,-,故选项A不符合题意;B.∵k=-5<0,故该函数图象位于第二、第四象限,故选项B不符合题意;C.在每个象限内,y随x的增大而增大,故选项C不符合题意;D.∵当x=1时,y=-5,x>0时,y<0,∴当03.3 解析:当y=0时,x-2=0,解得x=4.则点A(4,0).∵PC为△AOB的中位线,∴PC∥OB,点C(2,0).∵S△OQC=|k|=,而k>0,∴k=3.∴反比例函数的解析式为y=.当x=2时,y=,∴点Q的坐标为.
4.y= 解析:如图,过点A作x轴的垂线与x轴交于点C.
设点A(a,b),则AC=b,OC=a,AC∥OB.∴∠ACD=∠BOD=90°,∠ADC=∠BDO.∵AD=BD,∴△ADC≌△BDO(AAS).∴S△ADC=S△BDO.∴S△OAC=S△AOD+S△ADC=S△AOD+S△BDO=S△OAB=1.∴×OC×AC=ab=1.∴ab=2,∵点A(a,b)在y=上,∴k=ab=2.∴反比例函数的解析式为y=.
5.解:(1)如图,过点C作CE⊥AB于点E,CF⊥OA于点F,∴四边形AECF为矩形.
∴CF=AE,CE=AF.
∵AB=8,AC=BC=5,CE⊥AB,
∴BE=AE=CF=4.
∴AF=CE==3.
∵OA=AB=8,
∴OF=OA-AF=5.
∴点C(5,4).
∵点C在y=的图象上,
∴k=5×4=20.
(2)∵BC=BD=5,AB=8,
∴AD=AB-BD=3.
设点A的坐标为(m,0),则C,D两点的坐标分别为(m-3,4),(m,3).
∵点C,D在y=的图象上,
∴4(m-3)=3m,
∴m=12.
∴点A(12,0),C(9,4),D(12,3).
∴S△OAC=×12×4=24.
6.解:(1)将点A(1,2)代入反比例函数解析式,得k=1×2=2.
∴反比例函数的解析式为y1=.
由题图知当y1>y2时,x的取值范围是02.
(2)存在.
将x=2代入y1=,得y=1.
∴点C的坐标为(2,1).
∴OC=.
当OC=OM时,OM=,
∴点M的坐标为(0,)或(0,-).
当CM=CO时,
点C在OM的垂直平分线上,
又∵点C的坐标为(2,1),
∴点M的坐标为(0,2).
当MO=MC时,
点M在OC的垂直平分线上,
如图,过点C作CN⊥y轴于点N.
令MO=m,
则MC=m,MN=m-1.
在Rt△CMN中,
CN2+MN2=MC2.
即22+(m-1)2=m2,
解得m=.
∴点M的坐标为.
综上所述,点M的坐标为(0,)或(0,-)或(0,2)或.
反比例函数的图象
1.反比例函数y=-的图象大致是 ( )
A. B. C. D.
2.如果反比例函数的图象经过点(-3,-4),那么函数的图象在第 象限.
反比例函数的性质
3.(2024唐山滦南县期末)已知反比例函数y=.下列说法正确的是 ( )
A.图象经过点(-3,1)
B.y随x的增大而减小
C.图象不可能和x轴相交
D.图象是轴对称图形但不是中心对称图形
用待定系数法求反比例函数解析式
4.如图,反比例函数y=的图象经过点A(2,1),该反比例函数的解析式为 ( )
A.y= B.y=- C.y= D.y=-
反比例函数y=的几何意义
5.反比例函数y=(x<0)的图象如图所示,AB∥y轴,若△ABC的面积为3,则k的值为 ( )
A. B.- C.3 D.-6
6.如图,矩形OABC的面积是4,点B在反比例函数y=的图象上.此反比例函数的解析式为 .
7.(2024龙岩期末)如图,反比例函数y=的图象的一支位于第一象限.
(1)该函数图象的另一支在第 象限,k的取值范围是 .
(2)点A在反比例函数的图象上,点A关于x轴的对称点为点B,点A关于原点的对称点为点C.若△ABC的面积为4,求k的值.
1.如图,满足函数y=k(x-1)和y=(k≠0)的大致图象是 ( )
① ② ③ ④
A.①② B.②③ C.②④ D.①④
2.对于反比例函数y=-,下列说法正确的是 ( )
A.图象经过点(2,-3)
B.图象位于第一、第三象限
C.y随x的增大而增大
D.当0
4.如图,在平面直角坐标系中,△AOB的边OB在y轴上,边AB与x轴交于点D,且BD=AD,反比例函数y=(x>0)的图象经过点A.若S△OAB=1,则反比例函数的解析式为 .
5.如图,在△ABC中,AC=BC=5,AB=8,AB⊥x轴,垂足为A,反比例函数y=(x>0)的图象经过点C,交AB于点D.
(1)若OA=AB,求k的值.
(2)若BC=BD,连接OC,求△OAC的面积.
6.(几何直观)如图,过原点O的直线与反比例函数y1=(k≠0)的图象交于A(1,2),B两点,一次函数y2=mx+b(m≠0)的图象过点A与反比例函数交于另一点C(2,n).
(1)求反比例函数的解析式;当y1>y2时,根据图象直接写出x的取值范围.
(2)在y轴上是否存在点M,使得△COM为等腰三角形 若存在,求出点M的坐标;若不存在,请说明理由.
【详解答案】
课堂达标
1.B 解析:在反比例函数y=-中,k=-6<0,图象在第二、第四象限.故选B.
2.一、第三 解析:设反比例函数的解析式为y=(k≠0).∵反比例函数的图象经过点(-3,-4),∴k=(-3)×(-4)=12.
∴函数的图象在第一、第三象限.
3.C 解析:A.∵(-3)×1=-3≠3,∴图象不经过点(-3,1).原说法错误,不符合题意;B.∵k=3>0,∴函数图象的两个分支分别位于第一、第三象限.在每一象限内,y随x的增大而减小.原说法错误,不符合题意;C.∵函数y=是反比例函数,∴图象不可能和x轴相交.原说法正确,符合题意;D.∵函数y=是反比例函数,∴图象是中心对称图形.原说法错误,不符合题意.故选C.
4.C 解析:∵反比例函数y=的图象经过点A(2,1),∴1=.∴k=2.∴该反比例函数的解析式为y=.故选C.
5.D 解析:如图,连接OA.∵AB∥y轴,∴△ABC的面积=△OAB的面积.∵2S△OAB=2×3=6,∴|k|=6.∵反比例函数图象在第二象限,∴k=-6.故选D.
6.y= 解析:设BC=a,AB=b,则点B的坐标为(-a,-b),AB·BC=ab=4.将点B(-a,-b)代入y=中,得k=xy=(-a)×(-b)=ab=4.∴反比例函数的解析式为y=.
7.解:(1)三 k>3
(2)由题意,设点A的坐标为(a,b).
∵点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,点C与点A关于原点O对称,
∴a>0,b>0,点B的坐标是(a,-b),点C的坐标是(-a,-b).
∴BC=a-(-a)=2a,AB=b-(-b)=2b.
∵△ABC的面积为4,∴×AB×BC=4.
∴×2a×2b=4.∴ab=2.
∵点A在反比例函数y=位于第一象限的图象上,
∴k-3=ab=2.解得k=5.
课后提升
1.B 解析:∵y=k(x-1),∴函数y=k(x-1)图象过点(1,0).故①④不符合题意;当k>0时,函数y=k(x-1)过第一、第三、第四象限,函数y=(k≠0)在第一、第三象限;当k<0时,函数y=k(x-1)过第一、第二、第四象限,函数y=(k≠0)在第二、第四象限.故②③符合题意.故选B.
2.D 解析:反比例函数y=-.A.当x=2时,y=-,图象经过点2,-,故选项A不符合题意;B.∵k=-5<0,故该函数图象位于第二、第四象限,故选项B不符合题意;C.在每个象限内,y随x的增大而增大,故选项C不符合题意;D.∵当x=1时,y=-5,x>0时,y<0,∴当0
4.y= 解析:如图,过点A作x轴的垂线与x轴交于点C.
设点A(a,b),则AC=b,OC=a,AC∥OB.∴∠ACD=∠BOD=90°,∠ADC=∠BDO.∵AD=BD,∴△ADC≌△BDO(AAS).∴S△ADC=S△BDO.∴S△OAC=S△AOD+S△ADC=S△AOD+S△BDO=S△OAB=1.∴×OC×AC=ab=1.∴ab=2,∵点A(a,b)在y=上,∴k=ab=2.∴反比例函数的解析式为y=.
5.解:(1)如图,过点C作CE⊥AB于点E,CF⊥OA于点F,∴四边形AECF为矩形.
∴CF=AE,CE=AF.
∵AB=8,AC=BC=5,CE⊥AB,
∴BE=AE=CF=4.
∴AF=CE==3.
∵OA=AB=8,
∴OF=OA-AF=5.
∴点C(5,4).
∵点C在y=的图象上,
∴k=5×4=20.
(2)∵BC=BD=5,AB=8,
∴AD=AB-BD=3.
设点A的坐标为(m,0),则C,D两点的坐标分别为(m-3,4),(m,3).
∵点C,D在y=的图象上,
∴4(m-3)=3m,
∴m=12.
∴点A(12,0),C(9,4),D(12,3).
∴S△OAC=×12×4=24.
6.解:(1)将点A(1,2)代入反比例函数解析式,得k=1×2=2.
∴反比例函数的解析式为y1=.
由题图知当y1>y2时,x的取值范围是0
(2)存在.
将x=2代入y1=,得y=1.
∴点C的坐标为(2,1).
∴OC=.
当OC=OM时,OM=,
∴点M的坐标为(0,)或(0,-).
当CM=CO时,
点C在OM的垂直平分线上,
又∵点C的坐标为(2,1),
∴点M的坐标为(0,2).
当MO=MC时,
点M在OC的垂直平分线上,
如图,过点C作CN⊥y轴于点N.
令MO=m,
则MC=m,MN=m-1.
在Rt△CMN中,
CN2+MN2=MC2.
即22+(m-1)2=m2,
解得m=.
∴点M的坐标为.
综上所述,点M的坐标为(0,)或(0,-)或(0,2)或.
