27.1 图形的相似 课时作业(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 27.1 图形的相似 课时作业(含答案) 2024-2025学年数学人教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 20:30:15 | ||
图片预览

文档简介
27.1 图形的相似
相似图形
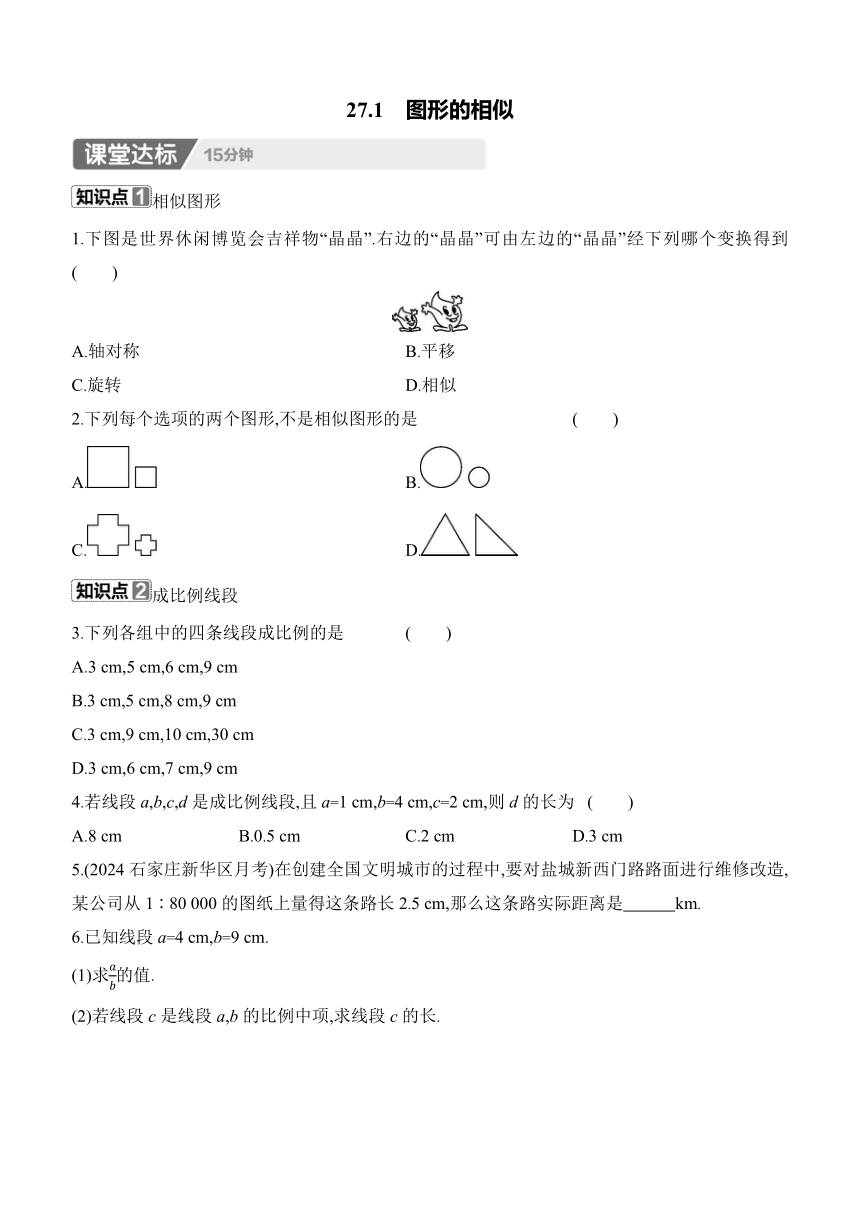
1.下图是世界休闲博览会吉祥物“晶晶”.右边的“晶晶”可由左边的“晶晶”经下列哪个变换得到 ( )
A.轴对称 B.平移
C.旋转 D.相似
2.下列每个选项的两个图形,不是相似图形的是 ( )
A. B.
C. D.
成比例线段
3.下列各组中的四条线段成比例的是 ( )
A.3 cm,5 cm,6 cm,9 cm
B.3 cm,5 cm,8 cm,9 cm
C.3 cm,9 cm,10 cm,30 cm
D.3 cm,6 cm,7 cm,9 cm
4.若线段a,b,c,d是成比例线段,且a=1 cm,b=4 cm,c=2 cm,则d的长为 ( )
A.8 cm B.0.5 cm C.2 cm D.3 cm
5.(2024石家庄新华区月考)在创建全国文明城市的过程中,要对盐城新西门路路面进行维修改造,某公司从1∶80 000的图纸上量得这条路长2.5 cm,那么这条路实际距离是 km.
6.已知线段a=4 cm,b=9 cm.
(1)求的值.
(2)若线段c是线段a,b的比例中项,求线段c的长.
相似多边形
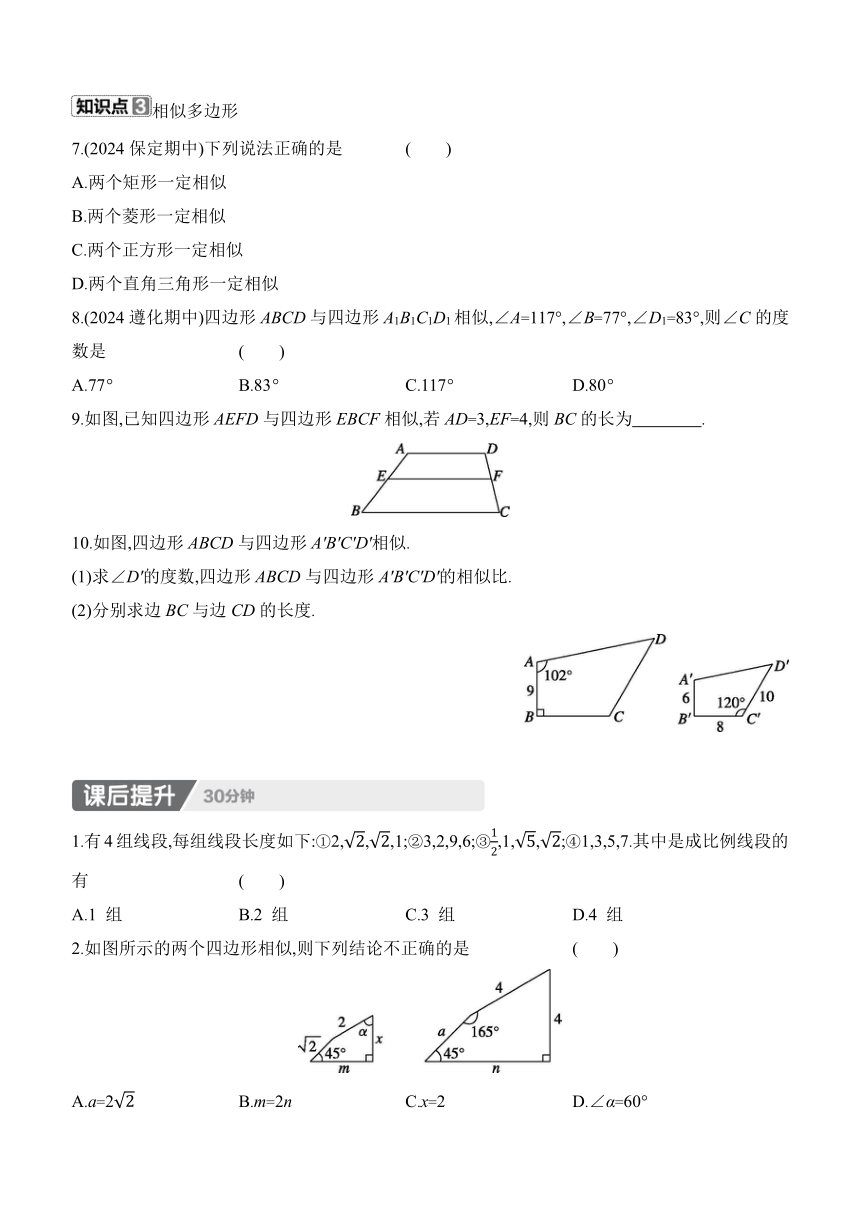
7.(2024保定期中)下列说法正确的是 ( )
A.两个矩形一定相似
B.两个菱形一定相似
C.两个正方形一定相似
D.两个直角三角形一定相似
8.(2024遵化期中)四边形ABCD与四边形A1B1C1D1相似,∠A=117°,∠B=77°,∠D1=83°,则∠C的度数是 ( )
A.77° B.83° C.117° D.80°
9.如图,已知四边形AEFD与四边形EBCF相似,若AD=3,EF=4,则BC的长为 .
10.如图,四边形ABCD与四边形A'B'C'D'相似.
(1)求∠D'的度数,四边形ABCD与四边形A'B'C'D'的相似比.
(2)分别求边BC与边CD的长度.
1.有4组线段,每组线段长度如下:①2,,,1;②3,2,9,6;③,1,,;④1,3,5,7.其中是成比例线段的有 ( )
A.1 组 B.2 组 C.3 组 D.4 组
2.如图所示的两个四边形相似,则下列结论不正确的是 ( )
A.a=2 B.m=2n C.x=2 D.∠α=60°
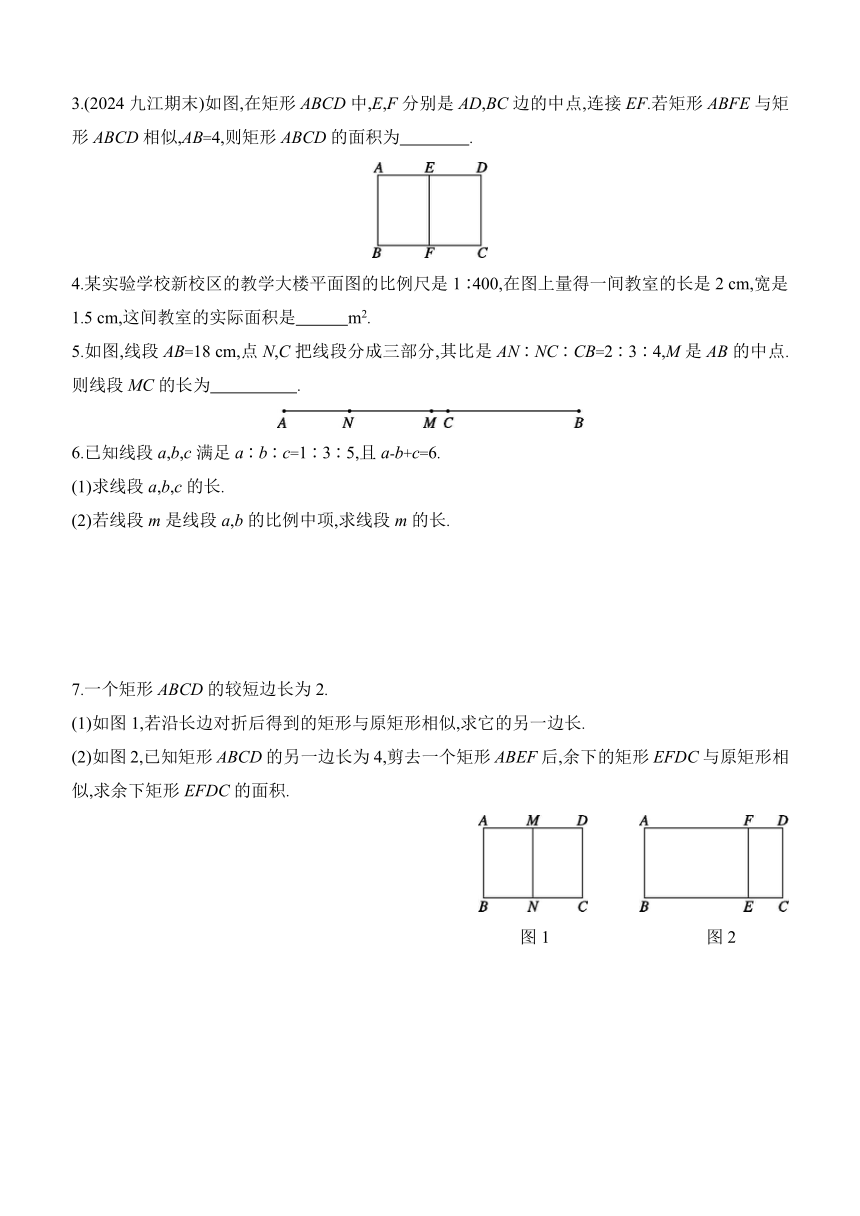
3.(2024九江期末)如图,在矩形ABCD中,E,F分别是AD,BC边的中点,连接EF.若矩形ABFE与矩形ABCD相似,AB=4,则矩形ABCD的面积为 .
4.某实验学校新校区的教学大楼平面图的比例尺是1∶400,在图上量得一间教室的长是2 cm,宽是1.5 cm,这间教室的实际面积是 m2.
5.如图,线段AB=18 cm,点N,C把线段分成三部分,其比是AN∶NC∶CB=2∶3∶4,M是AB的中点.则线段MC的长为 .
6.已知线段a,b,c满足a∶b∶c=1∶3∶5,且a-b+c=6.
(1)求线段a,b,c的长.
(2)若线段m是线段a,b的比例中项,求线段m的长.
7.一个矩形ABCD的较短边长为2.
(1)如图1,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长.
(2)如图2,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
图1 图2
8.(几何直观)宽与长的比是的矩形叫黄金矩形,如图1,已知矩形ABCD的宽AB=1.将图1中的矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF如图2,已知矩形DCEF为黄金矩形,计算点D到线段AE的距离.
图1 图2
【详解答案】
课堂达标
1.D 解析:A.轴对称变换是反射产生一个图形的映像的过程,不符合题意,故错误;B.平移变换是原图形中的点都沿着平行的途径运动一个恒等的距离,不符合题意,故错误;C.旋转变换是原图形中的点都绕着一个固定的中心点转动一个恒等的角度,不符合题意,故错误;D.相似变换,图形的形状相同,但大小不一定相同的变换,符合题意,故正确.故选D.
2.D 解析:A.形状相同,符合相似图形的定义,此选项不符合题意;B.形状相同,符合相似图形的定义,此选项不符合题意;C.形状相同,符合相似图形的定义,此选项不符合题意;D.形状不相同,不符合相似图形的定义,此选项符合题意.故选D.
3.C 解析:A.∵3×9≠5×6,∴四条线段不成比例.故A选项不符合题意;B.∵3×9≠5×8,∴四条线段不成比例.故B选项不符合题意;C.∵3×30=9×10,∴四条线段成比例.故C选项符合题意;D.∵3×9≠6×7,∴四条线段不成比例.故D选项不符合题意.故选C.
4.A 解析:∵a,b,c,d是成比例线段,∴ad=cb.∵a=1 cm,b=4 cm,c=2 cm,∴d=8 cm.故选A.
5.2 解析:由题意,得2.5÷=200 000(cm).200 000 cm=2 km.
6.解:(1).
(2)∵线段c是线段a,b的比例中项,a=4 cm,b=9 cm,∴c2=ab=36.解得c=±6.又∵线段的长是正数,∴c=6 cm.
7.C 解析:A.两个矩形满足对应角相等但不一定满足对应边的比相等,故不一定相似,不符合题意;B.两个菱形满足对应边的比相等但不一定满足对应角相等,故不一定相似,不符合题意;C.两个正方形一定相似,正确,符合题意;D.两个直角三角形不一定相似,不符合题意.故选C.
8.B 解析:∵四边形ABCD与四边形A1B1C1D1相似,∴∠D=∠D1=83°.又∵∠A=117°,∠B=77°,∴∠C=360°-117°-77°-83°=83°.故选B.
9. 解析:∵四边形AEFD与四边形EBCF相似,
∴AD∶EF=EF∶BC.∵AD=3,EF=4,∴3∶4=4∶BC.∴BC=.
10.解:(1)∵四边形ABCD与四边形A'B'C'D'相似,
∴∠A=∠A'=102°,∠B=∠B'=90°,∠C=∠C'=120°.
∴∠D'=360°-102°-90°-120°=48°,
相似比为.
(2)∵四边形ABCD与四边形A'B'C'D'相似,
∴.
∴BC=×8=12,CD=×10=15.
课后提升
1.B 解析:∵2×1=,∴①是成比例线段;∵3×6=2×9,②是成比例线段;∵≠1×,1×7≠3×5,∴③④不是成比例线段.由上可知可组成比例线段的有2组.故选B.
2.B 解析:∵两个四边形相似,∴相似比为2∶4=1∶2.∴∶a=x∶4=m∶n=1∶2.解得a=2,x=2,2m=n.∴∠α=360°-45°-90°-165°=60°.综上所述,只有选项B符合题意.故选B.
3.16 解析:设AE=x,则AD=2AE=2x.∵矩形ABFE与矩形ABCD相似,∴,即.解得x=2.∴AD=2x=4.∴矩形ABCD的面积为AB·AD=4×4=16.
4.48 解析:由题意知,这间教室的实际长为2×400=800(cm)=8 m,实际宽为1.5×400=600(cm)=6 m.∴这间教室的实际面积为8×6=48(m2).
5.1 cm 解析:∵点N,C把线段AB分成三部分,其比是AN∶NC∶CB=2∶3∶4,∴设AN=2x,NC=3x,CB=4x.∵线段AB=18 cm,∴2x+3x+4x=18.解得x=2.∴AC=5x=10 cm.∵M是AB的中点.∴AM=AB=9 cm.∴CM=AC-AM=10-9=1(cm).
6.解:(1)设a=k,b=3k,c=5k.
∵a-b+c=6,∴k-3k+5k=6.
解得k=2.
∴a=2,b=6,c=10.
(2)由(1)知a=2,b=6,又∵线段m是线段a,b的比例中项,
∴m2=ab,即m2=2×6=12.∴m=±2.
∵m>0,∴m=2.
7.解:(1)由题意,得MN=AB=2,MD=AD=BC,
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似.
∴.
∴DM·BC=AB·MN,即BC2=4,
∴BC=2,即它的另一边长为2.
(2)∵矩形EFDC与原矩形ABCD相似,
∴.
∵AB=CD=2,BC=4,
∴DF==1.
∴矩形EFDC的面积为CD·DF=2×1=2.
8.解:∵四边形ABEF是正方形,
∴EF=AF=AB=1.
∵矩形DCEF是黄金矩形,
∴.∴DF=.
∴AD=DF+AF=+1=.
如图,过点D作DG⊥AE于点G.
在Rt△ABE中,AB=BE=1,∠B=90°,
根据勾股定理,得
AE=.
∵AD=BC=,EF=1,
∴S△AED=AD·EF=AE·DG,
∴DG=.
∴点D到线段AE的距离为.
相似图形
1.下图是世界休闲博览会吉祥物“晶晶”.右边的“晶晶”可由左边的“晶晶”经下列哪个变换得到 ( )
A.轴对称 B.平移
C.旋转 D.相似
2.下列每个选项的两个图形,不是相似图形的是 ( )
A. B.
C. D.
成比例线段
3.下列各组中的四条线段成比例的是 ( )
A.3 cm,5 cm,6 cm,9 cm
B.3 cm,5 cm,8 cm,9 cm
C.3 cm,9 cm,10 cm,30 cm
D.3 cm,6 cm,7 cm,9 cm
4.若线段a,b,c,d是成比例线段,且a=1 cm,b=4 cm,c=2 cm,则d的长为 ( )
A.8 cm B.0.5 cm C.2 cm D.3 cm
5.(2024石家庄新华区月考)在创建全国文明城市的过程中,要对盐城新西门路路面进行维修改造,某公司从1∶80 000的图纸上量得这条路长2.5 cm,那么这条路实际距离是 km.
6.已知线段a=4 cm,b=9 cm.
(1)求的值.
(2)若线段c是线段a,b的比例中项,求线段c的长.
相似多边形
7.(2024保定期中)下列说法正确的是 ( )
A.两个矩形一定相似
B.两个菱形一定相似
C.两个正方形一定相似
D.两个直角三角形一定相似
8.(2024遵化期中)四边形ABCD与四边形A1B1C1D1相似,∠A=117°,∠B=77°,∠D1=83°,则∠C的度数是 ( )
A.77° B.83° C.117° D.80°
9.如图,已知四边形AEFD与四边形EBCF相似,若AD=3,EF=4,则BC的长为 .
10.如图,四边形ABCD与四边形A'B'C'D'相似.
(1)求∠D'的度数,四边形ABCD与四边形A'B'C'D'的相似比.
(2)分别求边BC与边CD的长度.
1.有4组线段,每组线段长度如下:①2,,,1;②3,2,9,6;③,1,,;④1,3,5,7.其中是成比例线段的有 ( )
A.1 组 B.2 组 C.3 组 D.4 组
2.如图所示的两个四边形相似,则下列结论不正确的是 ( )
A.a=2 B.m=2n C.x=2 D.∠α=60°
3.(2024九江期末)如图,在矩形ABCD中,E,F分别是AD,BC边的中点,连接EF.若矩形ABFE与矩形ABCD相似,AB=4,则矩形ABCD的面积为 .
4.某实验学校新校区的教学大楼平面图的比例尺是1∶400,在图上量得一间教室的长是2 cm,宽是1.5 cm,这间教室的实际面积是 m2.
5.如图,线段AB=18 cm,点N,C把线段分成三部分,其比是AN∶NC∶CB=2∶3∶4,M是AB的中点.则线段MC的长为 .
6.已知线段a,b,c满足a∶b∶c=1∶3∶5,且a-b+c=6.
(1)求线段a,b,c的长.
(2)若线段m是线段a,b的比例中项,求线段m的长.
7.一个矩形ABCD的较短边长为2.
(1)如图1,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长.
(2)如图2,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.
图1 图2
8.(几何直观)宽与长的比是的矩形叫黄金矩形,如图1,已知矩形ABCD的宽AB=1.将图1中的矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF如图2,已知矩形DCEF为黄金矩形,计算点D到线段AE的距离.
图1 图2
【详解答案】
课堂达标
1.D 解析:A.轴对称变换是反射产生一个图形的映像的过程,不符合题意,故错误;B.平移变换是原图形中的点都沿着平行的途径运动一个恒等的距离,不符合题意,故错误;C.旋转变换是原图形中的点都绕着一个固定的中心点转动一个恒等的角度,不符合题意,故错误;D.相似变换,图形的形状相同,但大小不一定相同的变换,符合题意,故正确.故选D.
2.D 解析:A.形状相同,符合相似图形的定义,此选项不符合题意;B.形状相同,符合相似图形的定义,此选项不符合题意;C.形状相同,符合相似图形的定义,此选项不符合题意;D.形状不相同,不符合相似图形的定义,此选项符合题意.故选D.
3.C 解析:A.∵3×9≠5×6,∴四条线段不成比例.故A选项不符合题意;B.∵3×9≠5×8,∴四条线段不成比例.故B选项不符合题意;C.∵3×30=9×10,∴四条线段成比例.故C选项符合题意;D.∵3×9≠6×7,∴四条线段不成比例.故D选项不符合题意.故选C.
4.A 解析:∵a,b,c,d是成比例线段,∴ad=cb.∵a=1 cm,b=4 cm,c=2 cm,∴d=8 cm.故选A.
5.2 解析:由题意,得2.5÷=200 000(cm).200 000 cm=2 km.
6.解:(1).
(2)∵线段c是线段a,b的比例中项,a=4 cm,b=9 cm,∴c2=ab=36.解得c=±6.又∵线段的长是正数,∴c=6 cm.
7.C 解析:A.两个矩形满足对应角相等但不一定满足对应边的比相等,故不一定相似,不符合题意;B.两个菱形满足对应边的比相等但不一定满足对应角相等,故不一定相似,不符合题意;C.两个正方形一定相似,正确,符合题意;D.两个直角三角形不一定相似,不符合题意.故选C.
8.B 解析:∵四边形ABCD与四边形A1B1C1D1相似,∴∠D=∠D1=83°.又∵∠A=117°,∠B=77°,∴∠C=360°-117°-77°-83°=83°.故选B.
9. 解析:∵四边形AEFD与四边形EBCF相似,
∴AD∶EF=EF∶BC.∵AD=3,EF=4,∴3∶4=4∶BC.∴BC=.
10.解:(1)∵四边形ABCD与四边形A'B'C'D'相似,
∴∠A=∠A'=102°,∠B=∠B'=90°,∠C=∠C'=120°.
∴∠D'=360°-102°-90°-120°=48°,
相似比为.
(2)∵四边形ABCD与四边形A'B'C'D'相似,
∴.
∴BC=×8=12,CD=×10=15.
课后提升
1.B 解析:∵2×1=,∴①是成比例线段;∵3×6=2×9,②是成比例线段;∵≠1×,1×7≠3×5,∴③④不是成比例线段.由上可知可组成比例线段的有2组.故选B.
2.B 解析:∵两个四边形相似,∴相似比为2∶4=1∶2.∴∶a=x∶4=m∶n=1∶2.解得a=2,x=2,2m=n.∴∠α=360°-45°-90°-165°=60°.综上所述,只有选项B符合题意.故选B.
3.16 解析:设AE=x,则AD=2AE=2x.∵矩形ABFE与矩形ABCD相似,∴,即.解得x=2.∴AD=2x=4.∴矩形ABCD的面积为AB·AD=4×4=16.
4.48 解析:由题意知,这间教室的实际长为2×400=800(cm)=8 m,实际宽为1.5×400=600(cm)=6 m.∴这间教室的实际面积为8×6=48(m2).
5.1 cm 解析:∵点N,C把线段AB分成三部分,其比是AN∶NC∶CB=2∶3∶4,∴设AN=2x,NC=3x,CB=4x.∵线段AB=18 cm,∴2x+3x+4x=18.解得x=2.∴AC=5x=10 cm.∵M是AB的中点.∴AM=AB=9 cm.∴CM=AC-AM=10-9=1(cm).
6.解:(1)设a=k,b=3k,c=5k.
∵a-b+c=6,∴k-3k+5k=6.
解得k=2.
∴a=2,b=6,c=10.
(2)由(1)知a=2,b=6,又∵线段m是线段a,b的比例中项,
∴m2=ab,即m2=2×6=12.∴m=±2.
∵m>0,∴m=2.
7.解:(1)由题意,得MN=AB=2,MD=AD=BC,
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似.
∴.
∴DM·BC=AB·MN,即BC2=4,
∴BC=2,即它的另一边长为2.
(2)∵矩形EFDC与原矩形ABCD相似,
∴.
∵AB=CD=2,BC=4,
∴DF==1.
∴矩形EFDC的面积为CD·DF=2×1=2.
8.解:∵四边形ABEF是正方形,
∴EF=AF=AB=1.
∵矩形DCEF是黄金矩形,
∴.∴DF=.
∴AD=DF+AF=+1=.
如图,过点D作DG⊥AE于点G.
在Rt△ABE中,AB=BE=1,∠B=90°,
根据勾股定理,得
AE=.
∵AD=BC=,EF=1,
∴S△AED=AD·EF=AE·DG,
∴DG=.
∴点D到线段AE的距离为.
