27.2.3 相似三角形应用举例 课时作业(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 27.2.3 相似三角形应用举例 课时作业(含答案) 2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 209.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 00:00:00 | ||
图片预览



文档简介
27.2.3 相似三角形应用举例
测量物高
1.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=60 cm,EF=30 cm,测得边DF离地面的高度AC=1.5 m,CD=10 m,则树高AB为 ( )
A.5 m B.6.5 m C.7 m D.7.5 m
2.(2024昆明嵩明县期末)据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图1所示.在如图2所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是 cm.
图1 图2
3.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器CD,测得∠ACD=135°;再在BD的延长线上确定一点G,使DG=5 m,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2 m,小明眼睛与地面的距离EF=1.6 m,测量器的高度CD=0.5 m.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,则这棵古树的高AB为多少米 (小平面镜的大小忽略不计)
测量距离或宽度
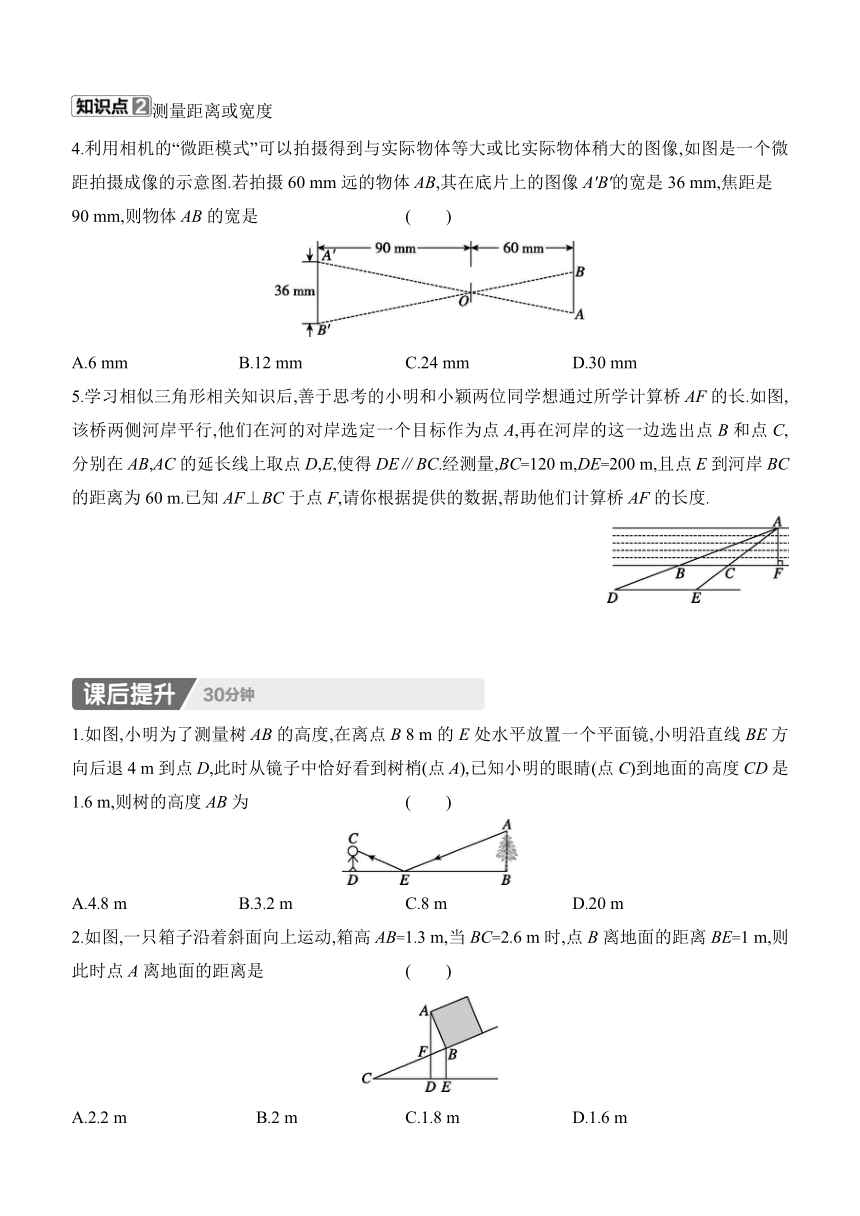
4.利用相机的“微距模式”可以拍摄得到与实际物体等大或比实际物体稍大的图像,如图是一个微距拍摄成像的示意图.若拍摄60 mm远的物体AB,其在底片上的图像A'B'的宽是36 mm,焦距是
90 mm,则物体AB的宽是 ( )
A.6 mm B.12 mm C.24 mm D.30 mm
5.学习相似三角形相关知识后,善于思考的小明和小颖两位同学想通过所学计算桥AF的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB,AC的延长线上取点D,E,使得DE∥BC.经测量,BC=120 m,DE=200 m,且点E到河岸BC的距离为60 m.已知AF⊥BC于点F,请你根据提供的数据,帮助他们计算桥AF的长度.
1.如图,小明为了测量树AB的高度,在离点B 8 m的E处水平放置一个平面镜,小明沿直线BE方向后退4 m到点D,此时从镜子中恰好看到树梢(点A),已知小明的眼睛(点C)到地面的高度CD是1.6 m,则树的高度AB为 ( )
A.4.8 m B.3.2 m C.8 m D.20 m
2.如图,一只箱子沿着斜面向上运动,箱高AB=1.3 m,当BC=2.6 m时,点B离地面的距离BE=1 m,则此时点A离地面的距离是 ( )
A.2.2 m B.2 m C.1.8 m D.1.6 m
3.如图,某校宣传栏BC后面12 m处种有一排与宣传栏平行的若干棵树,即BC∥DE,且相邻两棵树的间隔为2 m,一人站在距宣传栏前面的A处正好看到两端的树干,其余的树均被宣传栏挡住.已知AF⊥BC,AF=3 m,BC=10 m,该宣传栏后DE处共有多少棵树 (不计宣传栏的厚度)
4.(2024保定期末)问题:如图,小明和爸爸的身高分别是1.5 m,1.8 m,即EB=1.5 m,FC=1.8 m,二人配合测量树的高度AD.
操作:小明在距离树0.3 m的B处(AB=0.3 m)看树的顶端D的视线为ED,原地再看爸爸的头部,视线为EF,爸爸可以前后移动,当EF⊥ED时爸爸站着不动,这时小明测得AC=9.5 m.
问题解决:已知点A,B,C在地平面的一条直线上,树和二人都垂直于这条直线,求树的高度AD.
5.(应用意识)【学科融合】如图1,在反射现象中,反射光线、入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;反射角r等于入射角i.这就是光的反射定律.
【问题解决】如图2,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度DE=3.5 m,点F到地面的高度CF=1.5 m,灯泡到木板的水平距离AC=5.4 m,木板到墙的水平距离为CD=4 m.图中点A,B,C,D在同一条直线上.
(1)求BC的长.
(2)求灯泡到地面的高度AG.
图1 图2
【详解答案】
课堂达标
1.B 解析:DE=60 cm=0.6 m,EF=30 cm=0.3 m,
在△DEF和△DCB中,
∴△DEF∽△DCB.
∴,即.
解得BC=5.
∵AC=1.5 m,
∴AB=AC+BC=1.5+5=6.5(m),
即树高6.5 m.故选B.
2.4 解析:设蜡烛火焰的高度是x cm.
由相似三角形的性质,得.
解得x=4.
∴蜡烛火焰的高度是4 cm.
3.解:如图,过点C作CH⊥AB于点H.
∴四边形CHBD为矩形.∠DCH=90°.
∴CH=BD,BH=CD=0.5 m.
∵∠ACD=135°,
∴∠ACH=∠ACD-∠DCH=45°.
在Rt△ACH中,∠ACH=45°,
∴AH=CH=BD.
∴AB=AH+BH=BD+0.5.
∵EF⊥FB,AB⊥FB,
∴∠EFG=∠ABG=90°.
由反射角等于入射角,得∠EGF=∠AGB.
∴△EFG∽△ABG.
∴.
∴.
解得BD=17.5.
∴AB=17.5+0.5=18(m).
∴这棵古树的高AB为18 m.
4.C 解析:∵AB∥A'B',
∴△ABO∽△A'B'O.
∴.
∴.
∴AB=24 mm.
∴物体AB的宽是24 mm.故选C.
5.解:如图,过点E作EG⊥BC于点G,
∵DE∥BC,∴△ABC∽△ADE.
∴.
∴.
∵AF⊥BC,EG⊥BC.
∴AF∥EG.
∴△ACF∽△ECG.
∴,即.
解得AF=90.
∴桥AF的长度为90 m.
课后提升
1.B 解析:由题意,得AB⊥BD,CD⊥BD.
∴∠ABE=∠CDE=90°.
由光的反射原理,得∠AEB=∠CED.
∴△AEB∽△CED.
∴.
∵BE=8 m,DE=4 m,CD=1.6 m,
∴.
∴AB=3.2 m.故选B.
2.A 解析:由题意,得AD∥BE,则∠CFD=∠AFB=∠CBE,△CDF∽△CEB.
∵∠CEB=∠ABF=90°,∠CBE=∠AFB,
∴△CBE∽△AFB.
∴.
∵BC=2.6 m,BE=1 m,
∴CE==2.4 m.
∴.
解得FB=,AF=.
∵△CDF∽△CEB,
∴,
即.
解得DF=.
∴AD=AF+DF==2.2(m).
∴此时点A离地面的距离为2.2 m.
故选A.
3.解:如图,延长AF,交DE于点G.
∵BC∥DE,
∴△ABC∽△ADE,AG⊥ED.
∴.
又∵BC=10 m,AF=3 m,FG=12 m,
∴AG=AF+FG=15 m.
∴.
∴DE=50 m.
∴50÷2+1=26(棵).
∴宣传栏后DE处共有26棵树.
4.解:如图,过点E作EG⊥CF于点G,延长GE交AD于点H,则GH⊥AD.
∵CF⊥AC,AD⊥AC,BE⊥AC,
∴四边形CBEG,四边形AHEB是矩形.
∴AH=BE=CG=1.5 m,BC=EG=9.5-0.3=9.2(m),AB=HE=0.3 m.
∵∠FGE=∠EHD=∠FED=90°,
∴∠EFG+∠FEG=∠FEG+∠DEH=90°.
∴∠EFG=∠DEH.
∴△EFG∽△DEH.
∴.
∴.
∴DH=9.2 m.
∴AD=DH+AH=9.2+1.5=10.7(m).
∴树的高度AD为10.7 m.
5.解:(1)由题意,得FC∥DE.
∴△BFC∽△BED.
∴.
∴.
∴BC=3 m.
∴BC的长为3 m.
(2)∵AC=5.4 m.
∴AB=5.4-3=2.4(m).
∵光在镜面反射中的反射角等于入射角,
∴∠GBA=∠FBC.
又∵∠GAB=∠FCB,
∴△BGA∽△BFC.
∴.
∴.
∴AG=1.2 m.
∴灯泡到地面的高度AG为1.2 m.
测量物高
1.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=60 cm,EF=30 cm,测得边DF离地面的高度AC=1.5 m,CD=10 m,则树高AB为 ( )
A.5 m B.6.5 m C.7 m D.7.5 m
2.(2024昆明嵩明县期末)据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图1所示.在如图2所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是 cm.
图1 图2
3.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器CD,测得∠ACD=135°;再在BD的延长线上确定一点G,使DG=5 m,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2 m,小明眼睛与地面的距离EF=1.6 m,测量器的高度CD=0.5 m.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,则这棵古树的高AB为多少米 (小平面镜的大小忽略不计)
测量距离或宽度
4.利用相机的“微距模式”可以拍摄得到与实际物体等大或比实际物体稍大的图像,如图是一个微距拍摄成像的示意图.若拍摄60 mm远的物体AB,其在底片上的图像A'B'的宽是36 mm,焦距是
90 mm,则物体AB的宽是 ( )
A.6 mm B.12 mm C.24 mm D.30 mm
5.学习相似三角形相关知识后,善于思考的小明和小颖两位同学想通过所学计算桥AF的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB,AC的延长线上取点D,E,使得DE∥BC.经测量,BC=120 m,DE=200 m,且点E到河岸BC的距离为60 m.已知AF⊥BC于点F,请你根据提供的数据,帮助他们计算桥AF的长度.
1.如图,小明为了测量树AB的高度,在离点B 8 m的E处水平放置一个平面镜,小明沿直线BE方向后退4 m到点D,此时从镜子中恰好看到树梢(点A),已知小明的眼睛(点C)到地面的高度CD是1.6 m,则树的高度AB为 ( )
A.4.8 m B.3.2 m C.8 m D.20 m
2.如图,一只箱子沿着斜面向上运动,箱高AB=1.3 m,当BC=2.6 m时,点B离地面的距离BE=1 m,则此时点A离地面的距离是 ( )
A.2.2 m B.2 m C.1.8 m D.1.6 m
3.如图,某校宣传栏BC后面12 m处种有一排与宣传栏平行的若干棵树,即BC∥DE,且相邻两棵树的间隔为2 m,一人站在距宣传栏前面的A处正好看到两端的树干,其余的树均被宣传栏挡住.已知AF⊥BC,AF=3 m,BC=10 m,该宣传栏后DE处共有多少棵树 (不计宣传栏的厚度)
4.(2024保定期末)问题:如图,小明和爸爸的身高分别是1.5 m,1.8 m,即EB=1.5 m,FC=1.8 m,二人配合测量树的高度AD.
操作:小明在距离树0.3 m的B处(AB=0.3 m)看树的顶端D的视线为ED,原地再看爸爸的头部,视线为EF,爸爸可以前后移动,当EF⊥ED时爸爸站着不动,这时小明测得AC=9.5 m.
问题解决:已知点A,B,C在地平面的一条直线上,树和二人都垂直于这条直线,求树的高度AD.
5.(应用意识)【学科融合】如图1,在反射现象中,反射光线、入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;反射角r等于入射角i.这就是光的反射定律.
【问题解决】如图2,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度DE=3.5 m,点F到地面的高度CF=1.5 m,灯泡到木板的水平距离AC=5.4 m,木板到墙的水平距离为CD=4 m.图中点A,B,C,D在同一条直线上.
(1)求BC的长.
(2)求灯泡到地面的高度AG.
图1 图2
【详解答案】
课堂达标
1.B 解析:DE=60 cm=0.6 m,EF=30 cm=0.3 m,
在△DEF和△DCB中,
∴△DEF∽△DCB.
∴,即.
解得BC=5.
∵AC=1.5 m,
∴AB=AC+BC=1.5+5=6.5(m),
即树高6.5 m.故选B.
2.4 解析:设蜡烛火焰的高度是x cm.
由相似三角形的性质,得.
解得x=4.
∴蜡烛火焰的高度是4 cm.
3.解:如图,过点C作CH⊥AB于点H.
∴四边形CHBD为矩形.∠DCH=90°.
∴CH=BD,BH=CD=0.5 m.
∵∠ACD=135°,
∴∠ACH=∠ACD-∠DCH=45°.
在Rt△ACH中,∠ACH=45°,
∴AH=CH=BD.
∴AB=AH+BH=BD+0.5.
∵EF⊥FB,AB⊥FB,
∴∠EFG=∠ABG=90°.
由反射角等于入射角,得∠EGF=∠AGB.
∴△EFG∽△ABG.
∴.
∴.
解得BD=17.5.
∴AB=17.5+0.5=18(m).
∴这棵古树的高AB为18 m.
4.C 解析:∵AB∥A'B',
∴△ABO∽△A'B'O.
∴.
∴.
∴AB=24 mm.
∴物体AB的宽是24 mm.故选C.
5.解:如图,过点E作EG⊥BC于点G,
∵DE∥BC,∴△ABC∽△ADE.
∴.
∴.
∵AF⊥BC,EG⊥BC.
∴AF∥EG.
∴△ACF∽△ECG.
∴,即.
解得AF=90.
∴桥AF的长度为90 m.
课后提升
1.B 解析:由题意,得AB⊥BD,CD⊥BD.
∴∠ABE=∠CDE=90°.
由光的反射原理,得∠AEB=∠CED.
∴△AEB∽△CED.
∴.
∵BE=8 m,DE=4 m,CD=1.6 m,
∴.
∴AB=3.2 m.故选B.
2.A 解析:由题意,得AD∥BE,则∠CFD=∠AFB=∠CBE,△CDF∽△CEB.
∵∠CEB=∠ABF=90°,∠CBE=∠AFB,
∴△CBE∽△AFB.
∴.
∵BC=2.6 m,BE=1 m,
∴CE==2.4 m.
∴.
解得FB=,AF=.
∵△CDF∽△CEB,
∴,
即.
解得DF=.
∴AD=AF+DF==2.2(m).
∴此时点A离地面的距离为2.2 m.
故选A.
3.解:如图,延长AF,交DE于点G.
∵BC∥DE,
∴△ABC∽△ADE,AG⊥ED.
∴.
又∵BC=10 m,AF=3 m,FG=12 m,
∴AG=AF+FG=15 m.
∴.
∴DE=50 m.
∴50÷2+1=26(棵).
∴宣传栏后DE处共有26棵树.
4.解:如图,过点E作EG⊥CF于点G,延长GE交AD于点H,则GH⊥AD.
∵CF⊥AC,AD⊥AC,BE⊥AC,
∴四边形CBEG,四边形AHEB是矩形.
∴AH=BE=CG=1.5 m,BC=EG=9.5-0.3=9.2(m),AB=HE=0.3 m.
∵∠FGE=∠EHD=∠FED=90°,
∴∠EFG+∠FEG=∠FEG+∠DEH=90°.
∴∠EFG=∠DEH.
∴△EFG∽△DEH.
∴.
∴.
∴DH=9.2 m.
∴AD=DH+AH=9.2+1.5=10.7(m).
∴树的高度AD为10.7 m.
5.解:(1)由题意,得FC∥DE.
∴△BFC∽△BED.
∴.
∴.
∴BC=3 m.
∴BC的长为3 m.
(2)∵AC=5.4 m.
∴AB=5.4-3=2.4(m).
∵光在镜面反射中的反射角等于入射角,
∴∠GBA=∠FBC.
又∵∠GAB=∠FCB,
∴△BGA∽△BFC.
∴.
∴.
∴AG=1.2 m.
∴灯泡到地面的高度AG为1.2 m.
