第二十八章 锐角三角函数 评估测试卷(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 第二十八章 锐角三角函数 评估测试卷(含答案) 2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 269.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 00:00:00 | ||
图片预览




文档简介
第二十八章 锐角三角函数 评估测试卷
(满分:120分 时间:120分钟)
一、选择题(共12题,每题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.sin 30°+tan 60°cos 45°的值是 ( )
A. B.
C. D.
2.在Rt△ABC中,∠C=90°,若AC=3,AB=5,则∠B的正切值为 ( )
A. B. C. D.
3.如图,在△ABC中,∠C=90°,AC=5.若cos A=,则BC的长为 ( )
A.8 B.12 C.13 D.18
4.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=6.若用科学计算器求边AC的长,则下列按键顺序正确的是 ( )
A. B.
C. D.
5.如图,甲、乙两艘轮船从某港口O同时出发,各自沿一固定方向航行,其中甲航行方向为北偏西60°,乙航行方向为北偏东30°,甲每小时航行12 n mile,乙每小时航行16 n mile,他们离开港口2 h后分别位于点A,B处,则此时两船相距 ( )
A.36 n mile B.40 n mile
C.48 n mile D.50 n mile
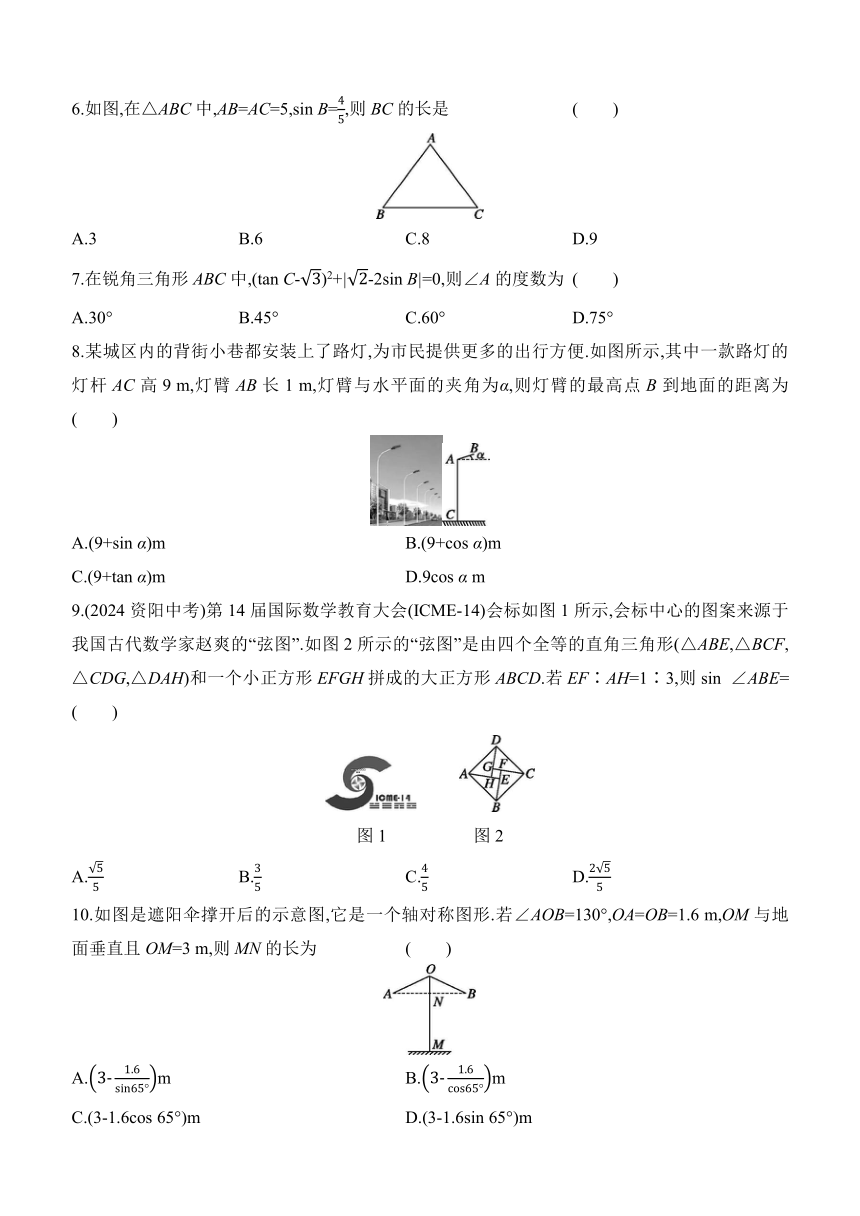
6.如图,在△ABC中,AB=AC=5,sin B=,则BC的长是 ( )
A.3 B.6 C.8 D.9
7.在锐角三角形ABC中,(tan C-)2+|-2sin B|=0,则∠A的度数为 ( )
A.30° B.45° C.60° D.75°
8.某城区内的背街小巷都安装上了路灯,为市民提供更多的出行方便.如图所示,其中一款路灯的灯杆AC高9 m,灯臂AB长1 m,灯臂与水平面的夹角为α,则灯臂的最高点B到地面的距离为 ( )
A.(9+sin α)m B.(9+cos α)m
C.(9+tan α)m D.9cos α m
9.(2024资阳中考)第14届国际数学教育大会(ICME-14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF∶AH=1∶3,则sin ∠ABE= ( )
图1 图2
A. B. C. D.
10.如图是遮阳伞撑开后的示意图,它是一个轴对称图形.若∠AOB=130°,OA=OB=1.6 m,OM与地面垂直且OM=3 m,则MN的长为 ( )
A.m B.m
C.(3-1.6cos 65°)m D.(3-1.6sin 65°)m
11.(2024德阳中考)如图,某校学生开展综合实践活动,测量一建筑物CD的高度,在建筑物旁边有一高度为10 m的小楼房AB,小李同学在小楼房楼底B处测得C处的仰角为60°,在小楼房楼顶A处测得C处的仰角为30°(AB,CD在同一平面内,点B,D在同一水平面上),则建筑物CD的高为 ( )
A.20 m B.15 m
C.12 m D.(10+5)m
12.(2024深圳中考)如图,为了测量某电子厂的高度,小明用高1.8 m的测量仪EF测得顶端A的仰角为45°,小军在小明的前面5 m处用高1.5 m的测量仪CD测得顶端A的仰角为53°,则电子厂AB的高度为( )
A.22.7 m B.22.4 m C.21.2 m D.23.0 m
二、填空题(共4题,每题3分,共12分)
13.若cos A=,则锐角∠A= .
14.计算:-2cos 30°+|-|-(4-π)0= .
15.(2024盐城中考)如图,小明用无人机测量教学楼的高度,将无人机垂直上升至距地面30 m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6 m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 m.(精确到1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
16.(2024湖南中考)如图,图1为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”的结构简图,图2为其平面示意图.已知AB⊥CD于点B,AB与水平线l相交于点O,OE⊥l.若BC=4 dm,OB=12 dm,∠BOE=60°,则点C到水平线l的距离CF为 dm.(结果用含根号的式子表示)
图1 图2
三、解答题(共8题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)计算:
(1)sin230°+2sin 60°+tan 45°+cos230°.
(2)-2sin 45°+2cos 60°+|1-|+.
18.(8分)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)已知c=2,b=,求∠B的度数.
(2)已知c=12,sin A=,求b的长.
19.(8分)(2024浙江中考)如图,在△ABC中,AD⊥BC,AE是BC边上的中线,AB=10,AD=6,tan∠ACB=1.
(1)求BC的长.
(2)求sin∠DAE的值.
20.(8分)如图,AB为☉O的直径,C为☉O上的一点,OD⊥AB交AC于点E,DE=DC.
(1)求证:DC是☉O的切线.
(2)若OA=4,OE=2,求cos D.
21.(10分)(2024天津中考)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔AB的高度(如图1).某学习小组设计了一个方案:如图2,点C,D,E依次在同一条水平直线上,DE=36 m,EC⊥AB,垂足为C.在D处测得桥塔顶部B的仰角(∠CDB)为45°,测得桥塔底部A的俯角(∠CDA)为6°,又在E处测得桥塔顶部B的仰角(∠CEB)为31°.
(1)求线段CD的长.
(2)求桥塔AB的高度.
(结果取整数,参考数据:tan 31°≈0.6,tan 6°≈0.1)
图1 图2
22.(10分)(2024张家口宣化区期末)如图,已知四边形ABCD内接于☉O,C是的中点,FC⊥AC于点C,与☉O及AD的延长线分别交于点E,F,且.
(1)求证:△CBA∽△FDC.
(2)如果AC=9,AB=4,求tan∠ACB的值.
23.(10分)(2024资阳中考)如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东30°方向,且A,B相距 n mile.一渔船在C处捕鱼,测得C处在灯塔A的北偏东30°方向、灯塔B的正北方向.
(1)求B,C两处的距离.
(2)该渔船从C处沿北偏东65°方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东27°方向,便立即以18 n mile/h的速度沿BD方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:tan 65°≈2.1,tan 27°≈0.5)
24.(10分)(2024广东中考)中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,∠ABQ=60°,AB=5.4 m,CE=1.6 m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1 m,参考数据:≈1.73)
(1)求PQ的长.
(2)该充电站有20个停车位,求PN的长.
【详解答案】
1.C 解析:sin 30°+tan 60°cos 45°=.故选C.
2.A 解析:在Rt△ABC中,∠C=90°,AC=3,AB=5,则BC==4,∴tan B=.故选A.
3.B 解析:∵在△ABC中,∠C=90°,AC=5,cos A=,∴.∴AB=13.∴BC==12.故选B.
4.D 解析:在Rt△ABC中,∵tan∠ABC=,∴AC=BC·tan∠ABC=6×tan 26°.故选D.
5.B 解析:由题意可知∠AOB=60°+30°=90°,∵甲每小时航行12 n mile,乙每小时航行16 n mile,航行2 h,∴OA=24 n mile,OB=32 n mile.∴AB==40(n mile).则此时两船相距40 n mile.故选B.
6.B 解析:如图,过点A作BC的垂线,垂足为M,
在Rt△ABM中,sin B=,∴AM=5×=4.∴BM==3.又∵AB=AC,∴BC=2BM=6.故选B.
7.D 解析:∵(tan C-)2+|-2sin B|=0,∴tan C=,sin B=.∴∠C=60°,∠B=45°.∴∠A=75°.故选D.
8.A 解析:如图,过点B作BE⊥AD,垂足为E,延长BE交CF于点G,
由题意,得AC=EG=9 m,BG⊥CF,在Rt△ABE中,AB=1 m,∠BAE=α,∴BE=AB·sin α=sin α(m).∴BG=BE+EG=(sin α+9)m,∴灯臂的最高点B到地面的距离为(9+sin α)m.故选A.
9.C 解析:根据题意,设EF=x,则AH=3x,∵△ABE≌△DAH,四边形EFGH为正方形,∴AH=BE=3x,EF=HE=x.∴AE=4x.∵∠AEB=90°,∴AB==5x.∴sin∠ABE=.故选C.
10.C 解析:∵∠AOB=130°,OA=OB=1.6 m,整个图形是一个轴对称图形,∴ON⊥AB,∠AON=∠AOB=65°.在Rt△AON中,ON=OA·cos∠AON=1.6cos 65° m,∵OM=3 m,∴MN=OM-ON=(3-1.6 cos 65°)m.故选C.
11.B 解析:如图,设过点A的水平线与CD交于点E,
由题意,知四边形ABDE是矩形,DE=AB=10 m,AE=BD,在Rt△BCD中,BD=CD.在Rt△ACE中,AE=(CD-DE)=(CD-10).∴(CD-10)=CD.解得CD=15 m.故选B.
12.A 解析:由题意,得EF=BM=1.8 m,CD=BN=1.5 m,DF=5 m,EM=BF,BD=CN,EM⊥AB,CN⊥AB,设BD=CN=x m,∴EM=BF=DF+BD=(x+5)m.在Rt△AEM中,∠AEM=45°,∴AM=EM·tan 45°=(x+5)m.在Rt△ACN中,∠ACN=53°,∴AN=CN·tan 53°≈x m.∵AM+BM=AN+BN=AB,∴x+5+1.8=x+1.5.解得x=15.9.∴AN=21.2 m.∴AB=AN+BN=21.2+1.5=22.7(m).∴电子厂AB的高度约为22.7 m.故选A.
13.60° 解析:∵cos A=,∴锐角∠A=60°.
14.2 解析:原式=3-2×-1=3--1=2.
15.17 解析:如图,令AB的延长线与PQ的延长线交于点C,
由题意,知AC=30 m,PQ=26.6 m,∠APC=37°,∠BQC=45°,在Rt△APC中,PC=≈=40(m).∴QC=PC-PQ=40-26.6=13.4(m).在Rt△BQC中,BC=QC=13.4 m,∴AB=AC-BC=30-13.4=16.6≈17(m).
16.(6-2) 解析:如图,延长DC交l于点H,连接OC,在Rt△OBH中,∠BOH=90°-60°=30°,OB=12 dm,∴BH=12×tan 30°=4(dm),OH=2BH=8 dm.∵S△OBH=S△OCH+S△OBC,∴OB·BH=OH·CF+OB·BC.∴×12×4×8×CF+×12×4.∴CF=(6-2)dm.
17.解:(1)原式=sin230°+cos230°+2sin 60°+tan 45°
=+2×+1
=2+.
(2)原式=2-2×+2×-1+2
=2+1+-1+2
=2+2.
18.解:(1)∵sin B=,
∴∠B=45°.
(2)∵c=12,sin A=,
∴a=4,
∴b==8.
19.解:(1)∵AD⊥BC,AB=10,AD=6,
∴BD==8.
∵tan∠ACB=1,∴CD=AD=6.
∴BC=BD+CD=8+6=14.
(2)∵AE是BC边上的中线,
∴CE=BC=7.
∴DE=CE-CD=7-6=1.
∵AD⊥BC,
∴AE=.
∴sin∠DAE=.
20.解:(1)证明:如图,连接OC,
∵DE=DC,
∴∠DEC=∠DCE.
∵∠DEC=∠AEO,
∴∠DCE=∠AEO.
∵DO⊥AB,
∴∠AOD=90°.
∴∠EAO+∠AEO=∠EAO+∠DCE=90°.
∵OA=OC,∴∠EAO=∠OCA.
∴∠OCA+∠DCE=∠DCO=90°.
∵OC是☉O的半径,
∴DC是☉O的切线.
(2)设CD=x,
则DE=x,DO=DE+OE=x+2,
在Rt△OCD中,OD2=OC2+CD2,
即(x+2)2=42+x2.解得x=3.
∴CD=3,OD=5.
∴cos D=.
21.解:(1)设CD=x m,∵DE=36 m,
∴CE=CD+DE=(x+36)m.
∵EC⊥AB,∴∠BCE=∠ACD=90°.
∵tan∠CDB=,∠CDB=45°,
∴BC=CD·tan∠CDB=x·tan 45°=x(m).
∵tan∠CEB=,∠CEB=31°,
∴BC=CE·tan∠CEB=(x+36)tan 31°(m).
∴x=(x+36)·tan 31°.
解得x=54.
答:线段CD的长约为54 m.
(2)∵tan∠CDA=,∠CDA=6°,
∴AC=CD·tan∠CDA=54×tan 6°≈54×0.1=5.4(m).
∴AB=AC+BC=5.4+54≈59(m).
答:桥塔AB的高度约为59 m.
22.解:(1)证明:∵,
∴∠CAB=∠FCD.
∵四边形ABCD内接于☉O,
∴∠ABC=∠FDC.
∴△CBA∽△FDC.
(2)∵C是的中点,
∴.∴DC=AC=9.
∵△CBA∽△FDC,
∴.∴.
∴FC=.
∵△CBA∽△FDC,
∴∠ACB=∠CFD.
∵FC⊥AC,
∴tan∠CFA=.
∴tan∠ACB=tan∠CFA=.
23.解:(1)由题意,得∠ACB=∠ABC=30°,
∴AB=AC= n mile.
如图,过点A作AH⊥BC于点H,
∴∠AHC=∠AHB=90°,CH=BH.
∴CH=BH=AB·cos 30°==8(n mile).
∴BC=16 n mile.
答:B,C两处的距离为16 n mile.
(2)如图,过点D作DG⊥BC交BC的延长线于点G,
在Rt△BDG中,BG=≈=2DG,
在Rt△CDG中,CG=≈,
∵BC=BG-CG,∴2DG-=16.
∴DG=10.5 n mile.
∴CG=5 n mile.
∴BG=BC+CG=21 n mile.
∴BD= n mile.
∴÷18=(h).
答:渔政船的航行时间为 h.
24.解:(1)∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
在Rt△ABQ中,∠ABQ=60°,AB=5.4 m,
∴AQ=AB·sin∠ABQ= m,
∠QAB=30°.
∵四边形ABCD是矩形,
∴AD=BC,∠BAD=∠BCD=∠ABC=∠BCE=90°.
∴∠CBE=30°.
∴BC= m,
∴AD= m.
∵∠PAD=180°-30°-90°=60°,
∴AP=AD·cos∠PAD= m.
∴PQ=AP+AQ=≈6.1 m.
(2)在Rt△BCE中,BE==3.2 m.
在Rt△ABQ中,BQ=AB·cos∠ABQ=2.7 m.
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7 m.
∵四边形PQMN是矩形,
∴PN=QM=66.7 m.
(满分:120分 时间:120分钟)
一、选择题(共12题,每题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.sin 30°+tan 60°cos 45°的值是 ( )
A. B.
C. D.
2.在Rt△ABC中,∠C=90°,若AC=3,AB=5,则∠B的正切值为 ( )
A. B. C. D.
3.如图,在△ABC中,∠C=90°,AC=5.若cos A=,则BC的长为 ( )
A.8 B.12 C.13 D.18
4.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=6.若用科学计算器求边AC的长,则下列按键顺序正确的是 ( )
A. B.
C. D.
5.如图,甲、乙两艘轮船从某港口O同时出发,各自沿一固定方向航行,其中甲航行方向为北偏西60°,乙航行方向为北偏东30°,甲每小时航行12 n mile,乙每小时航行16 n mile,他们离开港口2 h后分别位于点A,B处,则此时两船相距 ( )
A.36 n mile B.40 n mile
C.48 n mile D.50 n mile
6.如图,在△ABC中,AB=AC=5,sin B=,则BC的长是 ( )
A.3 B.6 C.8 D.9
7.在锐角三角形ABC中,(tan C-)2+|-2sin B|=0,则∠A的度数为 ( )
A.30° B.45° C.60° D.75°
8.某城区内的背街小巷都安装上了路灯,为市民提供更多的出行方便.如图所示,其中一款路灯的灯杆AC高9 m,灯臂AB长1 m,灯臂与水平面的夹角为α,则灯臂的最高点B到地面的距离为 ( )
A.(9+sin α)m B.(9+cos α)m
C.(9+tan α)m D.9cos α m
9.(2024资阳中考)第14届国际数学教育大会(ICME-14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF∶AH=1∶3,则sin ∠ABE= ( )
图1 图2
A. B. C. D.
10.如图是遮阳伞撑开后的示意图,它是一个轴对称图形.若∠AOB=130°,OA=OB=1.6 m,OM与地面垂直且OM=3 m,则MN的长为 ( )
A.m B.m
C.(3-1.6cos 65°)m D.(3-1.6sin 65°)m
11.(2024德阳中考)如图,某校学生开展综合实践活动,测量一建筑物CD的高度,在建筑物旁边有一高度为10 m的小楼房AB,小李同学在小楼房楼底B处测得C处的仰角为60°,在小楼房楼顶A处测得C处的仰角为30°(AB,CD在同一平面内,点B,D在同一水平面上),则建筑物CD的高为 ( )
A.20 m B.15 m
C.12 m D.(10+5)m
12.(2024深圳中考)如图,为了测量某电子厂的高度,小明用高1.8 m的测量仪EF测得顶端A的仰角为45°,小军在小明的前面5 m处用高1.5 m的测量仪CD测得顶端A的仰角为53°,则电子厂AB的高度为( )
A.22.7 m B.22.4 m C.21.2 m D.23.0 m
二、填空题(共4题,每题3分,共12分)
13.若cos A=,则锐角∠A= .
14.计算:-2cos 30°+|-|-(4-π)0= .
15.(2024盐城中考)如图,小明用无人机测量教学楼的高度,将无人机垂直上升至距地面30 m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6 m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 m.(精确到1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
16.(2024湖南中考)如图,图1为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”的结构简图,图2为其平面示意图.已知AB⊥CD于点B,AB与水平线l相交于点O,OE⊥l.若BC=4 dm,OB=12 dm,∠BOE=60°,则点C到水平线l的距离CF为 dm.(结果用含根号的式子表示)
图1 图2
三、解答题(共8题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)计算:
(1)sin230°+2sin 60°+tan 45°+cos230°.
(2)-2sin 45°+2cos 60°+|1-|+.
18.(8分)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)已知c=2,b=,求∠B的度数.
(2)已知c=12,sin A=,求b的长.
19.(8分)(2024浙江中考)如图,在△ABC中,AD⊥BC,AE是BC边上的中线,AB=10,AD=6,tan∠ACB=1.
(1)求BC的长.
(2)求sin∠DAE的值.
20.(8分)如图,AB为☉O的直径,C为☉O上的一点,OD⊥AB交AC于点E,DE=DC.
(1)求证:DC是☉O的切线.
(2)若OA=4,OE=2,求cos D.
21.(10分)(2024天津中考)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔AB的高度(如图1).某学习小组设计了一个方案:如图2,点C,D,E依次在同一条水平直线上,DE=36 m,EC⊥AB,垂足为C.在D处测得桥塔顶部B的仰角(∠CDB)为45°,测得桥塔底部A的俯角(∠CDA)为6°,又在E处测得桥塔顶部B的仰角(∠CEB)为31°.
(1)求线段CD的长.
(2)求桥塔AB的高度.
(结果取整数,参考数据:tan 31°≈0.6,tan 6°≈0.1)
图1 图2
22.(10分)(2024张家口宣化区期末)如图,已知四边形ABCD内接于☉O,C是的中点,FC⊥AC于点C,与☉O及AD的延长线分别交于点E,F,且.
(1)求证:△CBA∽△FDC.
(2)如果AC=9,AB=4,求tan∠ACB的值.
23.(10分)(2024资阳中考)如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东30°方向,且A,B相距 n mile.一渔船在C处捕鱼,测得C处在灯塔A的北偏东30°方向、灯塔B的正北方向.
(1)求B,C两处的距离.
(2)该渔船从C处沿北偏东65°方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东27°方向,便立即以18 n mile/h的速度沿BD方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:tan 65°≈2.1,tan 27°≈0.5)
24.(10分)(2024广东中考)中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,∠ABQ=60°,AB=5.4 m,CE=1.6 m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1 m,参考数据:≈1.73)
(1)求PQ的长.
(2)该充电站有20个停车位,求PN的长.
【详解答案】
1.C 解析:sin 30°+tan 60°cos 45°=.故选C.
2.A 解析:在Rt△ABC中,∠C=90°,AC=3,AB=5,则BC==4,∴tan B=.故选A.
3.B 解析:∵在△ABC中,∠C=90°,AC=5,cos A=,∴.∴AB=13.∴BC==12.故选B.
4.D 解析:在Rt△ABC中,∵tan∠ABC=,∴AC=BC·tan∠ABC=6×tan 26°.故选D.
5.B 解析:由题意可知∠AOB=60°+30°=90°,∵甲每小时航行12 n mile,乙每小时航行16 n mile,航行2 h,∴OA=24 n mile,OB=32 n mile.∴AB==40(n mile).则此时两船相距40 n mile.故选B.
6.B 解析:如图,过点A作BC的垂线,垂足为M,
在Rt△ABM中,sin B=,∴AM=5×=4.∴BM==3.又∵AB=AC,∴BC=2BM=6.故选B.
7.D 解析:∵(tan C-)2+|-2sin B|=0,∴tan C=,sin B=.∴∠C=60°,∠B=45°.∴∠A=75°.故选D.
8.A 解析:如图,过点B作BE⊥AD,垂足为E,延长BE交CF于点G,
由题意,得AC=EG=9 m,BG⊥CF,在Rt△ABE中,AB=1 m,∠BAE=α,∴BE=AB·sin α=sin α(m).∴BG=BE+EG=(sin α+9)m,∴灯臂的最高点B到地面的距离为(9+sin α)m.故选A.
9.C 解析:根据题意,设EF=x,则AH=3x,∵△ABE≌△DAH,四边形EFGH为正方形,∴AH=BE=3x,EF=HE=x.∴AE=4x.∵∠AEB=90°,∴AB==5x.∴sin∠ABE=.故选C.
10.C 解析:∵∠AOB=130°,OA=OB=1.6 m,整个图形是一个轴对称图形,∴ON⊥AB,∠AON=∠AOB=65°.在Rt△AON中,ON=OA·cos∠AON=1.6cos 65° m,∵OM=3 m,∴MN=OM-ON=(3-1.6 cos 65°)m.故选C.
11.B 解析:如图,设过点A的水平线与CD交于点E,
由题意,知四边形ABDE是矩形,DE=AB=10 m,AE=BD,在Rt△BCD中,BD=CD.在Rt△ACE中,AE=(CD-DE)=(CD-10).∴(CD-10)=CD.解得CD=15 m.故选B.
12.A 解析:由题意,得EF=BM=1.8 m,CD=BN=1.5 m,DF=5 m,EM=BF,BD=CN,EM⊥AB,CN⊥AB,设BD=CN=x m,∴EM=BF=DF+BD=(x+5)m.在Rt△AEM中,∠AEM=45°,∴AM=EM·tan 45°=(x+5)m.在Rt△ACN中,∠ACN=53°,∴AN=CN·tan 53°≈x m.∵AM+BM=AN+BN=AB,∴x+5+1.8=x+1.5.解得x=15.9.∴AN=21.2 m.∴AB=AN+BN=21.2+1.5=22.7(m).∴电子厂AB的高度约为22.7 m.故选A.
13.60° 解析:∵cos A=,∴锐角∠A=60°.
14.2 解析:原式=3-2×-1=3--1=2.
15.17 解析:如图,令AB的延长线与PQ的延长线交于点C,
由题意,知AC=30 m,PQ=26.6 m,∠APC=37°,∠BQC=45°,在Rt△APC中,PC=≈=40(m).∴QC=PC-PQ=40-26.6=13.4(m).在Rt△BQC中,BC=QC=13.4 m,∴AB=AC-BC=30-13.4=16.6≈17(m).
16.(6-2) 解析:如图,延长DC交l于点H,连接OC,在Rt△OBH中,∠BOH=90°-60°=30°,OB=12 dm,∴BH=12×tan 30°=4(dm),OH=2BH=8 dm.∵S△OBH=S△OCH+S△OBC,∴OB·BH=OH·CF+OB·BC.∴×12×4×8×CF+×12×4.∴CF=(6-2)dm.
17.解:(1)原式=sin230°+cos230°+2sin 60°+tan 45°
=+2×+1
=2+.
(2)原式=2-2×+2×-1+2
=2+1+-1+2
=2+2.
18.解:(1)∵sin B=,
∴∠B=45°.
(2)∵c=12,sin A=,
∴a=4,
∴b==8.
19.解:(1)∵AD⊥BC,AB=10,AD=6,
∴BD==8.
∵tan∠ACB=1,∴CD=AD=6.
∴BC=BD+CD=8+6=14.
(2)∵AE是BC边上的中线,
∴CE=BC=7.
∴DE=CE-CD=7-6=1.
∵AD⊥BC,
∴AE=.
∴sin∠DAE=.
20.解:(1)证明:如图,连接OC,
∵DE=DC,
∴∠DEC=∠DCE.
∵∠DEC=∠AEO,
∴∠DCE=∠AEO.
∵DO⊥AB,
∴∠AOD=90°.
∴∠EAO+∠AEO=∠EAO+∠DCE=90°.
∵OA=OC,∴∠EAO=∠OCA.
∴∠OCA+∠DCE=∠DCO=90°.
∵OC是☉O的半径,
∴DC是☉O的切线.
(2)设CD=x,
则DE=x,DO=DE+OE=x+2,
在Rt△OCD中,OD2=OC2+CD2,
即(x+2)2=42+x2.解得x=3.
∴CD=3,OD=5.
∴cos D=.
21.解:(1)设CD=x m,∵DE=36 m,
∴CE=CD+DE=(x+36)m.
∵EC⊥AB,∴∠BCE=∠ACD=90°.
∵tan∠CDB=,∠CDB=45°,
∴BC=CD·tan∠CDB=x·tan 45°=x(m).
∵tan∠CEB=,∠CEB=31°,
∴BC=CE·tan∠CEB=(x+36)tan 31°(m).
∴x=(x+36)·tan 31°.
解得x=54.
答:线段CD的长约为54 m.
(2)∵tan∠CDA=,∠CDA=6°,
∴AC=CD·tan∠CDA=54×tan 6°≈54×0.1=5.4(m).
∴AB=AC+BC=5.4+54≈59(m).
答:桥塔AB的高度约为59 m.
22.解:(1)证明:∵,
∴∠CAB=∠FCD.
∵四边形ABCD内接于☉O,
∴∠ABC=∠FDC.
∴△CBA∽△FDC.
(2)∵C是的中点,
∴.∴DC=AC=9.
∵△CBA∽△FDC,
∴.∴.
∴FC=.
∵△CBA∽△FDC,
∴∠ACB=∠CFD.
∵FC⊥AC,
∴tan∠CFA=.
∴tan∠ACB=tan∠CFA=.
23.解:(1)由题意,得∠ACB=∠ABC=30°,
∴AB=AC= n mile.
如图,过点A作AH⊥BC于点H,
∴∠AHC=∠AHB=90°,CH=BH.
∴CH=BH=AB·cos 30°==8(n mile).
∴BC=16 n mile.
答:B,C两处的距离为16 n mile.
(2)如图,过点D作DG⊥BC交BC的延长线于点G,
在Rt△BDG中,BG=≈=2DG,
在Rt△CDG中,CG=≈,
∵BC=BG-CG,∴2DG-=16.
∴DG=10.5 n mile.
∴CG=5 n mile.
∴BG=BC+CG=21 n mile.
∴BD= n mile.
∴÷18=(h).
答:渔政船的航行时间为 h.
24.解:(1)∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
在Rt△ABQ中,∠ABQ=60°,AB=5.4 m,
∴AQ=AB·sin∠ABQ= m,
∠QAB=30°.
∵四边形ABCD是矩形,
∴AD=BC,∠BAD=∠BCD=∠ABC=∠BCE=90°.
∴∠CBE=30°.
∴BC= m,
∴AD= m.
∵∠PAD=180°-30°-90°=60°,
∴AP=AD·cos∠PAD= m.
∴PQ=AP+AQ=≈6.1 m.
(2)在Rt△BCE中,BE==3.2 m.
在Rt△ABQ中,BQ=AB·cos∠ABQ=2.7 m.
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7 m.
∵四边形PQMN是矩形,
∴PN=QM=66.7 m.
