第二十六章 反比例函数 评估测试卷(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 第二十六章 反比例函数 评估测试卷(含答案) 2024-2025学年数学人教版九年级下册 | 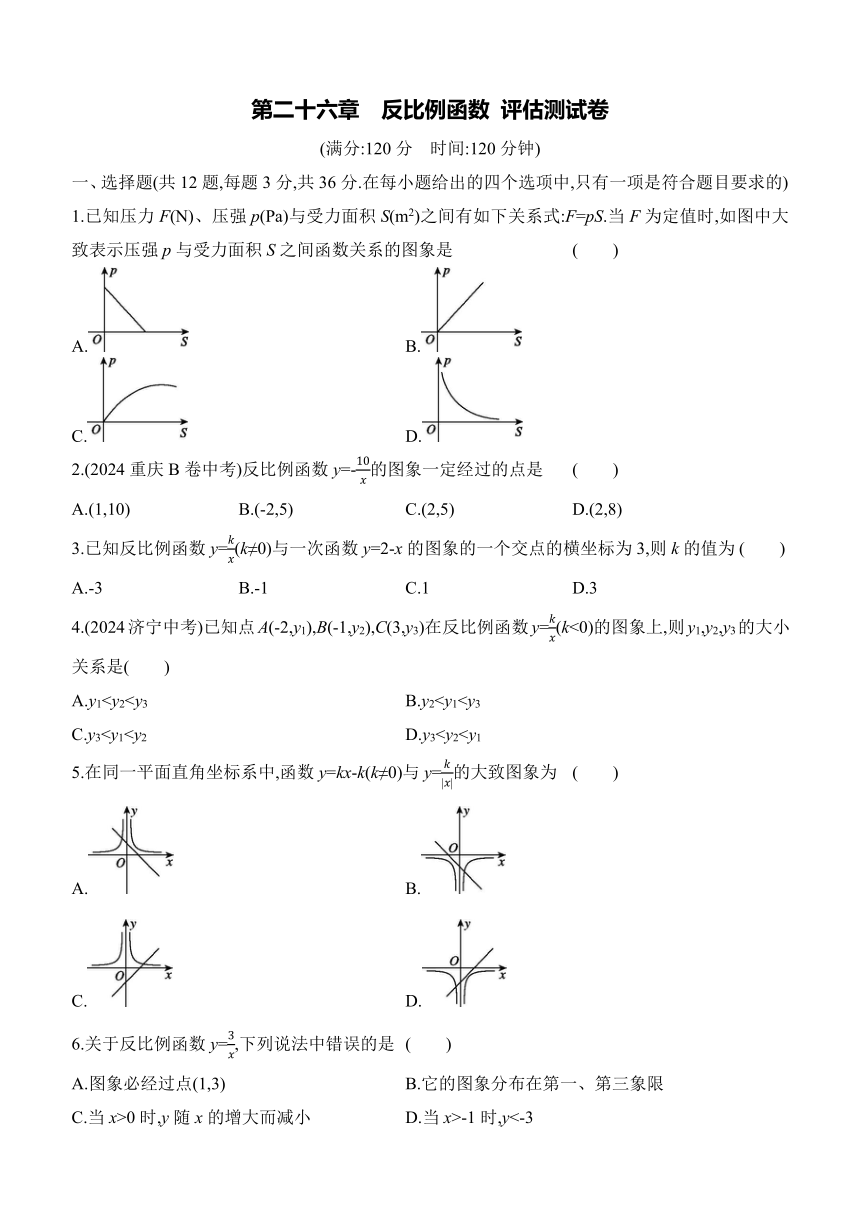 | |
| 格式 | docx | ||
| 文件大小 | 268.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 21:20:29 | ||
图片预览




文档简介
第二十六章 反比例函数 评估测试卷
(满分:120分 时间:120分钟)
一、选择题(共12题,每题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知压力F(N)、压强p(Pa)与受力面积S(m2)之间有如下关系式:F=pS.当F为定值时,如图中大致表示压强p与受力面积S之间函数关系的图象是 ( )
A. B.
C. D.
2.(2024重庆B卷中考)反比例函数y=-的图象一定经过的点是 ( )
A.(1,10) B.(-2,5) C.(2,5) D.(2,8)
3.已知反比例函数y=(k≠0)与一次函数y=2-x的图象的一个交点的横坐标为3,则k的值为 ( )
A.-3 B.-1 C.1 D.3
4.(2024济宁中考)已知点A(-2,y1),B(-1,y2),C(3,y3)在反比例函数y=(k<0)的图象上,则y1,y2,y3的大小关系是( )
A.y1C.y35.在同一平面直角坐标系中,函数y=kx-k(k≠0)与y=的大致图象为 ( )
A. B.
C. D.
6.关于反比例函数y=,下列说法中错误的是 ( )
A.图象必经过点(1,3) B.它的图象分布在第一、第三象限
C.当x>0时,y随x的增大而减小 D.当x>-1时,y<-3
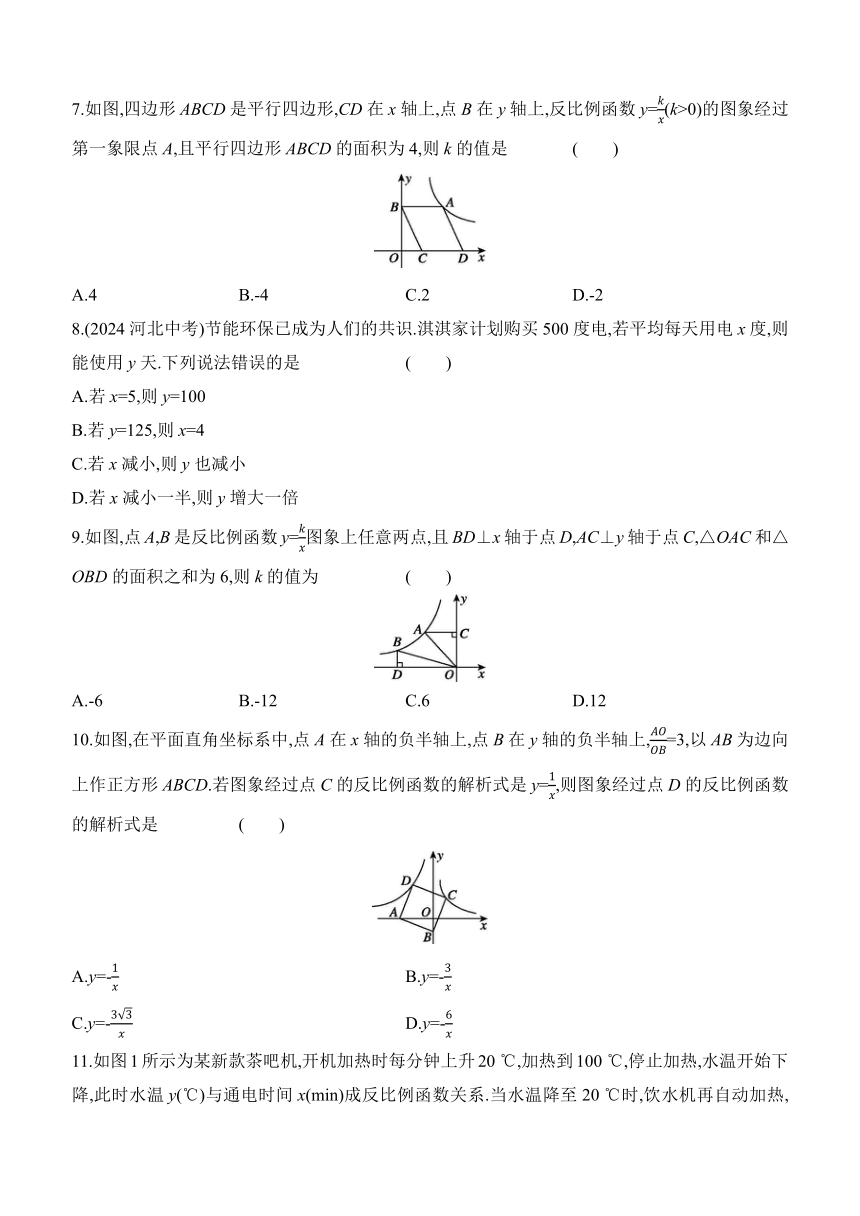
7.如图,四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数y=(k>0)的图象经过第一象限点A,且平行四边形ABCD的面积为4,则k的值是 ( )
A.4 B.-4 C.2 D.-2
8.(2024河北中考)节能环保已成为人们的共识.淇淇家计划购买500度电,若平均每天用电x度,则能使用y天.下列说法错误的是 ( )
A.若x=5,则y=100
B.若y=125,则x=4
C.若x减小,则y也减小
D.若x减小一半,则y增大一倍
9.如图,点A,B是反比例函数y=图象上任意两点,且BD⊥x轴于点D,AC⊥y轴于点C,△OAC和△OBD的面积之和为6,则k的值为 ( )
A.-6 B.-12 C.6 D.12
10.如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在y轴的负半轴上,=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y=,则图象经过点D的反比例函数的解析式是 ( )
A.y=- B.y=-
C.y=- D.y=-
11.如图1所示为某新款茶吧机,开机加热时每分钟上升20 ℃,加热到100 ℃,停止加热,水温开始下降,此时水温y(℃)与通电时间x(min)成反比例函数关系.当水温降至20 ℃时,饮水机再自动加热,若水温在20 ℃时接通电源,水温y(℃)与通电时间x(min)之间的关系如图2所示,则下列说法中错误的是 ( )
图1 图2
A.水温从20 ℃加热到100 ℃,需要4 min
B.水温下降过程中,y与x的函数解析式是y=
C.上午10:00接通电源,可以保证当天10:30能喝到不低于38 ℃的水
D.在一个加热周期内水温不低于40 ℃的时间为7 min
12.(2024长沙模拟)如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一个分支上,分别过点A,C作x轴的垂线段,垂足分别为M和N,给出如下四个结论:①;②阴影部分的面积是(k1+k2);③当∠AOC= 90°时,|k1|=|k2|;④若OABC是菱形,则k1+k2=0.其中正确的是 ( )
A.①③ B.①②③
C.②③④ D.①④
二、填空题(共4题,每题3分,共12分)
13.某反比例函数y=具有下列性质:当x>0时,y随x的增大而减小.写出一个满足条件的k的值是 .
14.(2024山西中考)如图所示的机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数.已知一款机器狗载重后总质量m=60 kg时,它的最快移动速度v=6 m/s;当其载重后总质量m=90 kg时,它的最快移动速度v= m/s.
15.为预防传染病,某校定期对教室进行“药熏消毒”.如图所示,药物燃烧阶段,教室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比例;燃烧后,y与x成反比例.若y>1.6,则x的取值范围是 .
16.如图, ABCO的顶点B在双曲线y=上,顶点C在双曲线y=上,BC的中点P恰好落在y轴上.已知S OABC=10,则k= .
三、解答题(共8题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)已知反比例函数y=.
(1)画出反比例函数的图象.
(2)观察图象,直接写出当y≥-1时,x的取值范围.
18.(6分)(2024吉林二模)小明家购买一套商品房,首付45万元,剩余部分需贷款并按“等额本息”的形式偿还,即贷款金额按月分期还款,且每月偿还贷款金额数相同.若设每月偿还贷款金额y万元,x个月还清,且y是x的反比例函数,其图象如图所示.
(1)求y与x的函数解析式.
(2)若小明家计划每月偿还贷款金额不超过3 000元,则至少需要多少个月还清
19.(6分)如图,点A(a,b),B(4,1)在反比例函数y=的图象上,过点O,B的直线交双曲线的另一支于点C.
(1)求反比例函数的解析式.
(2)连接AC,AB,若4a=b,求△ABC的面积.
20.(10分)大约在两千四五百年前,如图1,墨子和他的学生做了世界上第1个小孔成像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端.”如图2,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
(1)求y关于x的函数解析式.
(2)若小孔到蜡烛的距离为4 cm,求火焰的像高.
(3)若火焰的像高不得超过3 cm,则小孔到蜡烛的距离至少是多少厘米
图1 图2
21.(10分)如图,菱形OABC的顶点O为原点,点C在y轴上,点A的坐标为(4,3),反比例函数y=(k≠0)的图象经过点B.
(1)求k的值和直线AC的解析式.
(2)将直线AC沿y轴平移m个单位长度,当直线AC与反比例函数y=(k≠0)的图象只有一个交点时,求m的值.
22.(10分)(2024广元中考)如图,已知反比例函数y1=和一次函数y2=mx+n的图象相交于A(-3,a), B两点,O为坐标原点,连接OA,OB.
(1)求y1=与y2=mx+n的解析式.
(2)当y1>y2时,请结合图象直接写出自变量x的取值范围.
(3)求△AOB的面积.
23.(12分)(2024天津河东区一模)通过实验研究发现:初中生在数学课上听课注意力指标数随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标数y随时间x(min)变化的函数图象如图所示.当0≤x<10和10≤x<20时,图象是线段;当20≤x≤40时,图象是双曲线的一部分.根据函数图象回答下列问题:
(1)点A的注意力指标数是 .
(2)当0≤x<10时,求注意力指标数y关于时间x(min)的函数解析式.
(3)张老师在一节课上讲解一道数学综合题需要20 min,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36 请说明理由.
24.(12分)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=的图象交于点A(-1,a)与点B(m,-1).
(1)求这个一次函数的解析式.
(2)根据图象,直接写出不等式(3)动点P是x轴上的点,若△PAB的面积等于6,则点P的横坐标为 .
【详解答案】
1.D 解析:∵压力F(N)、压强p(Pa)与受力面积S(m2)之间有如下关系式:F=pS.∴当F为定值时,压强p与受力面积S之间的函数关系是反比例函数.故选D.
2.B 解析:当x=1时,y=-10,∴图象不经过点(1,10).故A选项错误;当x=-2时,y=5,∴图象经过点(-2,5).故B选项正确;当x=2时,y=-5,∴图象不经过点(2,5),(2,8).故C选项、D选项错误.故选B.
3.A 解析:将x=3代入y=2-x中,得y=-1.将点(3,-1)代入y=中,得k=-3.故选A.
4.C 解析:在反比例函数y=中k<0,反比例函数图象分布在第二、第四象限,在每个象限内,y随x的增大而增大,∵点C(3,y3)在第四象限,∴y3<0.∵-2<-1,∴05.C 解析:将x=1代入y=kx-k得,y=k-k=0,∴函数y=kx-k过定点(1,0).故B选项不符合题意.当k>0时,函数y=kx-k的图象经过第一、第三、第四象限.∵当k>0时,y=>0,∴此函数的图象都在x轴的上方.∴A、D不符合题意,C符合题意.故选C.
6.D 解析:∵反比例函数为y=,∴当x=1时,y=3.故A正确,不合题意.∵k=3>0,∴函数图象分布在第一、第三象限.故B正确,不合题意;当x>0时,y随x的增大而减小,故C正确,不合题意.∵x<0时,y随x的增大而减小,且当x=-1时,y=-3,∴当-17.A 解析:如图,连接OA,AC.∵四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,∴AB⊥y轴.∵S ABCD=4,∴S△ABC=2.∵AB∥OD,∴S△OAB=S△ABC=2.∴k=2S△OAB=2×2=4.故选A.
8.C 解析:由题意,得y=.A.若x=5,则y==100,正确,故此选项不符合题意;B.若y=125,则125=,解得x=4.正确,故此选项不符合题意;C.若x减小,则y增大,原说法错误,故此选项符合题意;D.若x减小一半,即y'=,∴y增大一倍.正确,故此选项不符合题意.故选C.
9.A 解析:∵点A,B是反比例函数图象上任意两点,∴设点A,B,∵BD⊥x轴于点D,AC⊥y轴于点C,∴BD=,OD=-b,OC=,AC=-a.∵△OAC和△OBD的面积之和为6,∴×OC·AC+BD·OD=··(-a)+··(-b)=-k-k=-k=6.∴k=-6.故选A.
10.B 解析:如图,过点C作CT⊥y轴于点T,过点D作DH⊥CT交CT的延长线于点H.∵=3,∴设OB=a,则OA=3a.∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠AOB=∠BTC=90°.∴∠ABO+∠CBT=90°,∠CBT+∠BCT=90°.∴∠ABO=∠BCT.∴△AOB≌△BTC(AAS).∴BT=AO=3a,TC=OB=a.∴OT=BT-OB=2a.∴点C(a,2a).∵点C在y=的图象上,∴2a2=1.同理可证△CHD≌△BTC.∴DH=CT=a,CH=BT=3a.∴点D(-2a,3a).设经过点D的反比例函数的解析式为y=,则有-2a×3a=k.∴k=-6a2=-3.∴经过点D的反比例函数的解析式是y=-.故选B.
11.D 解析:∵开机加热时每分钟上升20 ℃,∴水温从20 ℃加热到100 ℃,所需时间为=4(min).故A选项正确,不符合题意;设水温下降过程中,y与x的函数解析式为y=,由题意,得点(4,100)在反比例函数y=的图象上,∴100=.解得k=400.∴水温下降过程中,y与x的函数解析式是y=.故B选项正确,不符合题意;令y=20,则=20,∴x=20.∴从开机加热到水温降至20 ℃需要20 min,即一个循环为20 min,水温y(℃)与通电时间x(min)的函数解析式为
上午10:00到10:30共30 min,30-20=10(min),∴当x=10时,y==40,即此时的水温为40 ℃>38 ℃.故C选项正确,不符合题意;在加热过程中,水温为40 ℃时,20x+20=40,解得x=1.在降温过程中,水温为40 ℃时,40=,解得x=10.∵10-1=9(min),∴一个加热周期内水温不低于40 ℃的时间为9 min.故D选项错误,符合题意.故选D.
12.D 解析:如图,过点A作AE⊥y轴于点E,过点C作CF⊥y轴于点F.∵四边形OABC是平行四边形,∴S△AOB=S△COB.∵OB=OB,∴AE=CF.∴OM=ON.∵S△AOM=|k1|=OM·AM,S△CON=|k2|=ON·CN.∴.故①正确;∵S△AOM=|k1|,S△CON=|k2|,∴S阴影部分=S△AOM+S△CON=(|k1|+|k2|).而k1>0,k2<0,∴S阴影部分=(k1-k2).故②错误;当∠AOC=90°时,四边形OABC是矩形,∴不能确定OA与OC相等.而OM=ON,∴不能判断△AOM≌△CNO.∴不能判断AM=CN.∴不能确定|k1|=|k2|.故③错误;若四边形OABC是菱形,则OA=OC,而OM=ON,∴Rt△AOM≌Rt△CNO(HL).∴AM=CN.∴|k1|=|k2|.∴k1=-k2.∴k1+k2=0.故④正确.故选D.
13.1(答案不唯一) 解析:由题可知,反比例函数y=具有下列性质:当x>0时,y随x的增大而减小,∴k>0.则k的值可以取1.
14.4 解析:设反比例函数解析式为v=,∵机器狗载重后总质量m=60 kg时,它的最快移动速度v=6 m/s,∴k=60×6=360.∴反比例函数解析式为v=.当m=90 kg时,v==4(m/s),故当其载重后总质量m=90 kg时,它的最快移动速度v=4 m/s.
15.21.6时,x>1.6,解得x>2.当x>10时,设y与x的函数解析式为y=,把点(10,8)代入解析式,得m=80,∴y与x的函数解析式为y=.当y>1.6时,>1.6,解得x<50.∴y>1.6时,x的取值范围是216.-4 解析:如图,连接OB,过点B作BE⊥y轴于点E,过点C作CF⊥y轴于点F,则∠CFP=∠BEP=90°,∵P是BC的中点,∴CP=BP.又∵∠CPF=∠BPE,∴△CFP≌△BEP(AAS).∴S△BEP=S△CFP.∴S△OBC=S△OCF+S△CFP+S△OBP=S△OCF+S△BEP+S△OBP=S△OCF+S△OEB=S OABC.∵S OABC=10,∴S△OCF+S△OEB=5.∵BE⊥y轴,CF⊥y轴,∴S△OCF==-,S△OEB==3.∴-+3=5.∴k=-4.
17.解:(1)反比例函数y=.列表:
x … -4 -2 -1 1 2 4 …
y … -1 -2 -4 4 2 1 …
描点、连线,反比例函数的图象如图,
(2)由图象可知,当y≥-1时,自变量x的取值范围是x≤-4或x>0.
18.解:(1)设y与x的函数解析式为y=,
∵点(120,0.5)在反比例函数图象上,
∴k=120×0.5=60.
∴y与x的函数解析式为y=.
(2)当y≤3 000=0.3万元时,
即≤0.3,解得x≥200.
答:计划每月偿还贷款不超过3 000元,则至少需要200个月还清.
19.解:(1)∵点B(4,1)在反比例函数图象上,
∴k=4,
∴反比例函数的解析式为y=.
(2)∵点B(4,1),∴点C(-4,-1).
∵点A(a,b)在反比例函数图象上,且4a=b,
∴4a=.∴a=1,b=4,∴点A(1,4).
∴AC==5,
AB==3,
BC==2.
∵AB2+AC2=BC2,
∴AB⊥AC.
∴S△ABC=×5×3=15.
20.解:(1)设y=,
把x=6,y=2代入y=中,得2=,
解得k=12.
∴y关于x的函数解析式为y=.
(2)把x=4代入y=中,得y==3.
∴火焰的像高为3 cm.
(3)由(2)可得,当火焰的像高为3 cm,小孔到蜡烛的距离为4 cm,
∵当x>0时,y随x的增大而减小,
∴若火焰的像高不得超过3 cm,则小孔到蜡烛的距离至少是4 cm.
21.解:(1)∵点A的坐标为(4,3),
∴OA==5.
∵四边形OABC是菱形,
∴AB∥OC,AB=OC=OA=5.
∴点B(4,8),C(0,5).
∵反比例函数y=(k≠0)的图象经过点B,
∴k=4×8=32.
设直线AC的解析式为y=ax+b,
把点A,C的坐标代入,
得解得
∴直线AC的解析式为y=-x+5.
(2)设平移后的直线AC的解析式为
y=-x+5+m,
由
得x2-(10+2m)x+64=0,
当直线AC与反比例函数y=(k≠0)的图象只有一个交点时,
Δ=0,即[-(10+2m)]2-4×1×64=0,
解得m1=3,m2=-13.
故m的值为3或-13.
22.解:(1)∵反比例函数y1=和一次函数y2=mx+n的图象相交于A(-3,a),Ba+,-2两点,
∴k=-3a=-2.
∴a=3.
∴点A(-3,3),B.
∴k=-3×3=-9,
∴y1=-.
把点A(-3,3),B代入
y2=mx+n,
得解得
∴y2=-x+1.
(2)由题图可知,当y1>y2时,自变量x的取值范围为-3.
(3)如图,设AB与y轴相交于点C,
∴点C(0,1),
∴S△AOB=S△BOC+S△AOC
=OC(xB-xA)
=×1×
=.
23.解:(1)24
(2)当0≤x<10时,设AB的解析式为y=kx+b,将点A(0,24),B(10,48)代入,得
解得
∴y=x+24.
(3)张老师能经过适当安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36.理由如下:
在y=x+24中,
当y≥36时,x+24≥36,
解得x≥5.
当20≤x≤40时,反比例函数的解析式为
y=,
当y≥36时,≥36,解得x≤.
∴当5≤x≤时,注意力指标数都不低于36.
而-5=>20,
∴张老师能经过适当安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36.
24.解:(1)把点A(-1,a)代入y=中,得a==2,
∴点A(-1,2).
把点B(m,-1)代入y=中,
得-1=,解得m=2.
∴点B(2,-1).
把点A(-1,2),B(2,-1)代入
y=kx+b(k≠0)中,
得
∴一次函数的解析式为y=-x+1.
(2)由题图可知,不等式(3)-3或5
(满分:120分 时间:120分钟)
一、选择题(共12题,每题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知压力F(N)、压强p(Pa)与受力面积S(m2)之间有如下关系式:F=pS.当F为定值时,如图中大致表示压强p与受力面积S之间函数关系的图象是 ( )
A. B.
C. D.
2.(2024重庆B卷中考)反比例函数y=-的图象一定经过的点是 ( )
A.(1,10) B.(-2,5) C.(2,5) D.(2,8)
3.已知反比例函数y=(k≠0)与一次函数y=2-x的图象的一个交点的横坐标为3,则k的值为 ( )
A.-3 B.-1 C.1 D.3
4.(2024济宁中考)已知点A(-2,y1),B(-1,y2),C(3,y3)在反比例函数y=(k<0)的图象上,则y1,y2,y3的大小关系是( )
A.y1
A. B.
C. D.
6.关于反比例函数y=,下列说法中错误的是 ( )
A.图象必经过点(1,3) B.它的图象分布在第一、第三象限
C.当x>0时,y随x的增大而减小 D.当x>-1时,y<-3
7.如图,四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数y=(k>0)的图象经过第一象限点A,且平行四边形ABCD的面积为4,则k的值是 ( )
A.4 B.-4 C.2 D.-2
8.(2024河北中考)节能环保已成为人们的共识.淇淇家计划购买500度电,若平均每天用电x度,则能使用y天.下列说法错误的是 ( )
A.若x=5,则y=100
B.若y=125,则x=4
C.若x减小,则y也减小
D.若x减小一半,则y增大一倍
9.如图,点A,B是反比例函数y=图象上任意两点,且BD⊥x轴于点D,AC⊥y轴于点C,△OAC和△OBD的面积之和为6,则k的值为 ( )
A.-6 B.-12 C.6 D.12
10.如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在y轴的负半轴上,=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y=,则图象经过点D的反比例函数的解析式是 ( )
A.y=- B.y=-
C.y=- D.y=-
11.如图1所示为某新款茶吧机,开机加热时每分钟上升20 ℃,加热到100 ℃,停止加热,水温开始下降,此时水温y(℃)与通电时间x(min)成反比例函数关系.当水温降至20 ℃时,饮水机再自动加热,若水温在20 ℃时接通电源,水温y(℃)与通电时间x(min)之间的关系如图2所示,则下列说法中错误的是 ( )
图1 图2
A.水温从20 ℃加热到100 ℃,需要4 min
B.水温下降过程中,y与x的函数解析式是y=
C.上午10:00接通电源,可以保证当天10:30能喝到不低于38 ℃的水
D.在一个加热周期内水温不低于40 ℃的时间为7 min
12.(2024长沙模拟)如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一个分支上,分别过点A,C作x轴的垂线段,垂足分别为M和N,给出如下四个结论:①;②阴影部分的面积是(k1+k2);③当∠AOC= 90°时,|k1|=|k2|;④若OABC是菱形,则k1+k2=0.其中正确的是 ( )
A.①③ B.①②③
C.②③④ D.①④
二、填空题(共4题,每题3分,共12分)
13.某反比例函数y=具有下列性质:当x>0时,y随x的增大而减小.写出一个满足条件的k的值是 .
14.(2024山西中考)如图所示的机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数.已知一款机器狗载重后总质量m=60 kg时,它的最快移动速度v=6 m/s;当其载重后总质量m=90 kg时,它的最快移动速度v= m/s.
15.为预防传染病,某校定期对教室进行“药熏消毒”.如图所示,药物燃烧阶段,教室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比例;燃烧后,y与x成反比例.若y>1.6,则x的取值范围是 .
16.如图, ABCO的顶点B在双曲线y=上,顶点C在双曲线y=上,BC的中点P恰好落在y轴上.已知S OABC=10,则k= .
三、解答题(共8题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)已知反比例函数y=.
(1)画出反比例函数的图象.
(2)观察图象,直接写出当y≥-1时,x的取值范围.
18.(6分)(2024吉林二模)小明家购买一套商品房,首付45万元,剩余部分需贷款并按“等额本息”的形式偿还,即贷款金额按月分期还款,且每月偿还贷款金额数相同.若设每月偿还贷款金额y万元,x个月还清,且y是x的反比例函数,其图象如图所示.
(1)求y与x的函数解析式.
(2)若小明家计划每月偿还贷款金额不超过3 000元,则至少需要多少个月还清
19.(6分)如图,点A(a,b),B(4,1)在反比例函数y=的图象上,过点O,B的直线交双曲线的另一支于点C.
(1)求反比例函数的解析式.
(2)连接AC,AB,若4a=b,求△ABC的面积.
20.(10分)大约在两千四五百年前,如图1,墨子和他的学生做了世界上第1个小孔成像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端.”如图2,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
(1)求y关于x的函数解析式.
(2)若小孔到蜡烛的距离为4 cm,求火焰的像高.
(3)若火焰的像高不得超过3 cm,则小孔到蜡烛的距离至少是多少厘米
图1 图2
21.(10分)如图,菱形OABC的顶点O为原点,点C在y轴上,点A的坐标为(4,3),反比例函数y=(k≠0)的图象经过点B.
(1)求k的值和直线AC的解析式.
(2)将直线AC沿y轴平移m个单位长度,当直线AC与反比例函数y=(k≠0)的图象只有一个交点时,求m的值.
22.(10分)(2024广元中考)如图,已知反比例函数y1=和一次函数y2=mx+n的图象相交于A(-3,a), B两点,O为坐标原点,连接OA,OB.
(1)求y1=与y2=mx+n的解析式.
(2)当y1>y2时,请结合图象直接写出自变量x的取值范围.
(3)求△AOB的面积.
23.(12分)(2024天津河东区一模)通过实验研究发现:初中生在数学课上听课注意力指标数随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标数y随时间x(min)变化的函数图象如图所示.当0≤x<10和10≤x<20时,图象是线段;当20≤x≤40时,图象是双曲线的一部分.根据函数图象回答下列问题:
(1)点A的注意力指标数是 .
(2)当0≤x<10时,求注意力指标数y关于时间x(min)的函数解析式.
(3)张老师在一节课上讲解一道数学综合题需要20 min,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36 请说明理由.
24.(12分)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=的图象交于点A(-1,a)与点B(m,-1).
(1)求这个一次函数的解析式.
(2)根据图象,直接写出不等式
【详解答案】
1.D 解析:∵压力F(N)、压强p(Pa)与受力面积S(m2)之间有如下关系式:F=pS.∴当F为定值时,压强p与受力面积S之间的函数关系是反比例函数.故选D.
2.B 解析:当x=1时,y=-10,∴图象不经过点(1,10).故A选项错误;当x=-2时,y=5,∴图象经过点(-2,5).故B选项正确;当x=2时,y=-5,∴图象不经过点(2,5),(2,8).故C选项、D选项错误.故选B.
3.A 解析:将x=3代入y=2-x中,得y=-1.将点(3,-1)代入y=中,得k=-3.故选A.
4.C 解析:在反比例函数y=中k<0,反比例函数图象分布在第二、第四象限,在每个象限内,y随x的增大而增大,∵点C(3,y3)在第四象限,∴y3<0.∵-2<-1,∴0
6.D 解析:∵反比例函数为y=,∴当x=1时,y=3.故A正确,不合题意.∵k=3>0,∴函数图象分布在第一、第三象限.故B正确,不合题意;当x>0时,y随x的增大而减小,故C正确,不合题意.∵x<0时,y随x的增大而减小,且当x=-1时,y=-3,∴当-1
8.C 解析:由题意,得y=.A.若x=5,则y==100,正确,故此选项不符合题意;B.若y=125,则125=,解得x=4.正确,故此选项不符合题意;C.若x减小,则y增大,原说法错误,故此选项符合题意;D.若x减小一半,即y'=,∴y增大一倍.正确,故此选项不符合题意.故选C.
9.A 解析:∵点A,B是反比例函数图象上任意两点,∴设点A,B,∵BD⊥x轴于点D,AC⊥y轴于点C,∴BD=,OD=-b,OC=,AC=-a.∵△OAC和△OBD的面积之和为6,∴×OC·AC+BD·OD=··(-a)+··(-b)=-k-k=-k=6.∴k=-6.故选A.
10.B 解析:如图,过点C作CT⊥y轴于点T,过点D作DH⊥CT交CT的延长线于点H.∵=3,∴设OB=a,则OA=3a.∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠AOB=∠BTC=90°.∴∠ABO+∠CBT=90°,∠CBT+∠BCT=90°.∴∠ABO=∠BCT.∴△AOB≌△BTC(AAS).∴BT=AO=3a,TC=OB=a.∴OT=BT-OB=2a.∴点C(a,2a).∵点C在y=的图象上,∴2a2=1.同理可证△CHD≌△BTC.∴DH=CT=a,CH=BT=3a.∴点D(-2a,3a).设经过点D的反比例函数的解析式为y=,则有-2a×3a=k.∴k=-6a2=-3.∴经过点D的反比例函数的解析式是y=-.故选B.
11.D 解析:∵开机加热时每分钟上升20 ℃,∴水温从20 ℃加热到100 ℃,所需时间为=4(min).故A选项正确,不符合题意;设水温下降过程中,y与x的函数解析式为y=,由题意,得点(4,100)在反比例函数y=的图象上,∴100=.解得k=400.∴水温下降过程中,y与x的函数解析式是y=.故B选项正确,不符合题意;令y=20,则=20,∴x=20.∴从开机加热到水温降至20 ℃需要20 min,即一个循环为20 min,水温y(℃)与通电时间x(min)的函数解析式为
上午10:00到10:30共30 min,30-20=10(min),∴当x=10时,y==40,即此时的水温为40 ℃>38 ℃.故C选项正确,不符合题意;在加热过程中,水温为40 ℃时,20x+20=40,解得x=1.在降温过程中,水温为40 ℃时,40=,解得x=10.∵10-1=9(min),∴一个加热周期内水温不低于40 ℃的时间为9 min.故D选项错误,符合题意.故选D.
12.D 解析:如图,过点A作AE⊥y轴于点E,过点C作CF⊥y轴于点F.∵四边形OABC是平行四边形,∴S△AOB=S△COB.∵OB=OB,∴AE=CF.∴OM=ON.∵S△AOM=|k1|=OM·AM,S△CON=|k2|=ON·CN.∴.故①正确;∵S△AOM=|k1|,S△CON=|k2|,∴S阴影部分=S△AOM+S△CON=(|k1|+|k2|).而k1>0,k2<0,∴S阴影部分=(k1-k2).故②错误;当∠AOC=90°时,四边形OABC是矩形,∴不能确定OA与OC相等.而OM=ON,∴不能判断△AOM≌△CNO.∴不能判断AM=CN.∴不能确定|k1|=|k2|.故③错误;若四边形OABC是菱形,则OA=OC,而OM=ON,∴Rt△AOM≌Rt△CNO(HL).∴AM=CN.∴|k1|=|k2|.∴k1=-k2.∴k1+k2=0.故④正确.故选D.
13.1(答案不唯一) 解析:由题可知,反比例函数y=具有下列性质:当x>0时,y随x的增大而减小,∴k>0.则k的值可以取1.
14.4 解析:设反比例函数解析式为v=,∵机器狗载重后总质量m=60 kg时,它的最快移动速度v=6 m/s,∴k=60×6=360.∴反比例函数解析式为v=.当m=90 kg时,v==4(m/s),故当其载重后总质量m=90 kg时,它的最快移动速度v=4 m/s.
15.2
17.解:(1)反比例函数y=.列表:
x … -4 -2 -1 1 2 4 …
y … -1 -2 -4 4 2 1 …
描点、连线,反比例函数的图象如图,
(2)由图象可知,当y≥-1时,自变量x的取值范围是x≤-4或x>0.
18.解:(1)设y与x的函数解析式为y=,
∵点(120,0.5)在反比例函数图象上,
∴k=120×0.5=60.
∴y与x的函数解析式为y=.
(2)当y≤3 000=0.3万元时,
即≤0.3,解得x≥200.
答:计划每月偿还贷款不超过3 000元,则至少需要200个月还清.
19.解:(1)∵点B(4,1)在反比例函数图象上,
∴k=4,
∴反比例函数的解析式为y=.
(2)∵点B(4,1),∴点C(-4,-1).
∵点A(a,b)在反比例函数图象上,且4a=b,
∴4a=.∴a=1,b=4,∴点A(1,4).
∴AC==5,
AB==3,
BC==2.
∵AB2+AC2=BC2,
∴AB⊥AC.
∴S△ABC=×5×3=15.
20.解:(1)设y=,
把x=6,y=2代入y=中,得2=,
解得k=12.
∴y关于x的函数解析式为y=.
(2)把x=4代入y=中,得y==3.
∴火焰的像高为3 cm.
(3)由(2)可得,当火焰的像高为3 cm,小孔到蜡烛的距离为4 cm,
∵当x>0时,y随x的增大而减小,
∴若火焰的像高不得超过3 cm,则小孔到蜡烛的距离至少是4 cm.
21.解:(1)∵点A的坐标为(4,3),
∴OA==5.
∵四边形OABC是菱形,
∴AB∥OC,AB=OC=OA=5.
∴点B(4,8),C(0,5).
∵反比例函数y=(k≠0)的图象经过点B,
∴k=4×8=32.
设直线AC的解析式为y=ax+b,
把点A,C的坐标代入,
得解得
∴直线AC的解析式为y=-x+5.
(2)设平移后的直线AC的解析式为
y=-x+5+m,
由
得x2-(10+2m)x+64=0,
当直线AC与反比例函数y=(k≠0)的图象只有一个交点时,
Δ=0,即[-(10+2m)]2-4×1×64=0,
解得m1=3,m2=-13.
故m的值为3或-13.
22.解:(1)∵反比例函数y1=和一次函数y2=mx+n的图象相交于A(-3,a),Ba+,-2两点,
∴k=-3a=-2.
∴a=3.
∴点A(-3,3),B.
∴k=-3×3=-9,
∴y1=-.
把点A(-3,3),B代入
y2=mx+n,
得解得
∴y2=-x+1.
(2)由题图可知,当y1>y2时,自变量x的取值范围为-3
(3)如图,设AB与y轴相交于点C,
∴点C(0,1),
∴S△AOB=S△BOC+S△AOC
=OC(xB-xA)
=×1×
=.
23.解:(1)24
(2)当0≤x<10时,设AB的解析式为y=kx+b,将点A(0,24),B(10,48)代入,得
解得
∴y=x+24.
(3)张老师能经过适当安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36.理由如下:
在y=x+24中,
当y≥36时,x+24≥36,
解得x≥5.
当20≤x≤40时,反比例函数的解析式为
y=,
当y≥36时,≥36,解得x≤.
∴当5≤x≤时,注意力指标数都不低于36.
而-5=>20,
∴张老师能经过适当安排,使学生在听这道综合题的讲解时,注意力指标数都不低于36.
24.解:(1)把点A(-1,a)代入y=中,得a==2,
∴点A(-1,2).
把点B(m,-1)代入y=中,
得-1=,解得m=2.
∴点B(2,-1).
把点A(-1,2),B(2,-1)代入
y=kx+b(k≠0)中,
得
∴一次函数的解析式为y=-x+1.
(2)由题图可知,不等式
