期中评估测试卷(含答案) 2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 期中评估测试卷(含答案) 2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 332.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 00:00:00 | ||
图片预览



文档简介
期中评估测试卷
(满分:120分 时间:120分钟)
一、选择题(共12题,每题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如果,那么= ( )
A. B.
C. D.
2.(2024广西中考)已知点M(x1,y1),N(x2,y2)在反比例函数y=的图象上,若x1<0A.y1<0C.y13.下列两个图形一定是相似图形的是 ( )
A.菱形 B.矩形
C.等腰三角形 D.等边三角形
4.在平面直角坐标系中,已知点A(1,0),B(2,1),C(-1,2),以原点O为位似中心,相似比为2,把四边形OABC放大,则点C的对应点C'的坐标为 ( )
A. B.(-2,4)
C.或 D.(-2,4)或(2,-4)
5.如图,已知AD∥BE∥CF,若AB=2BC,DF=12,则EF的长为 ( )
A.2 B.4
C.6 D.8
6.如图,点D,E分别是边AB,AC的中点,点F在DB上,DF=2BF.连接EF并延长,与CB的延长线相交于点M.若BM=2,则线段BC的长为 ( )
A.4 B.6 C.8 D.10
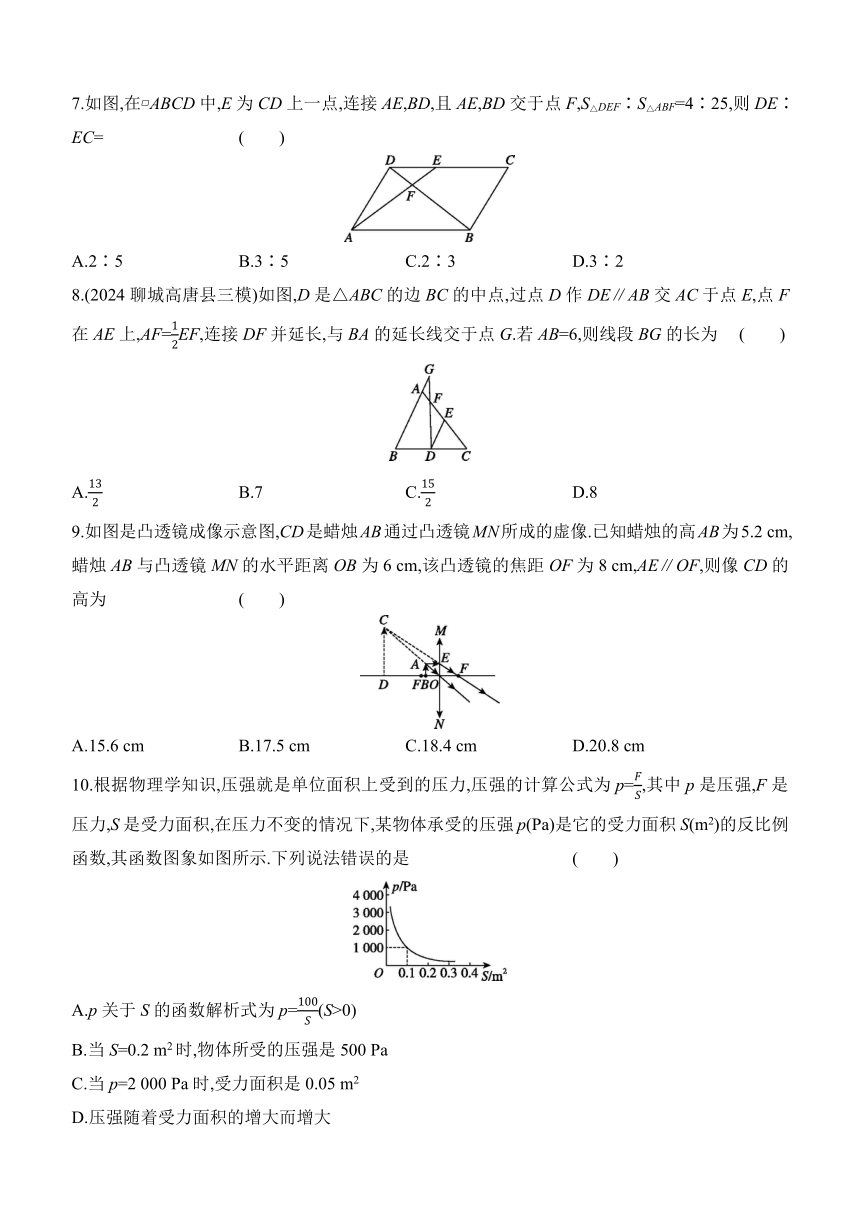
7.如图,在 ABCD中,E为CD上一点,连接AE,BD,且AE,BD交于点F,S△DEF∶S△ABF=4∶25,则DE∶EC= ( )
A.2∶5 B.3∶5 C.2∶3 D.3∶2
8.(2024聊城高唐县三模)如图,D是△ABC的边BC的中点,过点D作DE∥AB交AC于点E,点F在AE上,AF=EF,连接DF并延长,与BA的延长线交于点G.若AB=6,则线段BG的长为 ( )
A. B.7 C. D.8
9.如图是凸透镜成像示意图,CD是蜡烛AB通过凸透镜MN所成的虚像.已知蜡烛的高AB为5.2 cm,蜡烛AB与凸透镜MN的水平距离OB为6 cm,该凸透镜的焦距OF为8 cm,AE∥OF,则像CD的高为 ( )
A.15.6 cm B.17.5 cm C.18.4 cm D.20.8 cm
10.根据物理学知识,压强就是单位面积上受到的压力,压强的计算公式为p=,其中p是压强,F是压力,S是受力面积,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图象如图所示.下列说法错误的是 ( )
A.p关于S的函数解析式为p=(S>0)
B.当S=0.2 m2时,物体所受的压强是500 Pa
C.当p=2 000 Pa时,受力面积是0.05 m2
D.压强随着受力面积的增大而增大
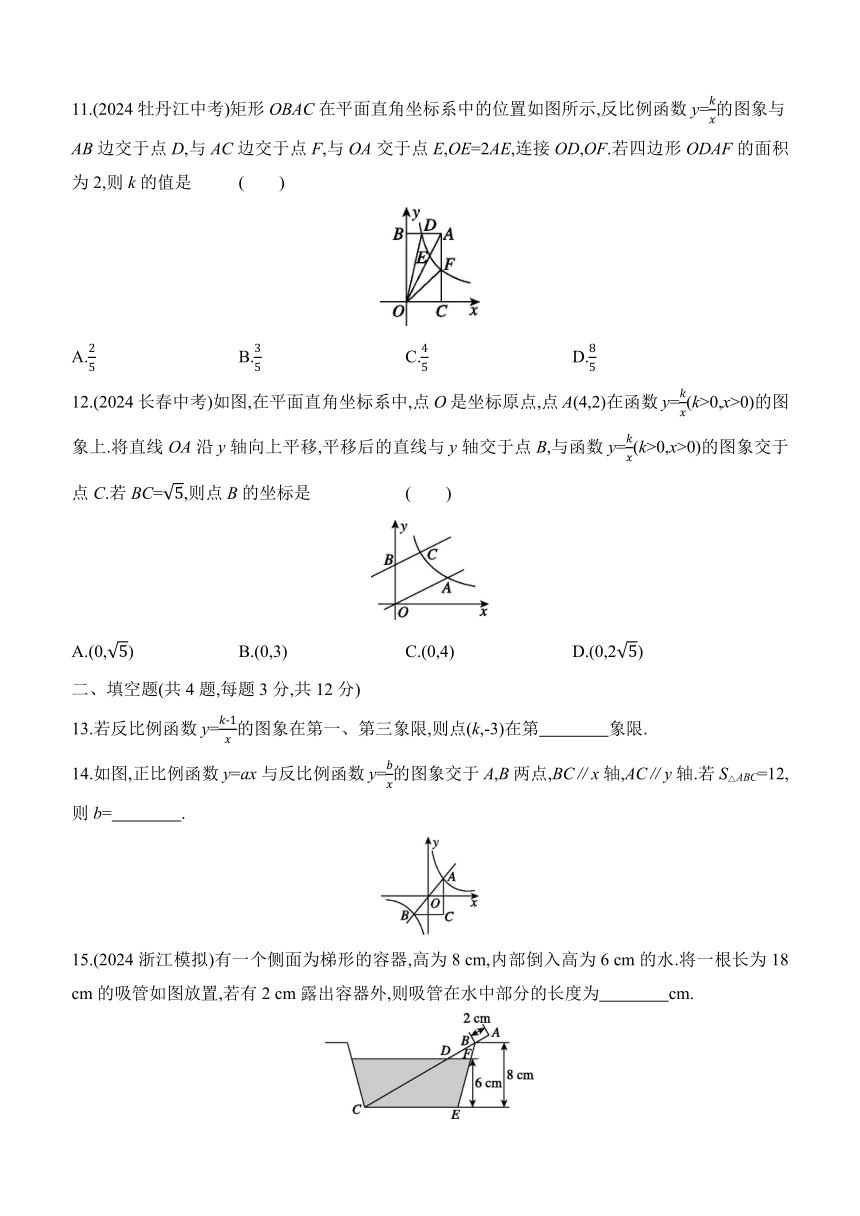
11.(2024牡丹江中考)矩形OBAC在平面直角坐标系中的位置如图所示,反比例函数y=的图象与AB边交于点D,与AC边交于点F,与OA交于点E,OE=2AE,连接OD,OF.若四边形ODAF的面积为2,则k的值是 ( )
A. B. C. D.
12.(2024长春中考)如图,在平面直角坐标系中,点O是坐标原点,点A(4,2)在函数y=(k>0,x>0)的图象上.将直线OA沿y轴向上平移,平移后的直线与y轴交于点B,与函数y=(k>0,x>0)的图象交于点C.若BC=,则点B的坐标是 ( )
A.(0,) B.(0,3) C.(0,4) D.(0,2)
二、填空题(共4题,每题3分,共12分)
13.若反比例函数y=的图象在第一、第三象限,则点(k,-3)在第 象限.
14.如图,正比例函数y=ax与反比例函数y=的图象交于A,B两点,BC∥x轴,AC∥y轴.若S△ABC=12,则b= .
15.(2024浙江模拟)有一个侧面为梯形的容器,高为8 cm,内部倒入高为6 cm的水.将一根长为18 cm的吸管如图放置,若有2 cm露出容器外,则吸管在水中部分的长度为 cm.
16.(2024眉山中考)如图,菱形ABCD的边长为6,∠BAD=120°,过点D作DE⊥BC,交BC的延长线于点E,连接AE分别交BD,CD于点F,G,则FG的长为 .
三、解答题(共8题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(3,-1),B(3,3),C(1,-2).
(1)画出△ABC以点O为位似中心的位似图形△A1B1C1,使得△ABC与△A1B1C1的相似比为1∶2,且点B1落在第三象限.
(2)直接写出△A1B1C1各顶点的坐标.
(3)直接写出△A1B1C1的面积.
18.(8分)(2024青海中考)如图,在同一平面直角坐标系中,一次函数y=-x+b和反比例函数y=的图象交于点A(1,m),B(n,1).
(1)求点A,B的坐标及一次函数的解析式.
(2)根据图象,直接写出不等式-x+b>的解集.
19.(8分)很多学生由于用眼不科学,导致视力下降,需要佩戴眼镜.研究发现,近视眼镜的度数y(度)与镜片焦距x(m)成反比例函数关系,其函数图象如图所示.
(1)当近视眼镜的度数是200度时,镜片焦距是多少米
(2)明明原来佩戴275度的近视眼镜,经过一段时间的矫正治疗并注意用眼健康,复查验光后,所配镜片的焦距调整到了0.4 m,则明明的眼镜度数下降了多少度
20.(8分)(2024盐城中考)如图,点C在以AB为直径的☉O上,过点C作☉O的切线l,过点A作AD⊥l,垂足为D,连接AC,BC.
(1)求证:△ABC∽△ACD.
(2)若AC=5,CD=4,求☉O的半径.
21.(8分)如图,在△ABC中,AB=AC,AD是BC边上的高线,点E,F分别在AC,CD上,且∠1=∠2.
(1)求证:AD∥EF.
(2)当CE∶AE=3∶5,CF=6时,求BC的长.
22.(8分)(2024西安雁塔区模拟)西安鼓楼,位于古都西安市的中心,是全国重点文物保护单位,也是西安的标志性建筑.学校某实践小组根据课堂所学知识,想实地测量西安鼓楼AB的高度.如图,测量小组在点F处直立一个2 m高的标杆EF,随后小组成员沿直线BF移动测量.成员小王从点F后退4 m到达点G处,此时鼓楼顶端A、标杆顶端E、点G恰好在一条直线上;小王从点G继续后退18 m到达点H处.这时,他在点H处的地面上水平放置一个平面镜.成员小李沿BH方向移动到点N处时,小李刚好在平面镜内看到鼓楼顶端A的像.此时测得HN=3.75 m,小李眼睛与地面的距离MN=1.5 m.已知点B,F,G,H,N在同一水平直线上,且AB,EF,MN均垂直于BN.求鼓楼AB的高度.(平面镜的大小忽略不计)
23.(10分)某项研究表明,眼睛的疲劳系数y与睡眠时间t(单位:h)之间成函数关系,它们之间的函数关系图象如图所示.当0(1)试分别求出当0(2)当睡眠时间t=5时,求眼睛的疲劳系数y.
(3)当眼睛的疲劳系数y的范围为2≤y≤2.5时,求睡眠时间t的取值范围.
24.(12分)(2024泰安中考)如图,直线y1=kx+b(k≠0)与反比例函数y2=-的图象相交于点A(-2,m), B(n,-1),与y轴交于点C.
(1)求直线y1的解析式.
(2)若y1>y2,请直接写出满足条件的x的取值范围.
(3)过点C作x轴的平行线交反比例函数的图象于点D,求△ACD的面积.
【详解答案】
1.C 解析:∵,∴.故选C.
2.A 解析:∵2>0,∴反比例函数y=的图象在第一、第三象限.∵x1<03.D 解析:A.两个菱形的对应边的比相等,但对应角不一定相等,不一定是相似图形,故此选项不符合题意;B.两个矩形的对应角相等,但对应边的比不一定相等,不一定是相似图形,故此选项不符合题意;C.两等腰三角形不一定相似,故此选项不符合题意;D.两个等边三角形一定相似,故此选项符合题意.故选D.
4.D 解析:∵点A(1,0),B(2,1),C(-1,2),以原点O为位似中心,相似比为2,把四边形OABC放大,∴点的C对应点C'的坐标为(-2,4)或(2,-4).故选D.
5.B 解析:∵AD∥BE∥CF,∴.
∵AB=2BC,∴=2,即DE=2EF.
∵DF=12,∴DF=DE+EF=2EF+EF=3EF=12.∴EF=4.故选B.
6.C 解析:∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线.∴DE∥BC,且BC=2DE.
∵DE∥BM,DF=2BF,∴,即=2.∴DE=4.∴BC=2DE=2×4=8.故选C.
7.C 解析:∵四边形ABCD是平行四边形,
∴AB∥CD.∴∠FAB=∠FED,∠AFB=∠EFD.∴△BAF∽△DEF.∵S△DEF∶S△ABF=4∶25,∴DE∶AB=2∶5.
∵AB=CD,∴DE∶EC=2∶3.故选C.
8.C 解析:∵D是BC的中点,DE∥AB,∴DE是△ABC的中位线.∴DE=AB=×6=3.
∵DE∥AB,∴△AGF∽△EDF.∴.∵AF=EF,∴.∴AG=ED=.∴BG=AB+AG=6+.故选C.
9.D 解析:由题意,得AB∥MN,AE∥OF,AB∥CD,∴四边形ABOE是平行四边形.∴AE=BO=6 cm.∵AE∥OF,∴△CAE∽△COF.∴.∴.∵AB∥CD,∴△OAB∽△OCD.∴.∴.∴CD=20.8 cm.故选D.
10.D 解析:由题中图象可得,点(0.1,1 000)在函数图象上,∴1 000=.解得F=100.∴p=(S>0).故选项A正确,不符合题意;当S=0.2 m2时,物体所受的压强是=500(Pa),故选项B正确,不符合题意;当p=2 000 Pa时,受力面积是=0.05(m2),故选项C正确,不符合题意;压强随着受力面积的增大而减小,故选项D错误,符合题意.故选D.
11.D 解析:如图,过点E作EM⊥OC于点M,则EM∥OB∥AC,
∴△OME∽△OCA.∴.
设点E,∴OM=a,EM=.
∵OE=2AE,∴.∴OC=a,AC=·.∴S矩形OBAC=S△OBD+S△OCF+S四边形ODAF=a··,即+2=a··.解得k=.故选D.
12.B 解析:∵点A(4,2)在函数y=上,∴k=4×2=8.∴反比例函数的解析式为y=.设直线OA的解析式为y=kx,∴4k=2.∴k=.∴直线OA的解析式为y=x.又设向上平移m个单位长度得到直线BC,∴点B(0,m),直线BC的解析式为y=x+m.再设点Ca,(a>0),∴a+m.∴-m=a.如图,过点C作CH⊥y轴于点H,
∴CH=a,BH=-m=a,BH2+CH2=BC2.∴a2+a2=5.∴a=2.∴4-m=1.∴m=3.∴点B(0,3).故选B.
13.四 解析:∵反比例函数y=的图象在第一、第三象限,∴k-1>0.解得k>1.∴点(k,-3)在第四象限.
14.6 解析:设点A的坐标为m,,则点B的坐标为-m,-.∴点C的坐标为m,-.∴AC=,BC=2m.∴△ABC的面积=AC·BC=·2m·=12.∴b=6.
15.12 解析:如图,过点B作BM⊥CE,垂足为M,过点F作FN⊥CE,垂足为N,
∵DF∥CE,∴∠BDF=∠BCE.∵∠DBF=∠CBE,∴△BDF∽△BCE.∵BM=8 cm,FN=6 cm,BC=18-2=16(cm),∴设CD=x cm,则BD=(16-x)cm.∵△BDF的高为BM-FN=8-6=2(cm),∴.∴.解得x=12.∴CD=12 cm.
16. 解析:∵菱形ABCD的边长为6,∠BAD=120°,∴AD=BC=CD=6,AD∥BC,∠BCD=120°.∴∠DCE=60°.∵DE⊥BC,∴∠DEC=90°.在Rt△DCE中,∵∠CDE=90°-∠DCE=30°,∴CE=CD=3.∴DE==3.∴BE=BC+CE=9.∵AD∥BE,∴∠ADE=180°-∠DEC=90°.在Rt△ADE中,AE==3.∵AD∥BE,∴△AFD∽△EFB.∴.∴AF=AE=×3.∵AD∥CE,∴△AGD∽△EGC.∴=2.∴AG=AE=×3=2.∴FG=AG-AF=2.
17.解:(1)如图,△A1B1C1即为所求.
(2)由图可得,点A1(-6,2),B1(-6,-6),C1(-2,4).
(3)△A1B1C1的面积为16.
18.解:(1)把点A(1,m)代入 y=中,
得m==9.
∴点A的坐标为(1,9),
把点B(n,1)代入 y=中,
得n==9.
∴点B的坐标为(9,1).
把x=1,y=9代入y=-x+b中,
得-1+b=9,∴b=10.
∴一次函数的解析式为y=-x+10.
(2)x<0或119.解:(1)设近视眼镜的度数y(度)与镜片焦距x(m)的反比例函数解析式为y=,
由题图可知,当x=0.25时,y=400,
∴400=.∴k=100.
∴反比例函数的解析式为y=.
当y=200时,x==0.5.
答:当近视眼镜的度数是200度时,镜片焦距是0.5 m.
(2)当x=0.4 m时,y==250(度),
275-250=25(度).
答:明明的眼镜度数下降了25度.
20.解:(1)证明:如图,连接OC,
∵l是☉O的切线,∴OC⊥l.
∵AD⊥l,∴OC∥AD.
∴∠CAD=∠ACO.
∵OA=OC,∴∠OAC=∠OCA.
∴∠CAD=∠BAC.
∵∠ACB=∠ADC=90°,
∴△ABC∽△ACD.
(2)∵AC=5,CD=4,∠ADC=90°,
∴AD==3.
∵△ABC∽△ACD,∴.
∴.∴AB=.
∴☉O的半径为.
21.解:(1)证明:∵AB=AC,AD是BC边上的高线,
∴BD=DC,∠1=∠CAD.
∵∠1=∠2,∴∠CAD=∠2.
∴EF∥AD.
(2)∵EF∥AD,∴.
∵CE∶AE=3∶5,CF=6,
∴.解得FD=10.
∴CD=CF+DF=6+10=16.
∴BC=2CD=32.
22.解:∵AB,EF,MN均垂直于BN,
∴AB∥EF∥MN.∴△EFG∽△ABG.
∵EF=2 m,FG=4 m,
设BF=x m,
∴,即.
∴AB=2+.
由反射角等于入射角,得∠AHB=∠MHN,
∵∠ABH=∠MNH=90°,
∴△AHB∽△MHN.
∴,即.
又∵AB=2+,解得x=68.
∴AB=36 m.
∴鼓楼AB的高度为36 m.
23.解:(1)设当0∵点(4.5,2)在反比例函数图象上,
∴k=4.5×2=9.
∴反比例函数的解析式为y=(0设当4.5≤t≤6时一次函数的解析式为y=mt+n,点(4.5,2),(6,0)在一次函数图象上,
解得
∴一次函数的解析式为y=-t+8(4.5≤t≤6).
(2)将t=5代入一次函数解析式,得
y=-×5+8=.
∴眼睛的疲劳系数y为.
(3)当y=2时,t=4.5,
当y=2.5时,t=3.6,
∴当眼睛的疲劳系数y的范围为2≤y≤2.5时,睡眠时间t的取值范围为3.6≤t≤4.5.
24.解:(1)分别将点A(-2,m)、点B(n,-1)代入y2=-中,
得-2m=-8,-n=-8.
解得m=4,n=8.
∴点A的坐标为(-2,4),点B的坐标为(8,-1).
把点A(-2,4),B(8,-1)分别代入 y1=kx+b,
得解得
∴直线y1的解析式为y1=-x+3.
(2)x<-2或0(3)当x=0时,y1=0+3=3,
∴点C(0,3).
把y=3代入y2=-中,得x=-.
∴点D的坐标为.
∴CD=.
∴S△ACD=×(4-3)=.
(满分:120分 时间:120分钟)
一、选择题(共12题,每题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如果,那么= ( )
A. B.
C. D.
2.(2024广西中考)已知点M(x1,y1),N(x2,y2)在反比例函数y=的图象上,若x1<0
A.菱形 B.矩形
C.等腰三角形 D.等边三角形
4.在平面直角坐标系中,已知点A(1,0),B(2,1),C(-1,2),以原点O为位似中心,相似比为2,把四边形OABC放大,则点C的对应点C'的坐标为 ( )
A. B.(-2,4)
C.或 D.(-2,4)或(2,-4)
5.如图,已知AD∥BE∥CF,若AB=2BC,DF=12,则EF的长为 ( )
A.2 B.4
C.6 D.8
6.如图,点D,E分别是边AB,AC的中点,点F在DB上,DF=2BF.连接EF并延长,与CB的延长线相交于点M.若BM=2,则线段BC的长为 ( )
A.4 B.6 C.8 D.10
7.如图,在 ABCD中,E为CD上一点,连接AE,BD,且AE,BD交于点F,S△DEF∶S△ABF=4∶25,则DE∶EC= ( )
A.2∶5 B.3∶5 C.2∶3 D.3∶2
8.(2024聊城高唐县三模)如图,D是△ABC的边BC的中点,过点D作DE∥AB交AC于点E,点F在AE上,AF=EF,连接DF并延长,与BA的延长线交于点G.若AB=6,则线段BG的长为 ( )
A. B.7 C. D.8
9.如图是凸透镜成像示意图,CD是蜡烛AB通过凸透镜MN所成的虚像.已知蜡烛的高AB为5.2 cm,蜡烛AB与凸透镜MN的水平距离OB为6 cm,该凸透镜的焦距OF为8 cm,AE∥OF,则像CD的高为 ( )
A.15.6 cm B.17.5 cm C.18.4 cm D.20.8 cm
10.根据物理学知识,压强就是单位面积上受到的压力,压强的计算公式为p=,其中p是压强,F是压力,S是受力面积,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图象如图所示.下列说法错误的是 ( )
A.p关于S的函数解析式为p=(S>0)
B.当S=0.2 m2时,物体所受的压强是500 Pa
C.当p=2 000 Pa时,受力面积是0.05 m2
D.压强随着受力面积的增大而增大
11.(2024牡丹江中考)矩形OBAC在平面直角坐标系中的位置如图所示,反比例函数y=的图象与AB边交于点D,与AC边交于点F,与OA交于点E,OE=2AE,连接OD,OF.若四边形ODAF的面积为2,则k的值是 ( )
A. B. C. D.
12.(2024长春中考)如图,在平面直角坐标系中,点O是坐标原点,点A(4,2)在函数y=(k>0,x>0)的图象上.将直线OA沿y轴向上平移,平移后的直线与y轴交于点B,与函数y=(k>0,x>0)的图象交于点C.若BC=,则点B的坐标是 ( )
A.(0,) B.(0,3) C.(0,4) D.(0,2)
二、填空题(共4题,每题3分,共12分)
13.若反比例函数y=的图象在第一、第三象限,则点(k,-3)在第 象限.
14.如图,正比例函数y=ax与反比例函数y=的图象交于A,B两点,BC∥x轴,AC∥y轴.若S△ABC=12,则b= .
15.(2024浙江模拟)有一个侧面为梯形的容器,高为8 cm,内部倒入高为6 cm的水.将一根长为18 cm的吸管如图放置,若有2 cm露出容器外,则吸管在水中部分的长度为 cm.
16.(2024眉山中考)如图,菱形ABCD的边长为6,∠BAD=120°,过点D作DE⊥BC,交BC的延长线于点E,连接AE分别交BD,CD于点F,G,则FG的长为 .
三、解答题(共8题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(3,-1),B(3,3),C(1,-2).
(1)画出△ABC以点O为位似中心的位似图形△A1B1C1,使得△ABC与△A1B1C1的相似比为1∶2,且点B1落在第三象限.
(2)直接写出△A1B1C1各顶点的坐标.
(3)直接写出△A1B1C1的面积.
18.(8分)(2024青海中考)如图,在同一平面直角坐标系中,一次函数y=-x+b和反比例函数y=的图象交于点A(1,m),B(n,1).
(1)求点A,B的坐标及一次函数的解析式.
(2)根据图象,直接写出不等式-x+b>的解集.
19.(8分)很多学生由于用眼不科学,导致视力下降,需要佩戴眼镜.研究发现,近视眼镜的度数y(度)与镜片焦距x(m)成反比例函数关系,其函数图象如图所示.
(1)当近视眼镜的度数是200度时,镜片焦距是多少米
(2)明明原来佩戴275度的近视眼镜,经过一段时间的矫正治疗并注意用眼健康,复查验光后,所配镜片的焦距调整到了0.4 m,则明明的眼镜度数下降了多少度
20.(8分)(2024盐城中考)如图,点C在以AB为直径的☉O上,过点C作☉O的切线l,过点A作AD⊥l,垂足为D,连接AC,BC.
(1)求证:△ABC∽△ACD.
(2)若AC=5,CD=4,求☉O的半径.
21.(8分)如图,在△ABC中,AB=AC,AD是BC边上的高线,点E,F分别在AC,CD上,且∠1=∠2.
(1)求证:AD∥EF.
(2)当CE∶AE=3∶5,CF=6时,求BC的长.
22.(8分)(2024西安雁塔区模拟)西安鼓楼,位于古都西安市的中心,是全国重点文物保护单位,也是西安的标志性建筑.学校某实践小组根据课堂所学知识,想实地测量西安鼓楼AB的高度.如图,测量小组在点F处直立一个2 m高的标杆EF,随后小组成员沿直线BF移动测量.成员小王从点F后退4 m到达点G处,此时鼓楼顶端A、标杆顶端E、点G恰好在一条直线上;小王从点G继续后退18 m到达点H处.这时,他在点H处的地面上水平放置一个平面镜.成员小李沿BH方向移动到点N处时,小李刚好在平面镜内看到鼓楼顶端A的像.此时测得HN=3.75 m,小李眼睛与地面的距离MN=1.5 m.已知点B,F,G,H,N在同一水平直线上,且AB,EF,MN均垂直于BN.求鼓楼AB的高度.(平面镜的大小忽略不计)
23.(10分)某项研究表明,眼睛的疲劳系数y与睡眠时间t(单位:h)之间成函数关系,它们之间的函数关系图象如图所示.当0
(3)当眼睛的疲劳系数y的范围为2≤y≤2.5时,求睡眠时间t的取值范围.
24.(12分)(2024泰安中考)如图,直线y1=kx+b(k≠0)与反比例函数y2=-的图象相交于点A(-2,m), B(n,-1),与y轴交于点C.
(1)求直线y1的解析式.
(2)若y1>y2,请直接写出满足条件的x的取值范围.
(3)过点C作x轴的平行线交反比例函数的图象于点D,求△ACD的面积.
【详解答案】
1.C 解析:∵,∴.故选C.
2.A 解析:∵2>0,∴反比例函数y=的图象在第一、第三象限.∵x1<0
4.D 解析:∵点A(1,0),B(2,1),C(-1,2),以原点O为位似中心,相似比为2,把四边形OABC放大,∴点的C对应点C'的坐标为(-2,4)或(2,-4).故选D.
5.B 解析:∵AD∥BE∥CF,∴.
∵AB=2BC,∴=2,即DE=2EF.
∵DF=12,∴DF=DE+EF=2EF+EF=3EF=12.∴EF=4.故选B.
6.C 解析:∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线.∴DE∥BC,且BC=2DE.
∵DE∥BM,DF=2BF,∴,即=2.∴DE=4.∴BC=2DE=2×4=8.故选C.
7.C 解析:∵四边形ABCD是平行四边形,
∴AB∥CD.∴∠FAB=∠FED,∠AFB=∠EFD.∴△BAF∽△DEF.∵S△DEF∶S△ABF=4∶25,∴DE∶AB=2∶5.
∵AB=CD,∴DE∶EC=2∶3.故选C.
8.C 解析:∵D是BC的中点,DE∥AB,∴DE是△ABC的中位线.∴DE=AB=×6=3.
∵DE∥AB,∴△AGF∽△EDF.∴.∵AF=EF,∴.∴AG=ED=.∴BG=AB+AG=6+.故选C.
9.D 解析:由题意,得AB∥MN,AE∥OF,AB∥CD,∴四边形ABOE是平行四边形.∴AE=BO=6 cm.∵AE∥OF,∴△CAE∽△COF.∴.∴.∵AB∥CD,∴△OAB∽△OCD.∴.∴.∴CD=20.8 cm.故选D.
10.D 解析:由题中图象可得,点(0.1,1 000)在函数图象上,∴1 000=.解得F=100.∴p=(S>0).故选项A正确,不符合题意;当S=0.2 m2时,物体所受的压强是=500(Pa),故选项B正确,不符合题意;当p=2 000 Pa时,受力面积是=0.05(m2),故选项C正确,不符合题意;压强随着受力面积的增大而减小,故选项D错误,符合题意.故选D.
11.D 解析:如图,过点E作EM⊥OC于点M,则EM∥OB∥AC,
∴△OME∽△OCA.∴.
设点E,∴OM=a,EM=.
∵OE=2AE,∴.∴OC=a,AC=·.∴S矩形OBAC=S△OBD+S△OCF+S四边形ODAF=a··,即+2=a··.解得k=.故选D.
12.B 解析:∵点A(4,2)在函数y=上,∴k=4×2=8.∴反比例函数的解析式为y=.设直线OA的解析式为y=kx,∴4k=2.∴k=.∴直线OA的解析式为y=x.又设向上平移m个单位长度得到直线BC,∴点B(0,m),直线BC的解析式为y=x+m.再设点Ca,(a>0),∴a+m.∴-m=a.如图,过点C作CH⊥y轴于点H,
∴CH=a,BH=-m=a,BH2+CH2=BC2.∴a2+a2=5.∴a=2.∴4-m=1.∴m=3.∴点B(0,3).故选B.
13.四 解析:∵反比例函数y=的图象在第一、第三象限,∴k-1>0.解得k>1.∴点(k,-3)在第四象限.
14.6 解析:设点A的坐标为m,,则点B的坐标为-m,-.∴点C的坐标为m,-.∴AC=,BC=2m.∴△ABC的面积=AC·BC=·2m·=12.∴b=6.
15.12 解析:如图,过点B作BM⊥CE,垂足为M,过点F作FN⊥CE,垂足为N,
∵DF∥CE,∴∠BDF=∠BCE.∵∠DBF=∠CBE,∴△BDF∽△BCE.∵BM=8 cm,FN=6 cm,BC=18-2=16(cm),∴设CD=x cm,则BD=(16-x)cm.∵△BDF的高为BM-FN=8-6=2(cm),∴.∴.解得x=12.∴CD=12 cm.
16. 解析:∵菱形ABCD的边长为6,∠BAD=120°,∴AD=BC=CD=6,AD∥BC,∠BCD=120°.∴∠DCE=60°.∵DE⊥BC,∴∠DEC=90°.在Rt△DCE中,∵∠CDE=90°-∠DCE=30°,∴CE=CD=3.∴DE==3.∴BE=BC+CE=9.∵AD∥BE,∴∠ADE=180°-∠DEC=90°.在Rt△ADE中,AE==3.∵AD∥BE,∴△AFD∽△EFB.∴.∴AF=AE=×3.∵AD∥CE,∴△AGD∽△EGC.∴=2.∴AG=AE=×3=2.∴FG=AG-AF=2.
17.解:(1)如图,△A1B1C1即为所求.
(2)由图可得,点A1(-6,2),B1(-6,-6),C1(-2,4).
(3)△A1B1C1的面积为16.
18.解:(1)把点A(1,m)代入 y=中,
得m==9.
∴点A的坐标为(1,9),
把点B(n,1)代入 y=中,
得n==9.
∴点B的坐标为(9,1).
把x=1,y=9代入y=-x+b中,
得-1+b=9,∴b=10.
∴一次函数的解析式为y=-x+10.
(2)x<0或1
由题图可知,当x=0.25时,y=400,
∴400=.∴k=100.
∴反比例函数的解析式为y=.
当y=200时,x==0.5.
答:当近视眼镜的度数是200度时,镜片焦距是0.5 m.
(2)当x=0.4 m时,y==250(度),
275-250=25(度).
答:明明的眼镜度数下降了25度.
20.解:(1)证明:如图,连接OC,
∵l是☉O的切线,∴OC⊥l.
∵AD⊥l,∴OC∥AD.
∴∠CAD=∠ACO.
∵OA=OC,∴∠OAC=∠OCA.
∴∠CAD=∠BAC.
∵∠ACB=∠ADC=90°,
∴△ABC∽△ACD.
(2)∵AC=5,CD=4,∠ADC=90°,
∴AD==3.
∵△ABC∽△ACD,∴.
∴.∴AB=.
∴☉O的半径为.
21.解:(1)证明:∵AB=AC,AD是BC边上的高线,
∴BD=DC,∠1=∠CAD.
∵∠1=∠2,∴∠CAD=∠2.
∴EF∥AD.
(2)∵EF∥AD,∴.
∵CE∶AE=3∶5,CF=6,
∴.解得FD=10.
∴CD=CF+DF=6+10=16.
∴BC=2CD=32.
22.解:∵AB,EF,MN均垂直于BN,
∴AB∥EF∥MN.∴△EFG∽△ABG.
∵EF=2 m,FG=4 m,
设BF=x m,
∴,即.
∴AB=2+.
由反射角等于入射角,得∠AHB=∠MHN,
∵∠ABH=∠MNH=90°,
∴△AHB∽△MHN.
∴,即.
又∵AB=2+,解得x=68.
∴AB=36 m.
∴鼓楼AB的高度为36 m.
23.解:(1)设当0
∴k=4.5×2=9.
∴反比例函数的解析式为y=(0
解得
∴一次函数的解析式为y=-t+8(4.5≤t≤6).
(2)将t=5代入一次函数解析式,得
y=-×5+8=.
∴眼睛的疲劳系数y为.
(3)当y=2时,t=4.5,
当y=2.5时,t=3.6,
∴当眼睛的疲劳系数y的范围为2≤y≤2.5时,睡眠时间t的取值范围为3.6≤t≤4.5.
24.解:(1)分别将点A(-2,m)、点B(n,-1)代入y2=-中,
得-2m=-8,-n=-8.
解得m=4,n=8.
∴点A的坐标为(-2,4),点B的坐标为(8,-1).
把点A(-2,4),B(8,-1)分别代入 y1=kx+b,
得解得
∴直线y1的解析式为y1=-x+3.
(2)x<-2或0
∴点C(0,3).
把y=3代入y2=-中,得x=-.
∴点D的坐标为.
∴CD=.
∴S△ACD=×(4-3)=.
同课章节目录
