1.2从立体图形到平面图形 课件(共45张PPT)
文档属性
| 名称 | 1.2从立体图形到平面图形 课件(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 12:16:31 | ||
图片预览







文档简介
(共45张PPT)
第一单元 丰富的图形世界
第二节 从立体图形到平面图形
(2024鲁教版)六年级上
学习目标
观察立体图形
01
02
展开立体图形
03
综合提升
一、观察立体图形
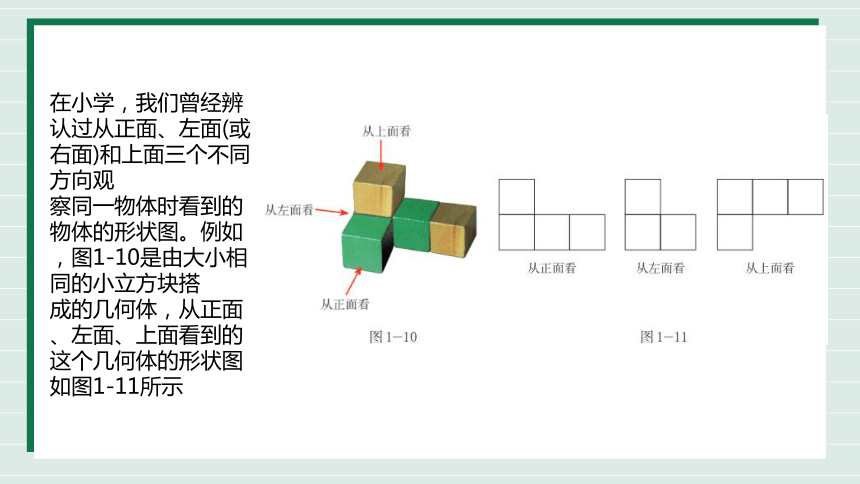
在小学,我们曾经辨认过从正面、左面(或右面)和上面三个不同方向观
察同一物体时看到的物体的形状图。例如,图1-10是由大小相同的小立方块搭
成的几何体,从正面、左面、上面看到的这个几何体的形状图如图1-11所示
请你用6个大小相同的小立方块搭一个几何体,然后请同伴画出从正面
左面、上面看到的这个几何体的形状图。
一个几何体由多个大小相同的小立方块搭成,从上面和从左面看到的这
个几何体的形状图如图1-12所示,请搭出满足条件的几何体。你搭的几何体
由几个小立方块构成
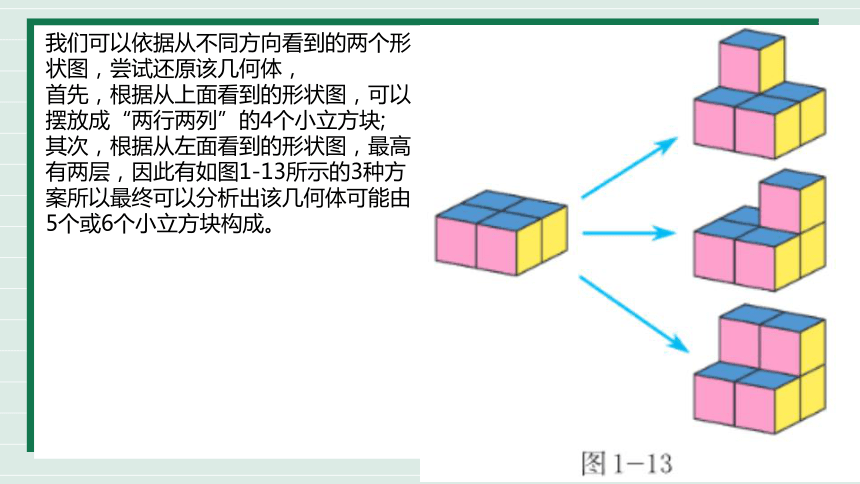
我们可以依据从不同方向看到的两个形状图,尝试还原该几何体,
首先,根据从上面看到的形状图,可以摆放成“两行两列”的4个小立方块;
其次,根据从左面看到的形状图,最高有两层,因此有如图1-13所示的3种方案所以最终可以分析出该几何体可能由5个或6个小立方块构成。
(1)请你选择若干如图1-14所示的立方块和长
方块搭一个几何体,然后请同伴画出从正面、左面、
上面看到的这个几何体的形状图
(2)请你画出从正面、左面、上面看到的一个几何体(由若干如图1-14所示的立方块和长方块搭成)的形状图,然后请同
伴根据你画的形状图搭出相应的几何体。与同伴进行交流。
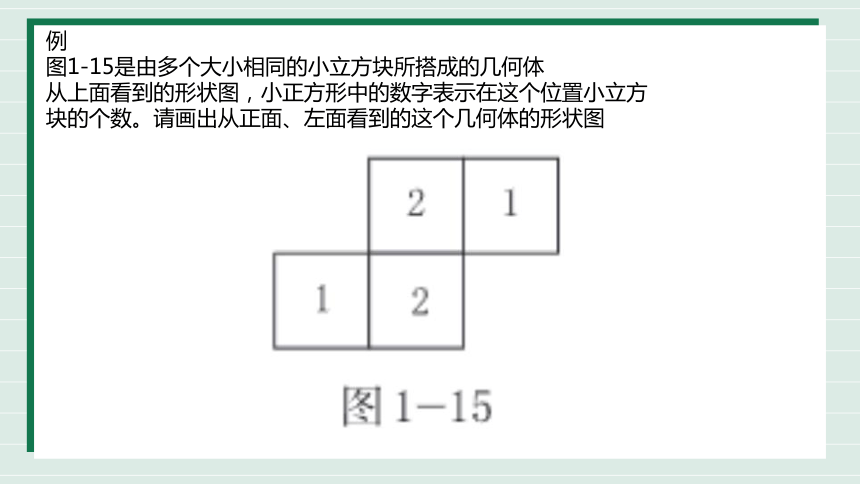
例
图1-15是由多个大小相同的小立方块所搭成的几何体
从上面看到的形状图,小正方形中的数字表示在这个位置小立方
块的个数。请画出从正面、左面看到的这个几何体的形状图
解法一:先用实物摆出这个几何体,再画出从正面、左面看到的它的形
状图(如图 1-16)。
解法二:根据从上面看到的形状图确定从正面看到的形状图有3列,从
左面看到的形状图有2行,再根据小正方形中的数字确定每行每列小立方块的个数。
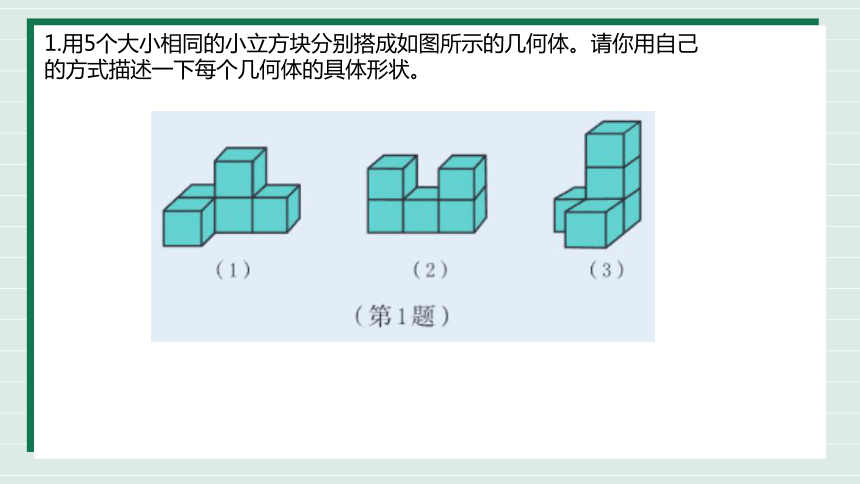
1.用5个大小相同的小立方块分别搭成如图所示的几何体。请你用自己
的方式描述一下每个几何体的具体形状。
2.一个几何体由多个大小相同的小立方块搭成,从上面观察这个几何
体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小
立方块的个数。请画出从正面、左面看到的这个几何体的形状图
二、立体图形展开
还记得小学学过的正方体表面的展开图吗
将如图1-17所示的正方体沿图中红色的棱剪开,请画出它
的展开图
将一个正方体的表面沿某些棱剪开,展开成一个平面图形(展开后每个
面至少有一条边与其他面相连),你能得到哪些形状的展开图
(1)观察正方体的展开图,原正方体中未剪开的棱有几条 剪开的棱有
几条
(2)你能得到图1-18中的展开图吗
图1-19中的图形经过折叠能否围成一个正方体 你是如何判断的 与同
伴进行交流。
图1-20中的图形经过折叠可以围成一个正方体形的盒子。折好以后,与
1”面相邻的面是什么 相对的面是什么 先想一想,再折一折,看看你的
想法是否正确。
1.下面哪个图形经过折叠可以得到正方体
2.将正方体的表面分别标上数字1,2,3,4,5,6,使它的任意两个相对面
上的数字之和为 7。将它沿某些棱剪开,能得到下面的展开图吗
3.在图中增加1个大小相同的小正方形,使所得图形经
过折叠能够围成一个正方体。先想一想,再试一试。
将图1-21中的棱柱沿某些棱剪开,你能得到哪些形状的展开图 与同伴
进行交流。
和正方体一样,我们沿着棱柱的某些棱剪开,就得到了它的展开图。由
于剪开的方式不一样,我们得到的展开图也就不一样。
图1-22是三棱柱的部分展开图。
与同伴交流四棱柱的展开图、五棱柱的展开图,
直棱柱的展开图是由两个相同的多边形(底面)和一些长方形(侧面
按照不同的方式组合而成的。
(1)如图1-23,哪些图形经过折叠可以围成一个棱柱 先想一想,再折一折。
(2)适当修改图1-23中不能围成棱柱的图形,使所得图形能围成一个棱柱。
一个长方体的长、宽、高分别为5cm,4cm,3cm,请画出它的展开图
并与同伴进行交流。
(1)按照图1-24所示的方法把无底面的圆柱、圆锥的侧面展开,会得
到什么图形 先想一想,再做一做。
2)你的想法是否正确
如图1-25,圆柱的侧面展开图是长方形,圆锥的侧面展开图是扇形
在展开与折叠的活动中,你积累了哪些经验
1.下列图形分别是哪种几何体表面的展开图 先想一想,再折一折。
2.下图中的两个图形经过折叠能否围成棱柱 先想一想,再折一折。
三、综合提升
1.下列图形分别是哪种几何体表面的展开图 先想一想,再折一折,
2.图中的两个图形经过折叠能否围成棱柱 先想一想,再折一折
3.用一张纸片,通过画一画、剪一剪、折一折,制作一个棱柱形的盒子,并与
同伴进行交流
4.请收集生活中各种各样的包装盒,并将它们沿某些棱剪开,你能得到哪些
形状的展开图 将你的成果以演示文档形式进行展示与交流。
在生活中我们常常需要将一个物体截开,如切西瓜、锯木头等(如图 1-26)
如图1-27,用一个平面去截一个几何体,截出的面叫作截面
(section)
如图1-28,用一个平面去截一个正方体,截面是什么形状
(1)截面的形状可能是三角形吗 先想一想,再试一试。
(2)截面的形状还可能是几边形
与同伴交流,用平面截一个正方体,要使截面的形状是三角形、四边
形、五边形、六边形,需要平面与正方体的几个面相交就可以得到
可以截出七边形吗
图1-29中的截面分别是什么形状
与同伴交流,截一个几何体,怎样可以截出边数不同的多边形 尝试总
结活动经验。
1、七边形的截法:
平面斜截六棱柱,从一个端面切出,
这样,在端面上有一条边,每个侧面各有一条边,共7条边;
2、八边形的截法:
平面斜截六棱柱,分别从两个端面切出,
这样,在两个端面上各有一条边,每个侧面各有一条边,共8条边.
分别指出图中几何体截面形状的标号
用一个平面去截一个几何体,如果截面的形状是长方形,那么原来的
几何体可能是什么
总结
观察立体图形
01
02
展开立体图形
03
综合提升
第一单元 丰富的图形世界
第二节 从立体图形到平面图形
(2024鲁教版)六年级上
第一单元 丰富的图形世界
第二节 从立体图形到平面图形
(2024鲁教版)六年级上
学习目标
观察立体图形
01
02
展开立体图形
03
综合提升
一、观察立体图形
在小学,我们曾经辨认过从正面、左面(或右面)和上面三个不同方向观
察同一物体时看到的物体的形状图。例如,图1-10是由大小相同的小立方块搭
成的几何体,从正面、左面、上面看到的这个几何体的形状图如图1-11所示
请你用6个大小相同的小立方块搭一个几何体,然后请同伴画出从正面
左面、上面看到的这个几何体的形状图。
一个几何体由多个大小相同的小立方块搭成,从上面和从左面看到的这
个几何体的形状图如图1-12所示,请搭出满足条件的几何体。你搭的几何体
由几个小立方块构成
我们可以依据从不同方向看到的两个形状图,尝试还原该几何体,
首先,根据从上面看到的形状图,可以摆放成“两行两列”的4个小立方块;
其次,根据从左面看到的形状图,最高有两层,因此有如图1-13所示的3种方案所以最终可以分析出该几何体可能由5个或6个小立方块构成。
(1)请你选择若干如图1-14所示的立方块和长
方块搭一个几何体,然后请同伴画出从正面、左面、
上面看到的这个几何体的形状图
(2)请你画出从正面、左面、上面看到的一个几何体(由若干如图1-14所示的立方块和长方块搭成)的形状图,然后请同
伴根据你画的形状图搭出相应的几何体。与同伴进行交流。
例
图1-15是由多个大小相同的小立方块所搭成的几何体
从上面看到的形状图,小正方形中的数字表示在这个位置小立方
块的个数。请画出从正面、左面看到的这个几何体的形状图
解法一:先用实物摆出这个几何体,再画出从正面、左面看到的它的形
状图(如图 1-16)。
解法二:根据从上面看到的形状图确定从正面看到的形状图有3列,从
左面看到的形状图有2行,再根据小正方形中的数字确定每行每列小立方块的个数。
1.用5个大小相同的小立方块分别搭成如图所示的几何体。请你用自己
的方式描述一下每个几何体的具体形状。
2.一个几何体由多个大小相同的小立方块搭成,从上面观察这个几何
体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小
立方块的个数。请画出从正面、左面看到的这个几何体的形状图
二、立体图形展开
还记得小学学过的正方体表面的展开图吗
将如图1-17所示的正方体沿图中红色的棱剪开,请画出它
的展开图
将一个正方体的表面沿某些棱剪开,展开成一个平面图形(展开后每个
面至少有一条边与其他面相连),你能得到哪些形状的展开图
(1)观察正方体的展开图,原正方体中未剪开的棱有几条 剪开的棱有
几条
(2)你能得到图1-18中的展开图吗
图1-19中的图形经过折叠能否围成一个正方体 你是如何判断的 与同
伴进行交流。
图1-20中的图形经过折叠可以围成一个正方体形的盒子。折好以后,与
1”面相邻的面是什么 相对的面是什么 先想一想,再折一折,看看你的
想法是否正确。
1.下面哪个图形经过折叠可以得到正方体
2.将正方体的表面分别标上数字1,2,3,4,5,6,使它的任意两个相对面
上的数字之和为 7。将它沿某些棱剪开,能得到下面的展开图吗
3.在图中增加1个大小相同的小正方形,使所得图形经
过折叠能够围成一个正方体。先想一想,再试一试。
将图1-21中的棱柱沿某些棱剪开,你能得到哪些形状的展开图 与同伴
进行交流。
和正方体一样,我们沿着棱柱的某些棱剪开,就得到了它的展开图。由
于剪开的方式不一样,我们得到的展开图也就不一样。
图1-22是三棱柱的部分展开图。
与同伴交流四棱柱的展开图、五棱柱的展开图,
直棱柱的展开图是由两个相同的多边形(底面)和一些长方形(侧面
按照不同的方式组合而成的。
(1)如图1-23,哪些图形经过折叠可以围成一个棱柱 先想一想,再折一折。
(2)适当修改图1-23中不能围成棱柱的图形,使所得图形能围成一个棱柱。
一个长方体的长、宽、高分别为5cm,4cm,3cm,请画出它的展开图
并与同伴进行交流。
(1)按照图1-24所示的方法把无底面的圆柱、圆锥的侧面展开,会得
到什么图形 先想一想,再做一做。
2)你的想法是否正确
如图1-25,圆柱的侧面展开图是长方形,圆锥的侧面展开图是扇形
在展开与折叠的活动中,你积累了哪些经验
1.下列图形分别是哪种几何体表面的展开图 先想一想,再折一折。
2.下图中的两个图形经过折叠能否围成棱柱 先想一想,再折一折。
三、综合提升
1.下列图形分别是哪种几何体表面的展开图 先想一想,再折一折,
2.图中的两个图形经过折叠能否围成棱柱 先想一想,再折一折
3.用一张纸片,通过画一画、剪一剪、折一折,制作一个棱柱形的盒子,并与
同伴进行交流
4.请收集生活中各种各样的包装盒,并将它们沿某些棱剪开,你能得到哪些
形状的展开图 将你的成果以演示文档形式进行展示与交流。
在生活中我们常常需要将一个物体截开,如切西瓜、锯木头等(如图 1-26)
如图1-27,用一个平面去截一个几何体,截出的面叫作截面
(section)
如图1-28,用一个平面去截一个正方体,截面是什么形状
(1)截面的形状可能是三角形吗 先想一想,再试一试。
(2)截面的形状还可能是几边形
与同伴交流,用平面截一个正方体,要使截面的形状是三角形、四边
形、五边形、六边形,需要平面与正方体的几个面相交就可以得到
可以截出七边形吗
图1-29中的截面分别是什么形状
与同伴交流,截一个几何体,怎样可以截出边数不同的多边形 尝试总
结活动经验。
1、七边形的截法:
平面斜截六棱柱,从一个端面切出,
这样,在端面上有一条边,每个侧面各有一条边,共7条边;
2、八边形的截法:
平面斜截六棱柱,分别从两个端面切出,
这样,在两个端面上各有一条边,每个侧面各有一条边,共8条边.
分别指出图中几何体截面形状的标号
用一个平面去截一个几何体,如果截面的形状是长方形,那么原来的
几何体可能是什么
总结
观察立体图形
01
02
展开立体图形
03
综合提升
第一单元 丰富的图形世界
第二节 从立体图形到平面图形
(2024鲁教版)六年级上
同课章节目录
