第六单元 多边形的面积 单元综合试题 2024--2025学年小学数学人教版五年级上册
文档属性
| 名称 | 第六单元 多边形的面积 单元综合试题 2024--2025学年小学数学人教版五年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 328.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六单元 多边形的面积 单元综合试题
2024--2025学年小学数学人教版五年级上册
一、选择题
1.用两个( )的三角形能拼成一个平行四边形或长方形。
A.面积相等 B.等底等高 C.完全一样
2.周长相等的正方形和平行四边形,它们的面积比较,( )。
A.正方形面积大 B.平行四边形面积大 C.无法确定
3.下图所示的平行四边形中,阴影部分的面积与空白部分的面积相比较( )。
A.阴影部分面积大 B.空白部分面积大 C.空白部分和阴影部分的面积一样大
4.如图,平行四边形底边中点是A,它的面积是12dm2,涂色部分面积是( )dm2。
A.6 B.4 C.3
5.在下面的梯形中剪去一个面积最大的平行四边形(其中一组对边在梯形上、下底边上),剩下的面积是( )dm2。(单位:dm)
A.1 B.2 C.3
6.一个平行四边形的底和高同时乘3,面积会乘( )。
A.3 B.6 C.9
7.一个三角形和一个平行四边形等底等高,这个平行四边形的面积比这个三角形的面积大2.6m2,这个平行四边形的面积是( )m2。
A.7.8 B.3.9 C.5.2
8.如果一个三角形的底和高都扩大到原来的10倍,那么它的面积( )。
A.不变 B.扩大到原来的10倍 C 扩大到原来的100倍
二、填空题
9.一个三角形,底是5cm,高是3cm,这个三角形的面积是( )cm2。
10.一个平行四边形的底是1米,高是8分米,它的面积是( )平方分米。
11.《九章算术》卷一记载这样一道数学题:今有邪田一头广三十步,一头广四十二步,正从六十四步,问为田几何?意思是:今有直角梯形田,上底长30步,下底长42步,底边上的高长64步。这块田的面积是( )平方步。
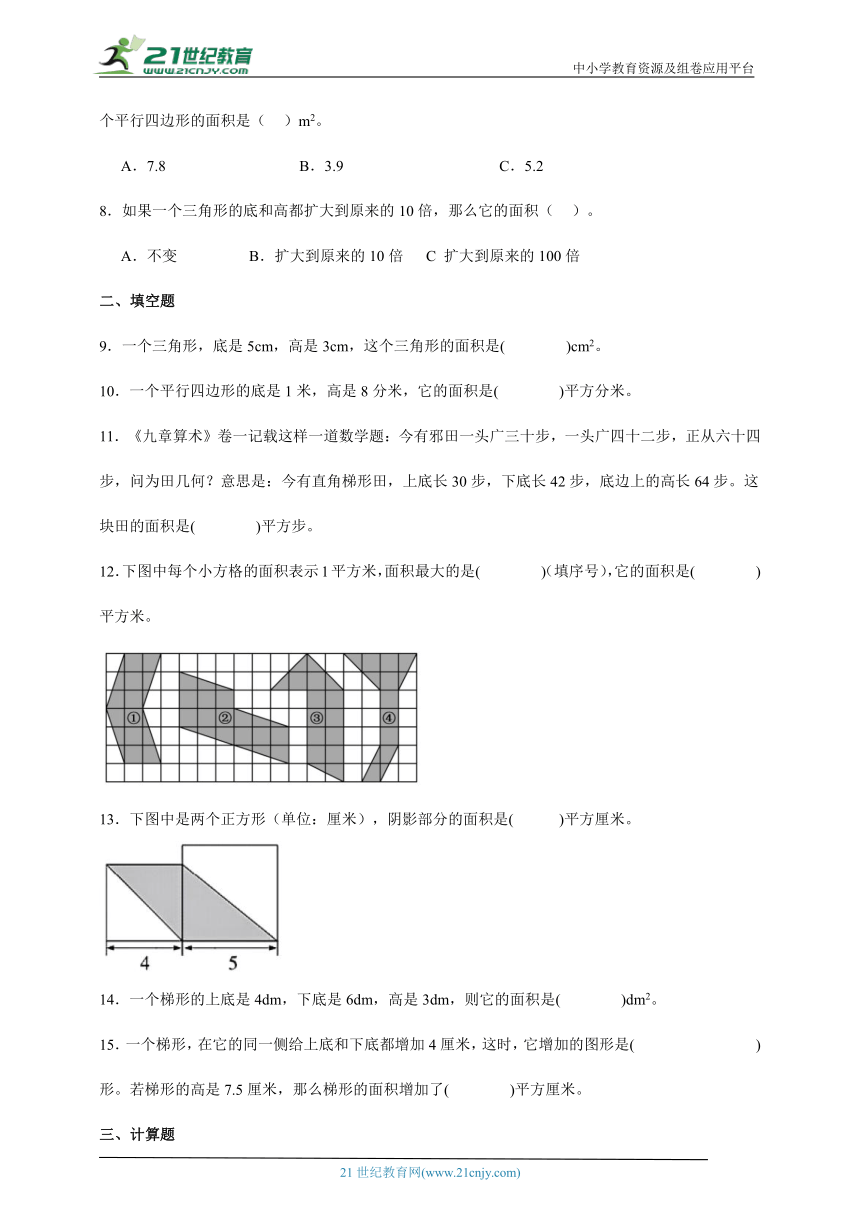
12.下图中每个小方格的面积表示1平方米,面积最大的是( )(填序号),它的面积是( )平方米。
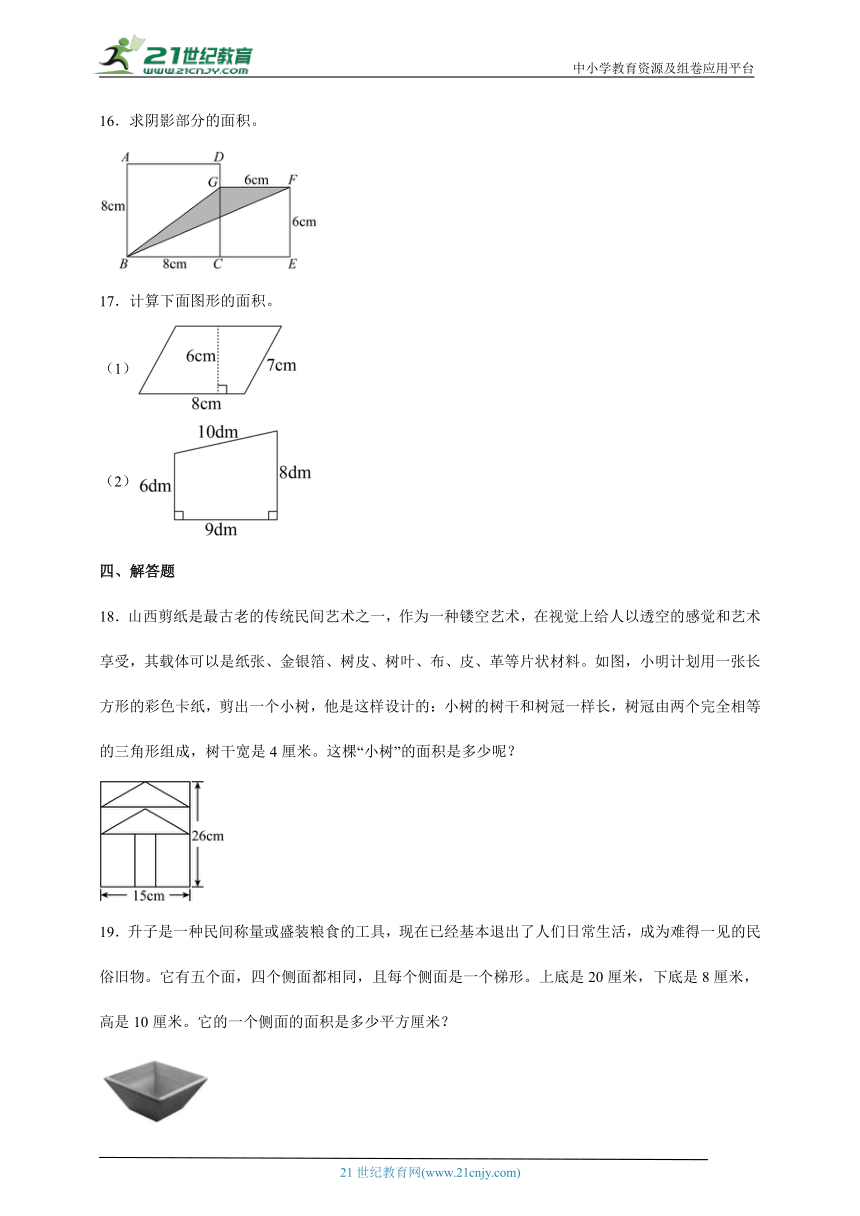
13.下图中是两个正方形(单位:厘米),阴影部分的面积是( )平方厘米。
14.一个梯形的上底是4dm,下底是6dm,高是3dm,则它的面积是( )dm2。
15.一个梯形,在它的同一侧给上底和下底都增加4厘米,这时,它增加的图形是( )形。若梯形的高是7.5厘米,那么梯形的面积增加了( )平方厘米。
三、计算题
16.求阴影部分的面积。
17.计算下面图形的面积。
(1)
(2)
四、解答题
18.山西剪纸是最古老的传统民间艺术之一,作为一种镂空艺术,在视觉上给人以透空的感觉和艺术享受,其载体可以是纸张、金银箔、树皮、树叶、布、皮、革等片状材料。如图,小明计划用一张长方形的彩色卡纸,剪出一个小树,他是这样设计的:小树的树干和树冠一样长,树冠由两个完全相等的三角形组成,树干宽是4厘米。这棵“小树”的面积是多少呢?
19.升子是一种民间称量或盛装粮食的工具,现在已经基本退出了人们日常生活,成为难得一见的民俗旧物。它有五个面,四个侧面都相同,且每个侧面是一个梯形。上底是20厘米,下底是8厘米,高是10厘米。它的一个侧面的面积是多少平方厘米?
20.2023年9月23日晚,第十九届亚洲运动会开幕式在浙江省杭州市隆重举行,国家主席习近平出席开幕式并宣布本届亚运会开幕。杭州市为美化环境,钱塘江公园靠江堤边围成一个梯形地,种上了杭州市市花桂花,形成了一座桂花园,如图,已知围桂花园的篱笆长48米,这个花园的面积是多少平方米?
21.我国著名的数学家赵爽,早在公元3世纪,就把四个完全一样的直角三角形拼成个大的正方形(如下图),这个图被称为赵爽弦图。
(1)计算这个三角形的面积。
(2)计算这个三角形斜边上的高。
(3)赵爽弦图中间的小正方形面积是多少平方厘米?
22.有一块三角形的铁皮,量得它的底是8.4分米,高比底短3.2分米。如果这种铁皮每平方米的售价是150元,那么买这块铁皮需要多少钱?
23.王裁缝做纱巾,做一个纱巾需要一块底45厘米,高32厘米的平行四边形布料。做30个这样的纱巾,共需布料多少平方厘米?
参考答案:
1.C
因为拼组平行四边形时,平行四边形的两组对边平行且相等,且有公共边,所以只有两个完全一样的三角形才能拼成一个平行四边形。
A.如图:
6×3÷2=9(cm2)
9×2÷2=9(cm2)
所以,两个三角形的面积相等,但形状不一样时,不能拼成一个平行四边形;
B.如图:
4×2÷2=4(cm2)
所以,等底等高的两个三角形面积相等,但形状不一样时,不能拼成一个平行四边形;
C.如图:
所以,可用两个完全一样的三角形能拼成一个平行四边形或长方形。
2.A
周长相等的正方形和平行四边形,假设正方形与平行四边形的四条边分别相等,根据,平行四边形的面积=底×高,平行四边形的高一定小于正方形的边长,所以正方形的面积大于平行四边形的面积。据此解答。
周长相等的正方形和平行四边形,正方形的面积大于平行四边形的面积。
故答案为:A
3.C
阴影部分是三个三角形的面积和,这三个三角形底的和等于平行四边形的底,高等于平行四边形的高,所以这三个阴影三角形的面积和等于平行四边形的面积的一半,空白部分的面积也等于平行四边形面积的一半。
由分析可知:阴影部分的面积等于平行四边形面积的一半,所以阴影部分的面积与空白部分的面积相等。
4.C
当一个三角形与一个平行四边形等底等高时,根据平行四边形的面积=底×高,三角形的面积=底×高÷2,可知这个三角形的面积是这个平行四边形面积的一半。据题意可知,图中涂色部分三角形的底是平行四边形的底的一半,则涂色部分三角形的面积是平行四边形面积的一半的一半,据此计算解答即可。
(dm2)
涂色部分面积是3dm2。
5.A
根据题意,在梯形中剪去一个面积最大的平行四边形,如下图,那么平行四边形的底是2dm、高是2dm;根据梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,代入数据计算,分别求出梯形的面积与平行四边形的面积,再相减即是剩下的面积。
(2+3)×2÷2-2×2
=5×2÷2-2×2
=5-4
=1(dm2)
剩下的面积是1dm2。
6.C
根据平行四边形的面积=底×高,以及积的变化规律可知,一个平行四边形的底和高同时乘3,则面积会乘(3×3),据此解答。
积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几。
3×3=9
一个平行四边形的底和高同时乘3,面积会乘9。
7.C
根据等底等高的平行四边形的面积是三角形的面积的2倍,把三角形的面积看成1份,则平行四边形的面积是2份,则相差(2-1)份,由此可得,平行四边形的面积比三角形大的面积就是三角形的面积,进而列式为:2.6×2,计算即可求出平行四边形的面积。
2-1=1(份)
2.6×2=5.2(m2)
这个平行四边形的面积是5.2m2。
8.C
根据三角形的面积=底×高÷2,以及积的变化规律可知,三角形的底和高都扩大到原来的10倍,则三角形的面积扩大到原来的(10×10)倍。
10×10=100
如果一个三角形的底和高都扩大到原来的10倍,那么它的面积扩大到原来的100倍。
9.7.5
根据三角形的面积公式:S=ah÷2,据此代入数值进行计算即可。
5×3÷2
=15÷2
=7.5(cm2)
则这个三角形的面积是7.5cm2。
10.80
从题意可知:先将1米换算成10分米。再根据平行四边形的面积=底×高,用10×8即可求出这个平行四边形的面积。据此解答。
1米=10分米
10×8=80(平方分米)
一个平行四边形的底是1米,高是8分米,它的面积是80平方分米。
11.2304
求直角梯形田的面积,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可解答。
(30+42)×64÷2
=72×64÷2
=4608÷2
=2304(平方步)
即这块田的面积是2304平方步。
12. ② 15
将图形采用合并、平移、割补、分割的办法,将不规则的图形转化为规则的图形如正方形、长方形等,然后再利用公式求解,从而使问题得到解决。
如图:
①将左边的三角形平移到右边,可以化为一个长为6米,宽为2米的长方形面积为
6×2=12(平方米)
②可分为一个底为3米,高为3米的平行四边形和一个底为2米,高为3米的平行四边形,面积为:
3×3+2×3
=9+6
=15(平方米)
③可分为一个底为4米,高为2米的三角形和一个上底为4米,下底为5米,高为2米的梯形,面积为:
4×2÷2+(4+5)×2÷2
=8÷2+9×2÷2
=4+18÷2
=4+9
=13(平方米)
④可分为一个上底为1米,下底为4米,高为2米的梯形;一个长为3米,宽为1米的长方形和一个底为1米,高为2米的平行四边形,面积为:
(1+4)×2÷2+3×l+1×2
=5×2÷2+3+2
=5+3+2
=8+2
=10(平方米)
10<12<13<15
面积最大的是②,它的面积是15平方米。
13.18
阴影部分的面积等于两个三角形的面积的和,小三角形的底和高就是小正方形的边长,大三角形的底是大正方形的边长,高是小正方形的边长。根据三角形的面积公式,求出两个三角形的面积,再相加即可得解。
(平方厘米)
阴影部分的面积是18平方厘米。
14.15
已知梯形的上底、下底和高,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,求出它的面积。
(4+6)×3÷2
=10×3÷2
=30÷2
=15(dm2)
它的面积是15dm2。
15. 平行四边 30
如下图,在梯形的同一侧给上底和下底都增加4厘米,增加的是一个底为4厘米,高为7.5厘米的平行四边形;根据平行四边形的面积=底×高,代入数据计算,即可求出梯形增加的面积。
如图:
一个梯形,在它的同一侧给上底和下底都增加4厘米,这时,它增加的图形是平行四边形。
4×7.5=30(平方厘米)
梯形的面积增加了30平方厘米。
16.18 cm2
根据三角形的面积=底×高÷2,求解即可。
6×6÷2
=36÷2
=18(cm2)
阴影部分的面积是18cm2。
17.(1)48cm2
(2)63dm2
(1)这是个平行四边形,平行四边形的面积=底×高,其中底边长8cm,底边上的高是6cm。
(2)这是一个直角梯形,梯形的面积=(上底+下底)×高÷2,其中上底长6dm,下底长8dm,高是9dm。
(1)8×6=48(cm2)
(2)(6+8)×9÷2
=14×9÷2
=126÷2
=63(dm2)
18.149.5平方厘米
树干和树冠一共长26厘米,树干和树冠一样长,因此树干的长度等于26÷2,树干是长方形,树干的面积=长×宽,宽是4厘米,代入数据即可计算。树冠是两个完全相同的三角形,三角形的底是15厘米,三角形的高是树冠高的一半,树冠的高和树干的长一样等于26÷2。根据三角形的面积=底×高÷2计算。小树的面积=树干的面积+三角形的面积×2。
26÷2=13(厘米)
13×4=52(平方厘米)
13÷2=6.5(厘米)
15×6.5÷2
=97.5÷2
=48.75(平方厘米)
52+48.75×2
=52+97.5
=149.5(平方厘米)
答:这棵“小树”的面积是149.5平方厘米。
19.140平方厘米
根据梯形的面积公式:面积=(上底+下底)×高÷2,代入数据,即可解答。
(20+8)×10÷2
=28×10÷2
=280÷2
=140(平方厘米)
答:它的一个侧面的面积是140平方厘米。
20.256平方米
因为靠江堤边围成一个梯形,这个梯形是一个直角梯形,篱笆所围的长度=上底+下底+高,则上底+下底=篱笆长-高。直角梯形的面积=(上底+下底)×高÷2=(篱笆长-高)×高÷2。
=
=
=(平方米)
答:这个花园的面积是256平方米。
21.(1)6平方厘米
(2)2.4厘米
(3)1平方厘米
(1)三角形面积=底×高÷2,根据图片信息可知道直角三角形的直角边分别3cm和4cm,可以为它的底和高,即可求出面积;
(2)根据三角形面积=底×高÷2,那么,高=三角形面积÷底×2,据此列式即可求出;
(3)据图片分析可知,大正方形边长为5cm,大正方形面积减去四个三角形面积就是中间小正方形面积,据此列式解答即可。
(1)3×4÷2
=12÷2
=6(cm2)
答:这个三角形的面积为6平方厘米。
(2)三角形面积为6cm2,斜边为5cm,求斜边高可列式为:
6÷5×2
=1.2×2
=2.4(cm)
答:这个三角形斜边上的高为2.4厘米。
(3)5×5-4×6
=25-24
=1(cm2)
答:赵爽弦图中间的小正方形面积是1平方厘米。
22.32.76元
已知三角形的高比底短3.2分米,用三角形的底减去3.2,求出三角形的高;
根据三角形的面积=底×高÷2,求出三角形的面积,并根据进率“1平方米=100平方分米”换算单位;
最后用这种铁皮每平方米的售价乘铁皮的面积,求出买这块铁皮需要的钱数。
三角形的高:
8.4-3.2=5.2(分米)
三角形的面积:
8.4×5.2÷2
=43.68÷2
=21.84(平方分米)
21.84平方分米=0.2184平方米
150×0.2184=32.76(元)
答:买这块铁皮需要32.76元。
23.43200平方厘米
根据公式:平行四边形的面积=底×高,求出做一个纱巾所需布料的面积,然后再乘要做的纱巾数量,就能得到总共需要的布料面积。
45×32×30=43200(平方厘米)
答:做30个这样的纱巾,共需布料43200平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六单元 多边形的面积 单元综合试题
2024--2025学年小学数学人教版五年级上册
一、选择题
1.用两个( )的三角形能拼成一个平行四边形或长方形。
A.面积相等 B.等底等高 C.完全一样
2.周长相等的正方形和平行四边形,它们的面积比较,( )。
A.正方形面积大 B.平行四边形面积大 C.无法确定
3.下图所示的平行四边形中,阴影部分的面积与空白部分的面积相比较( )。
A.阴影部分面积大 B.空白部分面积大 C.空白部分和阴影部分的面积一样大
4.如图,平行四边形底边中点是A,它的面积是12dm2,涂色部分面积是( )dm2。
A.6 B.4 C.3
5.在下面的梯形中剪去一个面积最大的平行四边形(其中一组对边在梯形上、下底边上),剩下的面积是( )dm2。(单位:dm)
A.1 B.2 C.3
6.一个平行四边形的底和高同时乘3,面积会乘( )。
A.3 B.6 C.9
7.一个三角形和一个平行四边形等底等高,这个平行四边形的面积比这个三角形的面积大2.6m2,这个平行四边形的面积是( )m2。
A.7.8 B.3.9 C.5.2
8.如果一个三角形的底和高都扩大到原来的10倍,那么它的面积( )。
A.不变 B.扩大到原来的10倍 C 扩大到原来的100倍
二、填空题
9.一个三角形,底是5cm,高是3cm,这个三角形的面积是( )cm2。
10.一个平行四边形的底是1米,高是8分米,它的面积是( )平方分米。
11.《九章算术》卷一记载这样一道数学题:今有邪田一头广三十步,一头广四十二步,正从六十四步,问为田几何?意思是:今有直角梯形田,上底长30步,下底长42步,底边上的高长64步。这块田的面积是( )平方步。
12.下图中每个小方格的面积表示1平方米,面积最大的是( )(填序号),它的面积是( )平方米。
13.下图中是两个正方形(单位:厘米),阴影部分的面积是( )平方厘米。
14.一个梯形的上底是4dm,下底是6dm,高是3dm,则它的面积是( )dm2。
15.一个梯形,在它的同一侧给上底和下底都增加4厘米,这时,它增加的图形是( )形。若梯形的高是7.5厘米,那么梯形的面积增加了( )平方厘米。
三、计算题
16.求阴影部分的面积。
17.计算下面图形的面积。
(1)
(2)
四、解答题
18.山西剪纸是最古老的传统民间艺术之一,作为一种镂空艺术,在视觉上给人以透空的感觉和艺术享受,其载体可以是纸张、金银箔、树皮、树叶、布、皮、革等片状材料。如图,小明计划用一张长方形的彩色卡纸,剪出一个小树,他是这样设计的:小树的树干和树冠一样长,树冠由两个完全相等的三角形组成,树干宽是4厘米。这棵“小树”的面积是多少呢?
19.升子是一种民间称量或盛装粮食的工具,现在已经基本退出了人们日常生活,成为难得一见的民俗旧物。它有五个面,四个侧面都相同,且每个侧面是一个梯形。上底是20厘米,下底是8厘米,高是10厘米。它的一个侧面的面积是多少平方厘米?
20.2023年9月23日晚,第十九届亚洲运动会开幕式在浙江省杭州市隆重举行,国家主席习近平出席开幕式并宣布本届亚运会开幕。杭州市为美化环境,钱塘江公园靠江堤边围成一个梯形地,种上了杭州市市花桂花,形成了一座桂花园,如图,已知围桂花园的篱笆长48米,这个花园的面积是多少平方米?
21.我国著名的数学家赵爽,早在公元3世纪,就把四个完全一样的直角三角形拼成个大的正方形(如下图),这个图被称为赵爽弦图。
(1)计算这个三角形的面积。
(2)计算这个三角形斜边上的高。
(3)赵爽弦图中间的小正方形面积是多少平方厘米?
22.有一块三角形的铁皮,量得它的底是8.4分米,高比底短3.2分米。如果这种铁皮每平方米的售价是150元,那么买这块铁皮需要多少钱?
23.王裁缝做纱巾,做一个纱巾需要一块底45厘米,高32厘米的平行四边形布料。做30个这样的纱巾,共需布料多少平方厘米?
参考答案:
1.C
因为拼组平行四边形时,平行四边形的两组对边平行且相等,且有公共边,所以只有两个完全一样的三角形才能拼成一个平行四边形。
A.如图:
6×3÷2=9(cm2)
9×2÷2=9(cm2)
所以,两个三角形的面积相等,但形状不一样时,不能拼成一个平行四边形;
B.如图:
4×2÷2=4(cm2)
所以,等底等高的两个三角形面积相等,但形状不一样时,不能拼成一个平行四边形;
C.如图:
所以,可用两个完全一样的三角形能拼成一个平行四边形或长方形。
2.A
周长相等的正方形和平行四边形,假设正方形与平行四边形的四条边分别相等,根据,平行四边形的面积=底×高,平行四边形的高一定小于正方形的边长,所以正方形的面积大于平行四边形的面积。据此解答。
周长相等的正方形和平行四边形,正方形的面积大于平行四边形的面积。
故答案为:A
3.C
阴影部分是三个三角形的面积和,这三个三角形底的和等于平行四边形的底,高等于平行四边形的高,所以这三个阴影三角形的面积和等于平行四边形的面积的一半,空白部分的面积也等于平行四边形面积的一半。
由分析可知:阴影部分的面积等于平行四边形面积的一半,所以阴影部分的面积与空白部分的面积相等。
4.C
当一个三角形与一个平行四边形等底等高时,根据平行四边形的面积=底×高,三角形的面积=底×高÷2,可知这个三角形的面积是这个平行四边形面积的一半。据题意可知,图中涂色部分三角形的底是平行四边形的底的一半,则涂色部分三角形的面积是平行四边形面积的一半的一半,据此计算解答即可。
(dm2)
涂色部分面积是3dm2。
5.A
根据题意,在梯形中剪去一个面积最大的平行四边形,如下图,那么平行四边形的底是2dm、高是2dm;根据梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,代入数据计算,分别求出梯形的面积与平行四边形的面积,再相减即是剩下的面积。
(2+3)×2÷2-2×2
=5×2÷2-2×2
=5-4
=1(dm2)
剩下的面积是1dm2。
6.C
根据平行四边形的面积=底×高,以及积的变化规律可知,一个平行四边形的底和高同时乘3,则面积会乘(3×3),据此解答。
积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几。
3×3=9
一个平行四边形的底和高同时乘3,面积会乘9。
7.C
根据等底等高的平行四边形的面积是三角形的面积的2倍,把三角形的面积看成1份,则平行四边形的面积是2份,则相差(2-1)份,由此可得,平行四边形的面积比三角形大的面积就是三角形的面积,进而列式为:2.6×2,计算即可求出平行四边形的面积。
2-1=1(份)
2.6×2=5.2(m2)
这个平行四边形的面积是5.2m2。
8.C
根据三角形的面积=底×高÷2,以及积的变化规律可知,三角形的底和高都扩大到原来的10倍,则三角形的面积扩大到原来的(10×10)倍。
10×10=100
如果一个三角形的底和高都扩大到原来的10倍,那么它的面积扩大到原来的100倍。
9.7.5
根据三角形的面积公式:S=ah÷2,据此代入数值进行计算即可。
5×3÷2
=15÷2
=7.5(cm2)
则这个三角形的面积是7.5cm2。
10.80
从题意可知:先将1米换算成10分米。再根据平行四边形的面积=底×高,用10×8即可求出这个平行四边形的面积。据此解答。
1米=10分米
10×8=80(平方分米)
一个平行四边形的底是1米,高是8分米,它的面积是80平方分米。
11.2304
求直角梯形田的面积,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可解答。
(30+42)×64÷2
=72×64÷2
=4608÷2
=2304(平方步)
即这块田的面积是2304平方步。
12. ② 15
将图形采用合并、平移、割补、分割的办法,将不规则的图形转化为规则的图形如正方形、长方形等,然后再利用公式求解,从而使问题得到解决。
如图:
①将左边的三角形平移到右边,可以化为一个长为6米,宽为2米的长方形面积为
6×2=12(平方米)
②可分为一个底为3米,高为3米的平行四边形和一个底为2米,高为3米的平行四边形,面积为:
3×3+2×3
=9+6
=15(平方米)
③可分为一个底为4米,高为2米的三角形和一个上底为4米,下底为5米,高为2米的梯形,面积为:
4×2÷2+(4+5)×2÷2
=8÷2+9×2÷2
=4+18÷2
=4+9
=13(平方米)
④可分为一个上底为1米,下底为4米,高为2米的梯形;一个长为3米,宽为1米的长方形和一个底为1米,高为2米的平行四边形,面积为:
(1+4)×2÷2+3×l+1×2
=5×2÷2+3+2
=5+3+2
=8+2
=10(平方米)
10<12<13<15
面积最大的是②,它的面积是15平方米。
13.18
阴影部分的面积等于两个三角形的面积的和,小三角形的底和高就是小正方形的边长,大三角形的底是大正方形的边长,高是小正方形的边长。根据三角形的面积公式,求出两个三角形的面积,再相加即可得解。
(平方厘米)
阴影部分的面积是18平方厘米。
14.15
已知梯形的上底、下底和高,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,求出它的面积。
(4+6)×3÷2
=10×3÷2
=30÷2
=15(dm2)
它的面积是15dm2。
15. 平行四边 30
如下图,在梯形的同一侧给上底和下底都增加4厘米,增加的是一个底为4厘米,高为7.5厘米的平行四边形;根据平行四边形的面积=底×高,代入数据计算,即可求出梯形增加的面积。
如图:
一个梯形,在它的同一侧给上底和下底都增加4厘米,这时,它增加的图形是平行四边形。
4×7.5=30(平方厘米)
梯形的面积增加了30平方厘米。
16.18 cm2
根据三角形的面积=底×高÷2,求解即可。
6×6÷2
=36÷2
=18(cm2)
阴影部分的面积是18cm2。
17.(1)48cm2
(2)63dm2
(1)这是个平行四边形,平行四边形的面积=底×高,其中底边长8cm,底边上的高是6cm。
(2)这是一个直角梯形,梯形的面积=(上底+下底)×高÷2,其中上底长6dm,下底长8dm,高是9dm。
(1)8×6=48(cm2)
(2)(6+8)×9÷2
=14×9÷2
=126÷2
=63(dm2)
18.149.5平方厘米
树干和树冠一共长26厘米,树干和树冠一样长,因此树干的长度等于26÷2,树干是长方形,树干的面积=长×宽,宽是4厘米,代入数据即可计算。树冠是两个完全相同的三角形,三角形的底是15厘米,三角形的高是树冠高的一半,树冠的高和树干的长一样等于26÷2。根据三角形的面积=底×高÷2计算。小树的面积=树干的面积+三角形的面积×2。
26÷2=13(厘米)
13×4=52(平方厘米)
13÷2=6.5(厘米)
15×6.5÷2
=97.5÷2
=48.75(平方厘米)
52+48.75×2
=52+97.5
=149.5(平方厘米)
答:这棵“小树”的面积是149.5平方厘米。
19.140平方厘米
根据梯形的面积公式:面积=(上底+下底)×高÷2,代入数据,即可解答。
(20+8)×10÷2
=28×10÷2
=280÷2
=140(平方厘米)
答:它的一个侧面的面积是140平方厘米。
20.256平方米
因为靠江堤边围成一个梯形,这个梯形是一个直角梯形,篱笆所围的长度=上底+下底+高,则上底+下底=篱笆长-高。直角梯形的面积=(上底+下底)×高÷2=(篱笆长-高)×高÷2。
=
=
=(平方米)
答:这个花园的面积是256平方米。
21.(1)6平方厘米
(2)2.4厘米
(3)1平方厘米
(1)三角形面积=底×高÷2,根据图片信息可知道直角三角形的直角边分别3cm和4cm,可以为它的底和高,即可求出面积;
(2)根据三角形面积=底×高÷2,那么,高=三角形面积÷底×2,据此列式即可求出;
(3)据图片分析可知,大正方形边长为5cm,大正方形面积减去四个三角形面积就是中间小正方形面积,据此列式解答即可。
(1)3×4÷2
=12÷2
=6(cm2)
答:这个三角形的面积为6平方厘米。
(2)三角形面积为6cm2,斜边为5cm,求斜边高可列式为:
6÷5×2
=1.2×2
=2.4(cm)
答:这个三角形斜边上的高为2.4厘米。
(3)5×5-4×6
=25-24
=1(cm2)
答:赵爽弦图中间的小正方形面积是1平方厘米。
22.32.76元
已知三角形的高比底短3.2分米,用三角形的底减去3.2,求出三角形的高;
根据三角形的面积=底×高÷2,求出三角形的面积,并根据进率“1平方米=100平方分米”换算单位;
最后用这种铁皮每平方米的售价乘铁皮的面积,求出买这块铁皮需要的钱数。
三角形的高:
8.4-3.2=5.2(分米)
三角形的面积:
8.4×5.2÷2
=43.68÷2
=21.84(平方分米)
21.84平方分米=0.2184平方米
150×0.2184=32.76(元)
答:买这块铁皮需要32.76元。
23.43200平方厘米
根据公式:平行四边形的面积=底×高,求出做一个纱巾所需布料的面积,然后再乘要做的纱巾数量,就能得到总共需要的布料面积。
45×32×30=43200(平方厘米)
答:做30个这样的纱巾,共需布料43200平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
