浙江省浙南名校2024-2025学年高二上学期期中联考数学试卷(含答案)
文档属性
| 名称 | 浙江省浙南名校2024-2025学年高二上学期期中联考数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 702.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 15:48:54 | ||
图片预览




文档简介
浙江省浙南名校2024-2025学年高二上学期期中联考数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知集合,,则( )
A. B. C. D.
2.直线关于y轴对称的直线的方程为( )
A. B. C. D.
3.在空间直角坐标系中,向量,,则在上的投影向量为( )
A. B. C. D.
4.若,为两个不同的平面,m为一条直线,则下列结论正确的是( )
A.若,,则 B.若,,则
C.若,,则与相交 D.若,,则
5.已知函数,则函数的图象的对称中心的坐标为( )
A. B. C. D.
6.已知三条直线,,将平面分为六个部分,则满足条件的m的值共有( )
A.1个 B.2个 C.3个 D.无数个
7.已知抛物线过点,圆如图,过圆心的直线l与抛物线和圆分别交于P,Q,M,N,则的最小值为( )
A.4 B.5 C.6 D.9
8.已知棱长为1的正方体内接于球O,在球O与正方体之间放入一个小正方体,则小正方体的棱长的最大值为( )
A. B. C. D.
二、多项选择题
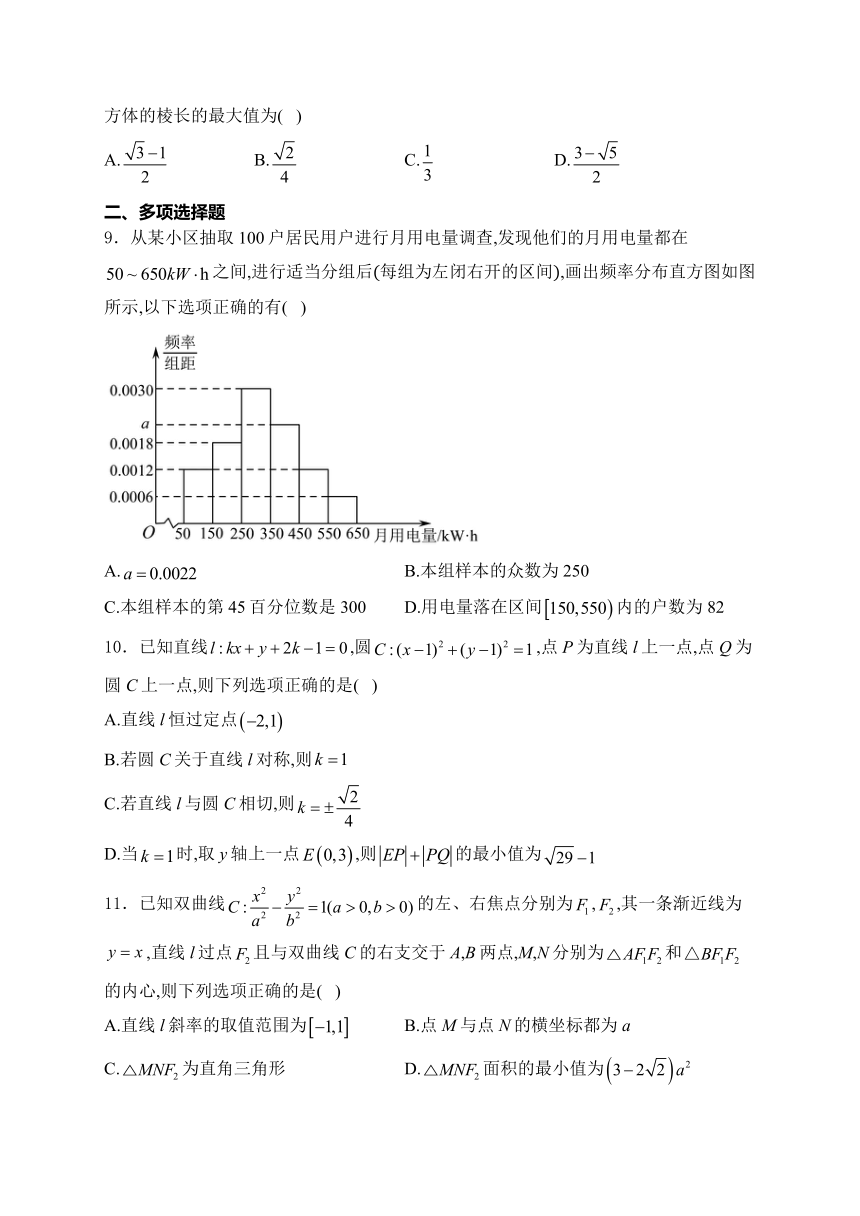
9.从某小区抽取100户居民用户进行月用电量调查,发现他们的月用电量都在之间,进行适当分组后每组为左闭右开的区间,画出频率分布直方图如图所示,以下选项正确的有( )
A. B.本组样本的众数为250
C.本组样本的第45百分位数是300 D.用电量落在区间内的户数为82
10.已知直线,圆,点P为直线l上一点,点Q为圆C上一点,则下列选项正确的是( )
A.直线l恒过定点
B.若圆C关于直线l对称,则
C.若直线l与圆C相切,则
D.当时,取y轴上一点,则的最小值为
11.已知双曲线的左、右焦点分别为,,其一条渐近线为,直线l过点且与双曲线C的右支交于A,B两点,M,N分别为和的内心,则下列选项正确的是( )
A.直线l斜率的取值范围为 B.点M与点N的横坐标都为a
C.为直角三角形 D.面积的最小值为
三、填空题
12.若A,B为两个相互独立的事件,,,则__________.
13.若函数的图象向右平移个单位后在区间上单调递减,则_____________.
14.已知正四面体的边长为2,点M,N为棱BC,AD的中点,点E,F分别为线段AM,CN上的动点,且满足,则线段EF长度的最小值为_____________.
四、解答题
15.一个不透明的盒子中装有大小和质地相同的5个小球,其中有3个黑球标号为1、2和3),2个白色球标号为4和5)若一次性从盒子中取出2个小球.
(1)写出试验的样本空间;
(2)求取出的小球恰好是1个黑球和1个白球的概率.
16.已知圆心在直线上的圆C经过两点和
(1)求圆C的方程;
(2)设点,若圆C上存在点P满足,求实数a的取值范围.
17.如图,四棱锥中,平面,,,,点E为线段的中点.
(1)证明:平面;
(2)若F为线段上一点,且,为何值时,直线与平面所成角的正弦值为
18.已知直线l是过椭圆上一点的切线.
(1)已知椭圆C的切线l过,求切线l的方程;
(2)求两焦点,到直线l的距离之积;
(3)若圆心在原点的圆与直线l也相切,且与椭圆C相交于点Q,若P,Q都在第一象限,求面积的最大值.
19.在平面直角坐标系xOy中,定义:为,两点之间的“折线距离”.
(1)已知,动点满足,求动点M所围成的图形的面积;
(2)已知Q是直线上的动点,对于任意点,求证:的最小值为
(3)已知E是函数上的动点,F为函数上的动点,求的最小值.
参考答案
1.答案:C
2.答案:A
3.答案:D
4.答案:D
5.答案:A
6.答案:C
7.答案:A
8.答案:C
9.答案:ACD
10.答案:ACD
11.答案:BC
12.答案:0.42
13.答案:
14.答案:
15.:(1);
(2)设事件A为取出的小球恰好是1个黑球和1个白球,
则
16.(1)设M,N的中点为点A,则A点坐标为,易知,
则过A点且与直线MN垂直的直线方程为,
解得,
又圆心也在直线上,
联立,解得,
即圆心为,又易知,
因此圆C的方程为;
(2)设,
,,
由题可得,
,,
化简得,
可知点P轨迹是以为圆心,以为半径的圆,
依题意可知圆C与圆有公共点,即,
解得
即实数a的取值范围为
17.(1)取线段中点G,连结,,
,G分别是线段,的中点,
且,
,,
且,
四边形为平行四边形,
,
又平面,平面,
平面;
(2)因为平面,平面,
所以,
如图,以A为原点建立空间直角坐标系.
设直线与平面所成角为,
已知,,,,
则可得,,,,
,,,,
设平面的一个法向量为,
所以,则,令,则,
为线段上一点,且,,
所以,
,
,
解得
18.(1)设,
则,
,可得,
则l为或;
(2)证明椭圆切线方程一般形式:
①当切线斜率存在时,设过点的切线方程为,
联立方程,整理得,
由可得,
所以
由韦达定理可知,即,
把代入中,得,
所以,化简得.
②当切线斜率不存在时,过的切线方程为,满足上式.
综上,椭圆上一点的切线方程为.
因为满足,所以直线,
左右焦点,到直线l距离分别为,,
;
(3)①当l斜率不存在时,此时不满足题意;
②当l斜率存在时,设,,,
其中直线,
对于圆,其中,
则,
可得,
,
令,
,
因为,所以由对勾函数性质可得,
则,即面积的最大值为.
19.(1),
则图形为正方形,其中,,,,,
所以面积为;
(2)当时,
,
当且仅当时取等号,
(由图1,,(图中,,,,与相应坐标轴垂直),
,,)
当时,
,
当且仅当时取等号;
(由图2,,(图中,,,,与相应坐标轴垂直),
,)
综上,的最小值为
(3)设,,,
当且仅当时有最小值,
为单调递减函数,
所以.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知集合,,则( )
A. B. C. D.
2.直线关于y轴对称的直线的方程为( )
A. B. C. D.
3.在空间直角坐标系中,向量,,则在上的投影向量为( )
A. B. C. D.
4.若,为两个不同的平面,m为一条直线,则下列结论正确的是( )
A.若,,则 B.若,,则
C.若,,则与相交 D.若,,则
5.已知函数,则函数的图象的对称中心的坐标为( )
A. B. C. D.
6.已知三条直线,,将平面分为六个部分,则满足条件的m的值共有( )
A.1个 B.2个 C.3个 D.无数个
7.已知抛物线过点,圆如图,过圆心的直线l与抛物线和圆分别交于P,Q,M,N,则的最小值为( )
A.4 B.5 C.6 D.9
8.已知棱长为1的正方体内接于球O,在球O与正方体之间放入一个小正方体,则小正方体的棱长的最大值为( )
A. B. C. D.
二、多项选择题
9.从某小区抽取100户居民用户进行月用电量调查,发现他们的月用电量都在之间,进行适当分组后每组为左闭右开的区间,画出频率分布直方图如图所示,以下选项正确的有( )
A. B.本组样本的众数为250
C.本组样本的第45百分位数是300 D.用电量落在区间内的户数为82
10.已知直线,圆,点P为直线l上一点,点Q为圆C上一点,则下列选项正确的是( )
A.直线l恒过定点
B.若圆C关于直线l对称,则
C.若直线l与圆C相切,则
D.当时,取y轴上一点,则的最小值为
11.已知双曲线的左、右焦点分别为,,其一条渐近线为,直线l过点且与双曲线C的右支交于A,B两点,M,N分别为和的内心,则下列选项正确的是( )
A.直线l斜率的取值范围为 B.点M与点N的横坐标都为a
C.为直角三角形 D.面积的最小值为
三、填空题
12.若A,B为两个相互独立的事件,,,则__________.
13.若函数的图象向右平移个单位后在区间上单调递减,则_____________.
14.已知正四面体的边长为2,点M,N为棱BC,AD的中点,点E,F分别为线段AM,CN上的动点,且满足,则线段EF长度的最小值为_____________.
四、解答题
15.一个不透明的盒子中装有大小和质地相同的5个小球,其中有3个黑球标号为1、2和3),2个白色球标号为4和5)若一次性从盒子中取出2个小球.
(1)写出试验的样本空间;
(2)求取出的小球恰好是1个黑球和1个白球的概率.
16.已知圆心在直线上的圆C经过两点和
(1)求圆C的方程;
(2)设点,若圆C上存在点P满足,求实数a的取值范围.
17.如图,四棱锥中,平面,,,,点E为线段的中点.
(1)证明:平面;
(2)若F为线段上一点,且,为何值时,直线与平面所成角的正弦值为
18.已知直线l是过椭圆上一点的切线.
(1)已知椭圆C的切线l过,求切线l的方程;
(2)求两焦点,到直线l的距离之积;
(3)若圆心在原点的圆与直线l也相切,且与椭圆C相交于点Q,若P,Q都在第一象限,求面积的最大值.
19.在平面直角坐标系xOy中,定义:为,两点之间的“折线距离”.
(1)已知,动点满足,求动点M所围成的图形的面积;
(2)已知Q是直线上的动点,对于任意点,求证:的最小值为
(3)已知E是函数上的动点,F为函数上的动点,求的最小值.
参考答案
1.答案:C
2.答案:A
3.答案:D
4.答案:D
5.答案:A
6.答案:C
7.答案:A
8.答案:C
9.答案:ACD
10.答案:ACD
11.答案:BC
12.答案:0.42
13.答案:
14.答案:
15.:(1);
(2)设事件A为取出的小球恰好是1个黑球和1个白球,
则
16.(1)设M,N的中点为点A,则A点坐标为,易知,
则过A点且与直线MN垂直的直线方程为,
解得,
又圆心也在直线上,
联立,解得,
即圆心为,又易知,
因此圆C的方程为;
(2)设,
,,
由题可得,
,,
化简得,
可知点P轨迹是以为圆心,以为半径的圆,
依题意可知圆C与圆有公共点,即,
解得
即实数a的取值范围为
17.(1)取线段中点G,连结,,
,G分别是线段,的中点,
且,
,,
且,
四边形为平行四边形,
,
又平面,平面,
平面;
(2)因为平面,平面,
所以,
如图,以A为原点建立空间直角坐标系.
设直线与平面所成角为,
已知,,,,
则可得,,,,
,,,,
设平面的一个法向量为,
所以,则,令,则,
为线段上一点,且,,
所以,
,
,
解得
18.(1)设,
则,
,可得,
则l为或;
(2)证明椭圆切线方程一般形式:
①当切线斜率存在时,设过点的切线方程为,
联立方程,整理得,
由可得,
所以
由韦达定理可知,即,
把代入中,得,
所以,化简得.
②当切线斜率不存在时,过的切线方程为,满足上式.
综上,椭圆上一点的切线方程为.
因为满足,所以直线,
左右焦点,到直线l距离分别为,,
;
(3)①当l斜率不存在时,此时不满足题意;
②当l斜率存在时,设,,,
其中直线,
对于圆,其中,
则,
可得,
,
令,
,
因为,所以由对勾函数性质可得,
则,即面积的最大值为.
19.(1),
则图形为正方形,其中,,,,,
所以面积为;
(2)当时,
,
当且仅当时取等号,
(由图1,,(图中,,,,与相应坐标轴垂直),
,,)
当时,
,
当且仅当时取等号;
(由图2,,(图中,,,,与相应坐标轴垂直),
,)
综上,的最小值为
(3)设,,,
当且仅当时有最小值,
为单调递减函数,
所以.
同课章节目录
