1.5 三角函数的应用(第2课时) 仰角、俯角问题 课件(共14张PPT) 2024-2025学年北师大版九年级数学下册
文档属性
| 名称 | 1.5 三角函数的应用(第2课时) 仰角、俯角问题 课件(共14张PPT) 2024-2025学年北师大版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:43:19 | ||
图片预览





文档简介
(共14张PPT)
北师版·九年级下册
5 三角函数的应用
第2课时 仰角 俯角问题
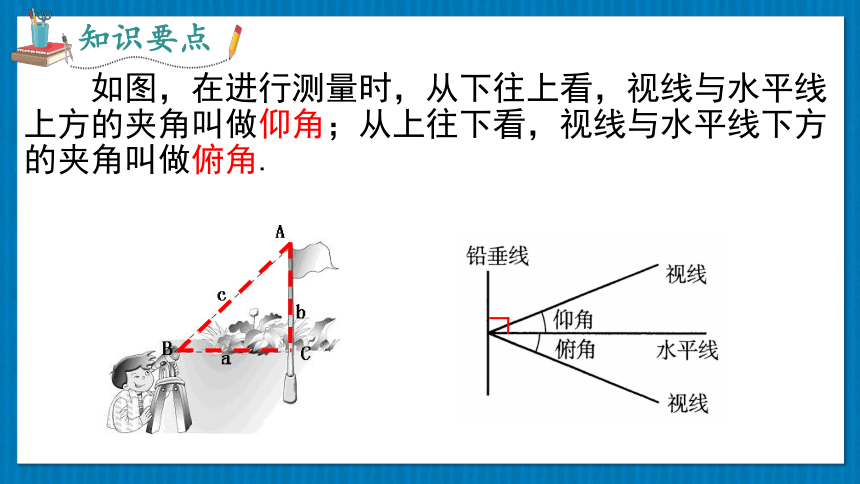
如图,在进行测量时,从下往上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
知识要点
如图,小明想测量塔CD的高度.
他在A处仰望塔顶,测得仰角为30° ,
30
再往塔的方向前进50m至B处. 测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m)
60
50 m
探索新知
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
仰角和俯角问题
2
解:如图∠DAC=30°,∠DBC=60°,AB=50m,设塔高DC=x m.
Rt△ADC中, .
Rt△BDC中, .
∴AB=AC-BC= .
∴x= ≈43(m).
30
60
50 m
步骤小结
首先要弄清题意,结合实际问题中的示意图分清题目中的已知条件和所求结论.
找出问题中有几个直角三角形,或通过作辅助线构造直角三角形,把实际问题转化为解直角三角形的问题.
方程思想、转化思想的运用.
随堂练习
1. 如图,小明站在自家阳台上A处观测到对面大楼底部C的俯角为30°,A 处到地面B处的距离AB=30 m,则两栋楼之间的距离BC为( )
A.30 m B. m C. m D. 60 m
30 m
30
C
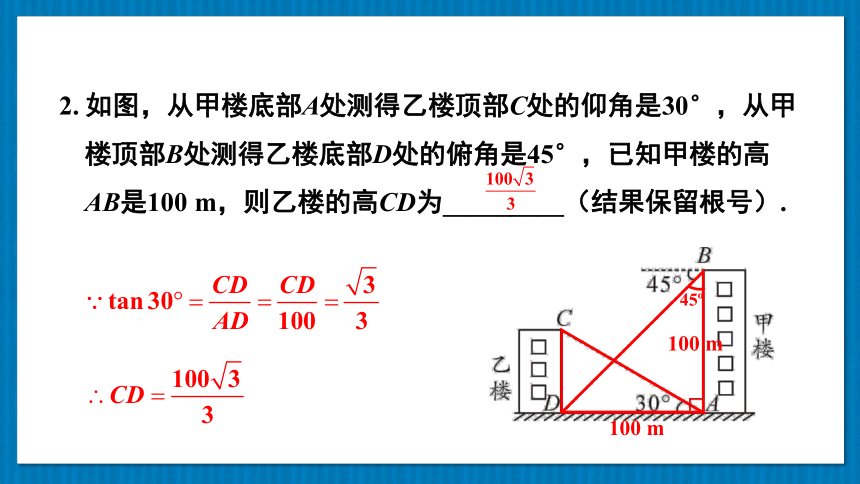
2. 如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是100 m,则乙楼的高CD为_________(结果保留根号).
45
100 m
100 m
3.[内江中考]如图,有两座建筑物DA 与CB,其中 CB的高为120 m,从DA 的顶点A测得CB顶部B的仰角为30°,测得其底部C的俯角为45°,这两座建筑物的地面距离DC为多少米?(结果保留根号)
E
解:如图所示,过点A作AE⊥BC,垂足为E.
则四边形ADCE为矩形,∴AE=DC.
设BE=x .
在Rt△ABE中,∠BAE=30°,
3.如图,有两座建筑物DA 与CB,其中 CB的高为120 m,从DA 的顶点A测得CB顶部B的仰角为30°,测得其底部C的俯角为45°,这两座建筑物的地面距离DC为多少米?(结果保留根号)
E
4. 如图,为了测量一座大桥的长度,在一架水平飞行的无人机AB的尾端A点测得桥头Р点的俯角∠α=74°,前端B点测得桥尾Q点的俯角∠β=30°,此时无人机的飞行高度AC=868 m.已知AB=1m,求这座大桥PQ的长度.(结果保留整数.参考数据:cos 74°≈0.3 ,tan74°≈ 3.5, ≈1.7, ≈1.4)
M
解:如图所示,过点B作BM⊥CQ,垂足为M.
在Rt△ACP中,∠APC=∠α=74°,
4. 如图,为了测量一座大桥的长度,在一架水平飞行的无人机AB的尾端A点测得桥头Р点的俯角∠α=74°,前端B点测得桥尾Q点的俯角∠β=30°,此时无人机的飞行高度AC=868 m.已知AB=1m,求这座大桥PQ的长度.(结果保留整数.参考数据:cos 74°≈0.3 ,tan74°≈ 3.5, ≈1.7, ≈1.4)
M
在Rt△BMQ中,∠BQM=∠β=30°,
答:这座大桥PQ的长度约为1229m.
4. 如图,一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m. 在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果精确到0.01m)
解:在Rt△CBD中,∵BC=5tan40°≈4.195(m),
∴EB=EC+CB=2+4.195=6.195(m).
在Rt△EBD中,
∴钢缆ED的长度约为7.96m.
课堂小结
通过本节课的学习,你有哪些收获?
数学源于生活 又服务于生活
课后练习
P20-21
随堂练习+习题1.6
北师版·九年级下册
5 三角函数的应用
第2课时 仰角 俯角问题
如图,在进行测量时,从下往上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
知识要点
如图,小明想测量塔CD的高度.
他在A处仰望塔顶,测得仰角为30° ,
30
再往塔的方向前进50m至B处. 测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m)
60
50 m
探索新知
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
仰角和俯角问题
2
解:如图∠DAC=30°,∠DBC=60°,AB=50m,设塔高DC=x m.
Rt△ADC中, .
Rt△BDC中, .
∴AB=AC-BC= .
∴x= ≈43(m).
30
60
50 m
步骤小结
首先要弄清题意,结合实际问题中的示意图分清题目中的已知条件和所求结论.
找出问题中有几个直角三角形,或通过作辅助线构造直角三角形,把实际问题转化为解直角三角形的问题.
方程思想、转化思想的运用.
随堂练习
1. 如图,小明站在自家阳台上A处观测到对面大楼底部C的俯角为30°,A 处到地面B处的距离AB=30 m,则两栋楼之间的距离BC为( )
A.30 m B. m C. m D. 60 m
30 m
30
C
2. 如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是100 m,则乙楼的高CD为_________(结果保留根号).
45
100 m
100 m
3.[内江中考]如图,有两座建筑物DA 与CB,其中 CB的高为120 m,从DA 的顶点A测得CB顶部B的仰角为30°,测得其底部C的俯角为45°,这两座建筑物的地面距离DC为多少米?(结果保留根号)
E
解:如图所示,过点A作AE⊥BC,垂足为E.
则四边形ADCE为矩形,∴AE=DC.
设BE=x .
在Rt△ABE中,∠BAE=30°,
3.如图,有两座建筑物DA 与CB,其中 CB的高为120 m,从DA 的顶点A测得CB顶部B的仰角为30°,测得其底部C的俯角为45°,这两座建筑物的地面距离DC为多少米?(结果保留根号)
E
4. 如图,为了测量一座大桥的长度,在一架水平飞行的无人机AB的尾端A点测得桥头Р点的俯角∠α=74°,前端B点测得桥尾Q点的俯角∠β=30°,此时无人机的飞行高度AC=868 m.已知AB=1m,求这座大桥PQ的长度.(结果保留整数.参考数据:cos 74°≈0.3 ,tan74°≈ 3.5, ≈1.7, ≈1.4)
M
解:如图所示,过点B作BM⊥CQ,垂足为M.
在Rt△ACP中,∠APC=∠α=74°,
4. 如图,为了测量一座大桥的长度,在一架水平飞行的无人机AB的尾端A点测得桥头Р点的俯角∠α=74°,前端B点测得桥尾Q点的俯角∠β=30°,此时无人机的飞行高度AC=868 m.已知AB=1m,求这座大桥PQ的长度.(结果保留整数.参考数据:cos 74°≈0.3 ,tan74°≈ 3.5, ≈1.7, ≈1.4)
M
在Rt△BMQ中,∠BQM=∠β=30°,
答:这座大桥PQ的长度约为1229m.
4. 如图,一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m. 在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果精确到0.01m)
解:在Rt△CBD中,∵BC=5tan40°≈4.195(m),
∴EB=EC+CB=2+4.195=6.195(m).
在Rt△EBD中,
∴钢缆ED的长度约为7.96m.
课堂小结
通过本节课的学习,你有哪些收获?
数学源于生活 又服务于生活
课后练习
P20-21
随堂练习+习题1.6
