2024-2025学年初中数学人教版九年级下册 27.1图形的相似 课件(共33张PPT)
文档属性
| 名称 | 2024-2025学年初中数学人教版九年级下册 27.1图形的相似 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 16.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:08:14 | ||
图片预览







文档简介
(共33张PPT)
27.1图形的相似
第二十七章 相似
学习目标
1.理解并掌握相似的概念;
2.会判断相似图形;
3.理解相似多边形的概念及性质;
4.根据相似多边形的概念判断两个多边形是否相似,并运用其性质进行相关的计算;
5.了解成比例线段的概念.
新知引入
汽车和它的模型
不同尺寸的照片
新知引入
不同大小的足球
不同字号排出的相同文字
观察这四组图片,你能总结出它们的特点吗?
归纳总结
形状相同,大小不相同
相似图形的概念:形状相同的图形叫做相似图形.
全等图形:形状相同,大小相同.
相似图形:形状相同,大小可以不同.
全等图形是特殊的相似图形.
探究新知
观察以下几组图形的变换过程,思考它们有什么关系?
图形的放大
图形的缩小
探究新知
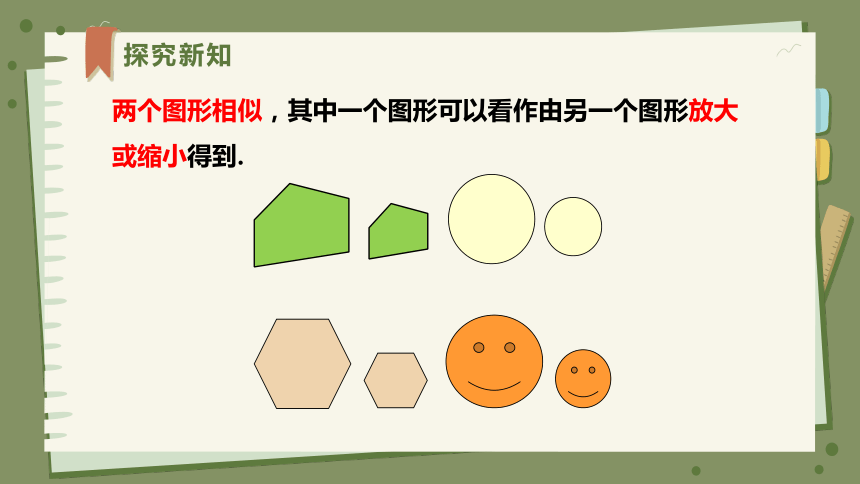
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
探究新知
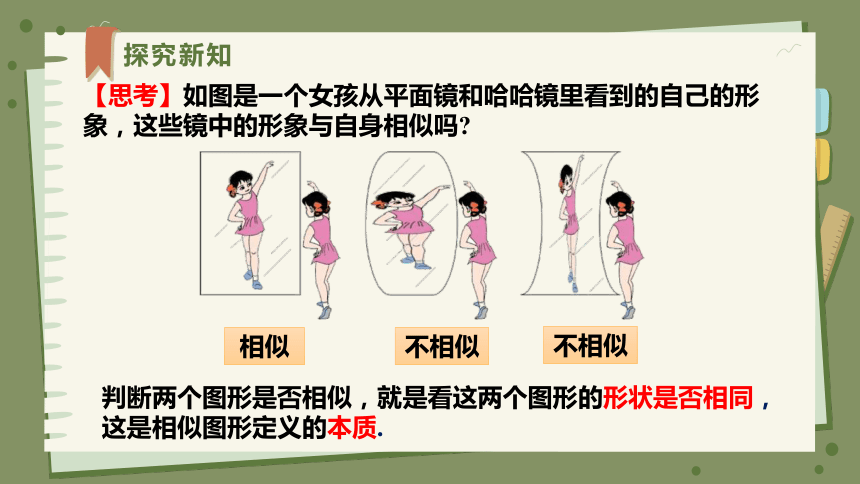
【思考】如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象与自身相似吗
判断两个图形是否相似,就是看这两个图形的形状是否相同,
这是相似图形定义的本质.
相似
不相似
不相似
探究新知
思考:图形 A 与图形 B 相似,图形 B 与图形 C 相似,请问图形 A 与图形 C 是相似图形吗?
若图形A与图形B相似,图形B与图形C相似,则图形A与图形C相似
图形的相似具有传递性
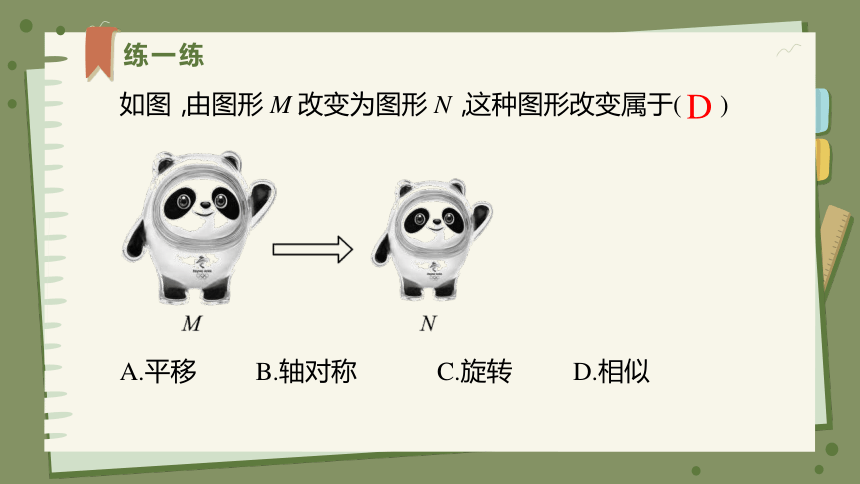
练一练
D
探究新知
由于多边形的边是线段,所以在研究相似多边形之前,先学习成比例线段的有关知识.
用同一个度量单位去度量两条线段a、b,得到它们的长度,我们把这两条线段长度的比叫做这两条线段的比,记作 或 a : b.
例如 a=2.0cm,b=1.5cm,那么 .
探究新知
对于四条线段a,b,c,d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即 (或a :b = c :d)
那么这四条线段a,b,c,d叫作成比例线段,简称比例线段.
注意:(1)两条线段的比与所采用的长度单位没有关系,在计算时要注意统一单位;线段的比是一个没有单位的正数
(2)成比例线段概念中的四条线段是有顺序的,如a、b、c、d是成比例线段与a、d、b、c是成比例线段得到的比例式是不同的
探究新知
那么 a、b、c、d 叫做组成比例的项,
a、d 叫做比例外项,
b、c 叫做比例内项,
如果
或 a:b = c:d,
若作为比例内项的两条线段相等,即a:b=b:c,则b叫做a,c的比例中项.
练一练
B
探究新知
观察下面图形的变换,思考变换前后两组多边形边有什么关系、角有什么关系?
变换前后它们的形状相同,大小不同,对应边比值相等( ),对应角相等.
归纳总结
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
探究新知
如图,两个大小不同的四边形ABCD和四边形A1B1C1D1中
D
C
B
A
则四边形ABCD和四边形A1B1C1D1相似
由相似多边形的定义可知,相似多边形的对应角相等,对应边成比例.
D1
C1
B1
A1
归纳总结
一定都相似的多边形
所有的等边三角形相似.
所有的正方形相似.
所有边数相同的正多边形相似.
所有的等腰直角三角形相似
例题练习
如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和EH 的长度 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
例题练习
解:∵ 四边形 ABCD 和 EFGH 相似,∴ 它们的对应角相等.
在四边形ABCD中,
∠β = 360°-(78°+83°+118°) = 81°.
由此可得∠α =∠C =83°,∠A =∠E = 118°.
∵ 两个四边形相似,
∴它们的对应边成比例.
由此可得
解得 x = 28.
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
归纳总结
相似
对应角相等
对应边成比例
求未知角
与未知边
建立等式
D
C
2
A
C
小结
1.相似图形的概念
形状相同的图形叫做相似图形.
2.相似多边形的概念和相似比
两个边数相同的多边形,如果它们的角分别相等,
边成比例,那么这两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
3.相似多边形的性质
相似多边形的对应角相等,对应边成比例.
谢谢同学们的聆听
27.1图形的相似
第二十七章 相似
学习目标
1.理解并掌握相似的概念;
2.会判断相似图形;
3.理解相似多边形的概念及性质;
4.根据相似多边形的概念判断两个多边形是否相似,并运用其性质进行相关的计算;
5.了解成比例线段的概念.
新知引入
汽车和它的模型
不同尺寸的照片
新知引入
不同大小的足球
不同字号排出的相同文字
观察这四组图片,你能总结出它们的特点吗?
归纳总结
形状相同,大小不相同
相似图形的概念:形状相同的图形叫做相似图形.
全等图形:形状相同,大小相同.
相似图形:形状相同,大小可以不同.
全等图形是特殊的相似图形.
探究新知
观察以下几组图形的变换过程,思考它们有什么关系?
图形的放大
图形的缩小
探究新知
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
探究新知
【思考】如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象与自身相似吗
判断两个图形是否相似,就是看这两个图形的形状是否相同,
这是相似图形定义的本质.
相似
不相似
不相似
探究新知
思考:图形 A 与图形 B 相似,图形 B 与图形 C 相似,请问图形 A 与图形 C 是相似图形吗?
若图形A与图形B相似,图形B与图形C相似,则图形A与图形C相似
图形的相似具有传递性
练一练
D
探究新知
由于多边形的边是线段,所以在研究相似多边形之前,先学习成比例线段的有关知识.
用同一个度量单位去度量两条线段a、b,得到它们的长度,我们把这两条线段长度的比叫做这两条线段的比,记作 或 a : b.
例如 a=2.0cm,b=1.5cm,那么 .
探究新知
对于四条线段a,b,c,d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即 (或a :b = c :d)
那么这四条线段a,b,c,d叫作成比例线段,简称比例线段.
注意:(1)两条线段的比与所采用的长度单位没有关系,在计算时要注意统一单位;线段的比是一个没有单位的正数
(2)成比例线段概念中的四条线段是有顺序的,如a、b、c、d是成比例线段与a、d、b、c是成比例线段得到的比例式是不同的
探究新知
那么 a、b、c、d 叫做组成比例的项,
a、d 叫做比例外项,
b、c 叫做比例内项,
如果
或 a:b = c:d,
若作为比例内项的两条线段相等,即a:b=b:c,则b叫做a,c的比例中项.
练一练
B
探究新知
观察下面图形的变换,思考变换前后两组多边形边有什么关系、角有什么关系?
变换前后它们的形状相同,大小不同,对应边比值相等( ),对应角相等.
归纳总结
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.
探究新知
如图,两个大小不同的四边形ABCD和四边形A1B1C1D1中
D
C
B
A
则四边形ABCD和四边形A1B1C1D1相似
由相似多边形的定义可知,相似多边形的对应角相等,对应边成比例.
D1
C1
B1
A1
归纳总结
一定都相似的多边形
所有的等边三角形相似.
所有的正方形相似.
所有边数相同的正多边形相似.
所有的等腰直角三角形相似
例题练习
如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和EH 的长度 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
例题练习
解:∵ 四边形 ABCD 和 EFGH 相似,∴ 它们的对应角相等.
在四边形ABCD中,
∠β = 360°-(78°+83°+118°) = 81°.
由此可得∠α =∠C =83°,∠A =∠E = 118°.
∵ 两个四边形相似,
∴它们的对应边成比例.
由此可得
解得 x = 28.
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
归纳总结
相似
对应角相等
对应边成比例
求未知角
与未知边
建立等式
D
C
2
A
C
小结
1.相似图形的概念
形状相同的图形叫做相似图形.
2.相似多边形的概念和相似比
两个边数相同的多边形,如果它们的角分别相等,
边成比例,那么这两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
3.相似多边形的性质
相似多边形的对应角相等,对应边成比例.
谢谢同学们的聆听
