2024-2025学年初中数学人教版九年级下册 26.1.2反比例函数的图象和性质(课时2)课件(共29张PPT)
文档属性
| 名称 | 2024-2025学年初中数学人教版九年级下册 26.1.2反比例函数的图象和性质(课时2)课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 20.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:07:48 | ||
图片预览





文档简介
(共29张PPT)
26.1.2反比例函数的图象和性质
(课时2)
第二十六章 反比例函数
学习目标
1. 能根据函数图象上的点的坐标求函数解析式,并能判断一个点是否在反比例函数图象上.
2.能灵活运用函数图象和性质解决一些较综合的问题;
3.掌握反比例函数的比例系数k的意义,并能应用其解决有关问题.
知识回顾
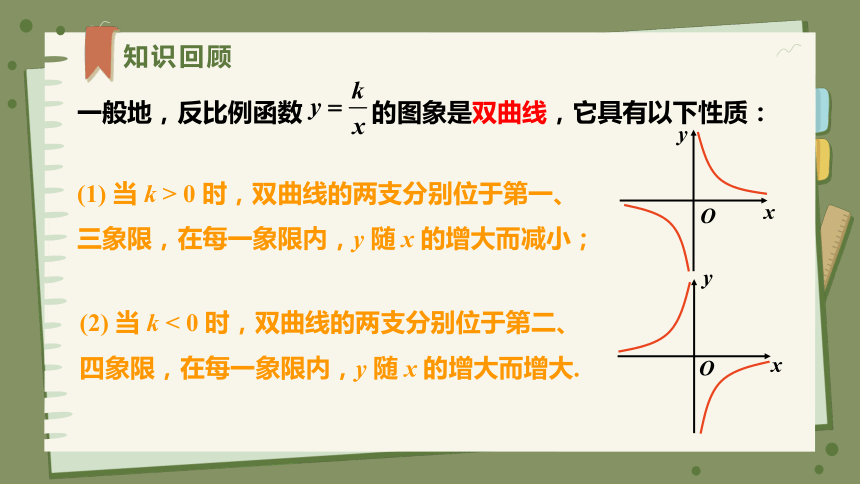
(1) 当 k > 0 时,双曲线的两支分别位于第一、三象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四象限,在每一象限内,y 随 x 的增大而增大.
一般地,反比例函数 的图象是双曲线,它具有以下性质:
O
x
y
O
x
y
探究新知
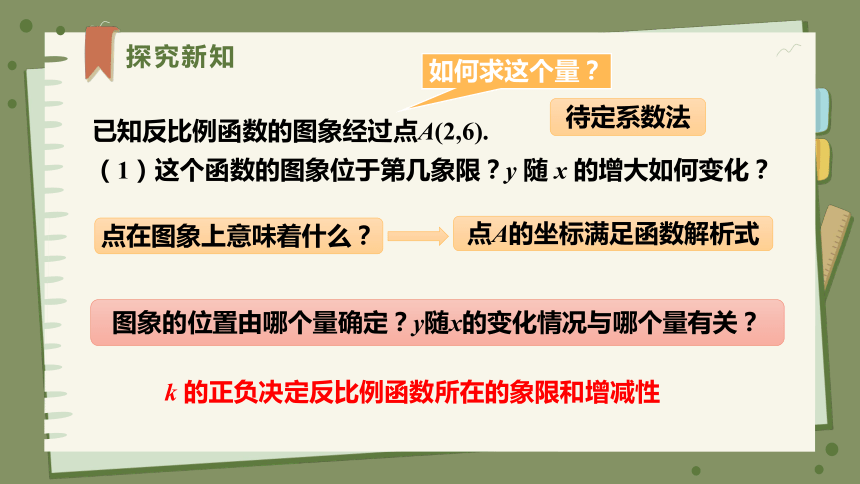
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于第几象限?y 随 x 的增大如何变化?
图象的位置由哪个量确定?y随x的变化情况与哪个量有关?
点在图象上意味着什么?
点A的坐标满足函数解析式
待定系数法
如何求这个量?
k 的正负决定反比例函数所在的象限和增减性
解:
(1)设反比例函数的解析式为 ;
∵反比例函数的图象经过点A(2,6);
∴
,解得 ;
∴函数的图象分别位于第一、三象限,
在每个象限内,y随x的增大而减小.
求反比例函数解析式时,只需要图象上一个点坐标即可.
(2)因为点 B,C 的坐标都满足该解析式,而点 D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
探究新知
(2) 点B(3,4),C( , ),D(2,5) 是否在这个函数的图象上?
你有更快捷的判断方法吗?
分析:根据 xy=k 可知,只要点的横纵坐标乘积都等于k即可.
对于点B:3×4=12 (符合k的要求),所以点B在这个函数的图象上.
对于点C: (符合k的要求),所以点B在这个函数的图象上.
对于点D:2×5=10 (不符合k的要求),所以点D不在函数的图象上.
由(1)知,k = 12.
探究新知
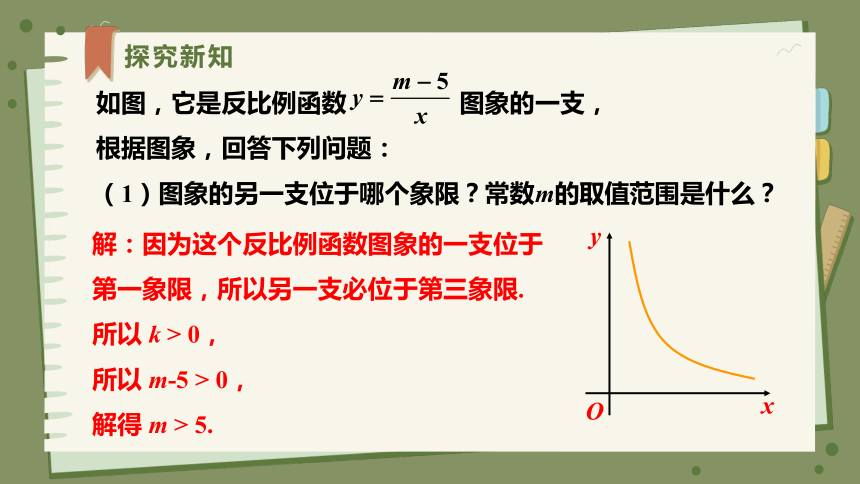
如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
O
x
y
解:因为这个反比例函数图象的一支位于第一象限,所以另一支必位于第三象限.
所以 k > 0,
所以 m-5 > 0,
解得 m > 5.
探究新知
O
x
y
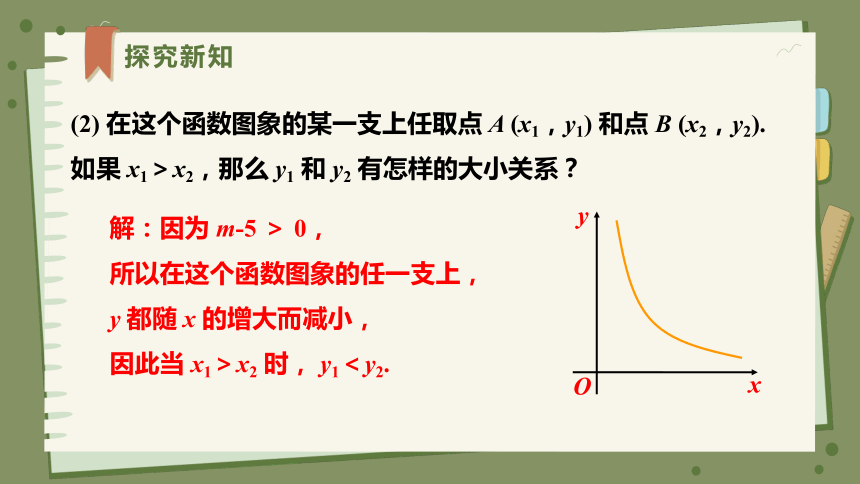
(2) 在这个函数图象的某一支上任取点 A (x1,y1) 和点 B (x2,y2). 如果 x1>x2,那么 y1 和 y2 有怎样的大小关系?
解:因为 m-5 > 0,
所以在这个函数图象的任一支上,y 都随 x 的增大而减小,
因此当 x1>x2 时, y1<y2.
探究新知
探究新知
反比例函数解析式中 k 的几何意义
1. 在反比例函数 的图象上分别取点 P,Q 向 x 轴、y 轴作垂线,与x轴,y轴围成的矩形面积分别为 S1,S2 的矩形,填写下页表格:
探究新知
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
P (2,2)
Q (4,1)
S1的值
S2的值
S1与S2的关系
猜想 S1,S2 与 k的关系
4
4
S1=S2
S1=S2=k
探究新知
2. 在反比例函数 中是否也有相同的结论?在图象上任取两点P,Q分别向x,y轴作垂线,填写表格:
y
x
O
P
Q
S1
S2
S1的值 S2的值 S1与S2的关系 猜想S1,S2与 k 的关系
P (-1,4) Q (-2,2)
4
4
S1=S2
S1 = S2= -k
探究新知
我们就 k < 0 的情况给出证明:
设点 P 的坐标为 (a,b),
∵点 P (a,b) 在函数 的图象上,
∴ ,即 ab=k.
∴ S矩形 AOBP = PB·PA = -a·b = -ab = -k;
若点 P 在第二象限,则 a<0,b>0,
若点 P 在第四象限,则 a>0,b<0,
∴ S矩形 AOBP = PB·PA = a · ( -b ) = -ab = -k.
综上,S矩形 AOBP = |k|.
y
x
O
P
A
B
B
P
A
归纳总结
点 Q 是其图象上的任意一点,作 QA 垂直于 y 轴,作QB 垂直于x 轴,矩形AOBQ的面积与 k 的关系是S矩形AOBQ = .
推理:△QAO与△QBO的面积和 k 的关系是
S△QAO=S△QBO= .
Q
对于反比例函数 ,
A
B
|k|
y
x
O
反比例函数的面积不变性
A
练一练
B
C
C
C
D
B
D
谢谢同学们的聆听
26.1.2反比例函数的图象和性质
(课时2)
第二十六章 反比例函数
学习目标
1. 能根据函数图象上的点的坐标求函数解析式,并能判断一个点是否在反比例函数图象上.
2.能灵活运用函数图象和性质解决一些较综合的问题;
3.掌握反比例函数的比例系数k的意义,并能应用其解决有关问题.
知识回顾
(1) 当 k > 0 时,双曲线的两支分别位于第一、三象限,在每一象限内,y 随 x 的增大而减小;
(2) 当 k < 0 时,双曲线的两支分别位于第二、四象限,在每一象限内,y 随 x 的增大而增大.
一般地,反比例函数 的图象是双曲线,它具有以下性质:
O
x
y
O
x
y
探究新知
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于第几象限?y 随 x 的增大如何变化?
图象的位置由哪个量确定?y随x的变化情况与哪个量有关?
点在图象上意味着什么?
点A的坐标满足函数解析式
待定系数法
如何求这个量?
k 的正负决定反比例函数所在的象限和增减性
解:
(1)设反比例函数的解析式为 ;
∵反比例函数的图象经过点A(2,6);
∴
,解得 ;
∴函数的图象分别位于第一、三象限,
在每个象限内,y随x的增大而减小.
求反比例函数解析式时,只需要图象上一个点坐标即可.
(2)因为点 B,C 的坐标都满足该解析式,而点 D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上.
探究新知
(2) 点B(3,4),C( , ),D(2,5) 是否在这个函数的图象上?
你有更快捷的判断方法吗?
分析:根据 xy=k 可知,只要点的横纵坐标乘积都等于k即可.
对于点B:3×4=12 (符合k的要求),所以点B在这个函数的图象上.
对于点C: (符合k的要求),所以点B在这个函数的图象上.
对于点D:2×5=10 (不符合k的要求),所以点D不在函数的图象上.
由(1)知,k = 12.
探究新知
如图,它是反比例函数 图象的一支,
根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
O
x
y
解:因为这个反比例函数图象的一支位于第一象限,所以另一支必位于第三象限.
所以 k > 0,
所以 m-5 > 0,
解得 m > 5.
探究新知
O
x
y
(2) 在这个函数图象的某一支上任取点 A (x1,y1) 和点 B (x2,y2). 如果 x1>x2,那么 y1 和 y2 有怎样的大小关系?
解:因为 m-5 > 0,
所以在这个函数图象的任一支上,y 都随 x 的增大而减小,
因此当 x1>x2 时, y1<y2.
探究新知
探究新知
反比例函数解析式中 k 的几何意义
1. 在反比例函数 的图象上分别取点 P,Q 向 x 轴、y 轴作垂线,与x轴,y轴围成的矩形面积分别为 S1,S2 的矩形,填写下页表格:
探究新知
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
P (2,2)
Q (4,1)
S1的值
S2的值
S1与S2的关系
猜想 S1,S2 与 k的关系
4
4
S1=S2
S1=S2=k
探究新知
2. 在反比例函数 中是否也有相同的结论?在图象上任取两点P,Q分别向x,y轴作垂线,填写表格:
y
x
O
P
Q
S1
S2
S1的值 S2的值 S1与S2的关系 猜想S1,S2与 k 的关系
P (-1,4) Q (-2,2)
4
4
S1=S2
S1 = S2= -k
探究新知
我们就 k < 0 的情况给出证明:
设点 P 的坐标为 (a,b),
∵点 P (a,b) 在函数 的图象上,
∴ ,即 ab=k.
∴ S矩形 AOBP = PB·PA = -a·b = -ab = -k;
若点 P 在第二象限,则 a<0,b>0,
若点 P 在第四象限,则 a>0,b<0,
∴ S矩形 AOBP = PB·PA = a · ( -b ) = -ab = -k.
综上,S矩形 AOBP = |k|.
y
x
O
P
A
B
B
P
A
归纳总结
点 Q 是其图象上的任意一点,作 QA 垂直于 y 轴,作QB 垂直于x 轴,矩形AOBQ的面积与 k 的关系是S矩形AOBQ = .
推理:△QAO与△QBO的面积和 k 的关系是
S△QAO=S△QBO= .
Q
对于反比例函数 ,
A
B
|k|
y
x
O
反比例函数的面积不变性
A
练一练
B
C
C
C
D
B
D
谢谢同学们的聆听
