2024-2025学年初中数学人教版九年级下册 27.2.1相似三角形的判定(课时3) 课件(共26张PPT)
文档属性
| 名称 | 2024-2025学年初中数学人教版九年级下册 27.2.1相似三角形的判定(课时3) 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:11:15 | ||
图片预览







文档简介
(共26张PPT)
27.2.1相似三角形的判定
(课时3)
第二十七章 相似
学习目标
1.理解并掌握两角分别相等的两个三角形相似的判定定理;
2.理解并掌握判定两个直角三角形相似的方法;
3.灵活应用三角形相似的判定解决数学问题.
复习巩固
目前为止,我们学习了哪些判定三角形相似的方法?
1.定义法:对应角相等,对应边成比例的三角形相似
2.平行线法:平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
3.三边成比例的两个三角形相似.
4.两边成比例且夹角相等的两个三角形相似.
探究新知
思考:类似于判定三角形全等的AAS和ASA的方法,你能得到哪些判定三角形相似的方法呢?
观察两副三角尺如图所示,其中有同样两个锐角(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.
探究新知
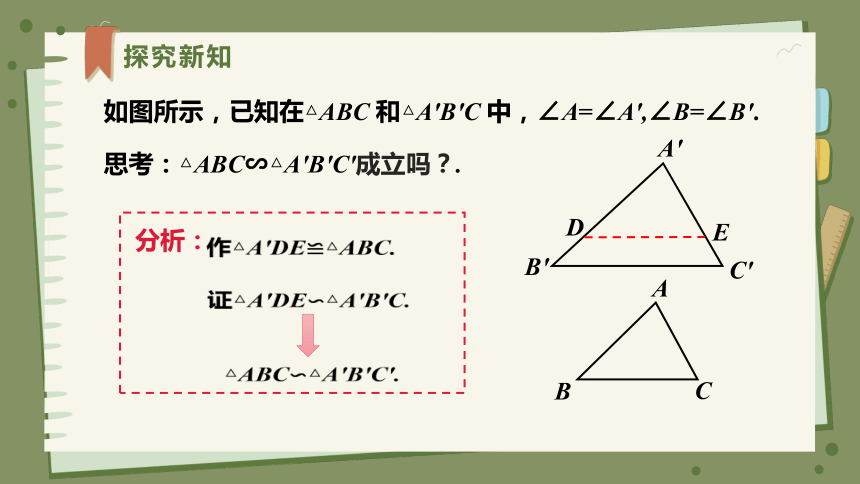
如图所示,已知在△ABC 和△A′B′C 中,∠A=∠A′,∠B=∠B′.
思考:△ABC∽△A′B′C′成立吗?.
分析:
作
证
A
B
C
A'
B'
C'
D
E
探究新知
A
B
C
A'
B'
C'
D
E
证明:在线段A′B′上截取A′D=AB,过点D作DE∥B′C′,交A′C′于点E,则可得△A′DE∽△A′B′C′.
∵DE∥B′C′,∴∠A′DE=∠B′
又∠B=∠B′,∴∠B=∠A′DE
又∵∠A=∠A′,A′D=AB
∴△A′DE≌△ABC
∴△ABC∽△A′B′C′.
归纳总结
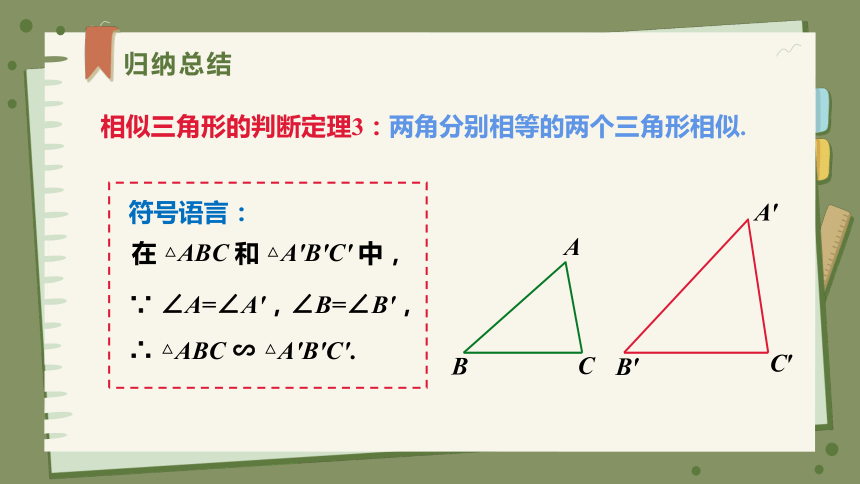
相似三角形的判断定理3:两角分别相等的两个三角形相似.
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
在 △ABC 和 △A'B'C' 中,
A
B
C
A′
C′
B′
例题练习
如图,Rt△ABC中,∠C=90°,AB=10,AC=8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D.求AD的长.
D
A
B
C
E
解:∵E =D⊥AB,∴∠EDA = 90°
又∠C = 90°,∠A =∠A,
∴△AED∽△ABC,
∴
∴
探究新知
由三角形相似的条件可知,如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似.
思考:我们知道,两个直角三角形全等可以用“HL”来判定.那么,满足斜边和一条直角边成比例的两个直角三角形相似吗?
探究新知
如图所示,在 Rt△ABC 和 Rt△A′B′C′中,∠C=90°,∠C′=90°
,求证 Rt△ABC∽Rt△A′B′C′.
C
A
A'
B
B'
C'
分析:要证Rt△ABC∽Rt△A'B'C',
可设法证明
,只需证
若设
探究新知
证明:设 = k,则 AB = kA′B′,AC = kA′C′.
由勾股定理,得
∴ .
∴ Rt△ABC ∽ Rt△A′B′C′.
∴
C
A
A'
B
B'
C'
归纳总结
斜边和一直角边成比例的两个直角三角形相似.
在 Rt△ABC 和 Rt△A′B′C′ 中,
符号语言:
∵∠C=90°,∠C′=90°
且
∴ △ABC ∽ △A′B′C′ .
C
A
A'
B
B'
C'
归纳总结
判定直角三角形相似的方法:
①一个锐角相等的两个直角三角形相似;
②两组直角边成比例的两个直角三角形相似;
③斜边和一条直角边成比例的两个直角三角形相似.
B
C
B
小结
判定三角形相似的定理:
两角分别相等的两个三角形相似..
判定直角三角形相似的方法:
①一个锐角相等的两个直角三角形相似;
②两组直角边成比例的两个直角三角形相似;
③斜边和一条直角边成比例的两个直角三角形相似.
谢谢同学们的聆听
27.2.1相似三角形的判定
(课时3)
第二十七章 相似
学习目标
1.理解并掌握两角分别相等的两个三角形相似的判定定理;
2.理解并掌握判定两个直角三角形相似的方法;
3.灵活应用三角形相似的判定解决数学问题.
复习巩固
目前为止,我们学习了哪些判定三角形相似的方法?
1.定义法:对应角相等,对应边成比例的三角形相似
2.平行线法:平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
3.三边成比例的两个三角形相似.
4.两边成比例且夹角相等的两个三角形相似.
探究新知
思考:类似于判定三角形全等的AAS和ASA的方法,你能得到哪些判定三角形相似的方法呢?
观察两副三角尺如图所示,其中有同样两个锐角(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.
探究新知
如图所示,已知在△ABC 和△A′B′C 中,∠A=∠A′,∠B=∠B′.
思考:△ABC∽△A′B′C′成立吗?.
分析:
作
证
A
B
C
A'
B'
C'
D
E
探究新知
A
B
C
A'
B'
C'
D
E
证明:在线段A′B′上截取A′D=AB,过点D作DE∥B′C′,交A′C′于点E,则可得△A′DE∽△A′B′C′.
∵DE∥B′C′,∴∠A′DE=∠B′
又∠B=∠B′,∴∠B=∠A′DE
又∵∠A=∠A′,A′D=AB
∴△A′DE≌△ABC
∴△ABC∽△A′B′C′.
归纳总结
相似三角形的判断定理3:两角分别相等的两个三角形相似.
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
在 △ABC 和 △A'B'C' 中,
A
B
C
A′
C′
B′
例题练习
如图,Rt△ABC中,∠C=90°,AB=10,AC=8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D.求AD的长.
D
A
B
C
E
解:∵E =D⊥AB,∴∠EDA = 90°
又∠C = 90°,∠A =∠A,
∴△AED∽△ABC,
∴
∴
探究新知
由三角形相似的条件可知,如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似.
思考:我们知道,两个直角三角形全等可以用“HL”来判定.那么,满足斜边和一条直角边成比例的两个直角三角形相似吗?
探究新知
如图所示,在 Rt△ABC 和 Rt△A′B′C′中,∠C=90°,∠C′=90°
,求证 Rt△ABC∽Rt△A′B′C′.
C
A
A'
B
B'
C'
分析:要证Rt△ABC∽Rt△A'B'C',
可设法证明
,只需证
若设
探究新知
证明:设 = k,则 AB = kA′B′,AC = kA′C′.
由勾股定理,得
∴ .
∴ Rt△ABC ∽ Rt△A′B′C′.
∴
C
A
A'
B
B'
C'
归纳总结
斜边和一直角边成比例的两个直角三角形相似.
在 Rt△ABC 和 Rt△A′B′C′ 中,
符号语言:
∵∠C=90°,∠C′=90°
且
∴ △ABC ∽ △A′B′C′ .
C
A
A'
B
B'
C'
归纳总结
判定直角三角形相似的方法:
①一个锐角相等的两个直角三角形相似;
②两组直角边成比例的两个直角三角形相似;
③斜边和一条直角边成比例的两个直角三角形相似.
B
C
B
小结
判定三角形相似的定理:
两角分别相等的两个三角形相似..
判定直角三角形相似的方法:
①一个锐角相等的两个直角三角形相似;
②两组直角边成比例的两个直角三角形相似;
③斜边和一条直角边成比例的两个直角三角形相似.
谢谢同学们的聆听
