2024-2025学年初中数学人教版九年级下册 27.2.2相似三角形的性质 课件(共30张PPT)
文档属性
| 名称 | 2024-2025学年初中数学人教版九年级下册 27.2.2相似三角形的性质 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 18.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:10:03 | ||
图片预览











文档简介
(共30张PPT)
27.2.2相似三角形的性质
第二十七章 相似
素养目标
1.掌握相似三角形中相应线段的比等于相似比;
2.掌握相似三角形的周长比等于相似比,面积比等于相似比的平方;
3.感受几何命题的合理性,培养学生发现问题、解决问题的能力.
重点
重难点
复习巩固
相似三角形的判定方法有哪些?
①定义:对应边 ,对应角 的两个三角形相似;
② 于三角形一边的直线与另外两边相交所构成的三角形与原三角形相似;
③三边 的两个三角形相似;
④两边 且夹角 的两个三角形相似;
⑤两角分别 的两个三角形相似;
⑥一组直角边和斜边 的两个直角三角形相似.
成比例
相等
平行
成比例
成比例
相等
相等
成比例
新课导入
三角形除了三个角,三条边外,还有哪些要素?
如果两个三角形相似,那么,对应的这些要素之间有什么关系呢?
高
中线
角平分线
周长
面积
探究新知
【探究一】如图, △ABC ∽△A′B′C′ ,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
探究新知
∴△ABD ∽ △A' B' D'
∴
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A'D'
则∠ADB =∠A' D' B' = 90°
∵△ABC ∽ △A′B′C′
∴∠B =∠B'
A
B
A'
B'
D'
D
C'
C
两角对应相等的两个三角形相似
结论:相似三角形对应高的比等于相似比
解:如图,分别作出 △ABC 和△A' B' C' 的角平分线
AD 和 A'D',则∠BAD =∠B' A' D'
∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
∴△ABD ∽△A' B' D'
∴
探究新知
两角对应相等的两个三角形相似
结论:相似三角形对应角平分线的比等于相似比
A
B
C
D
A'
B'
C'
D'
解:如图,分别作出 △ABC 和△ A′B′C′的中线 AD 和 A'D',
则
∵△ABC ∽△A′B′C′
∴∠B =∠B' ,
∴△ABD ∽△A' B' D'
∴
探究新知
两边成比例且夹角相等的两个三角形相似
结论:相似三角形对应中线的比等于相似比
A
B
C
A'
B'
C'
D'
D
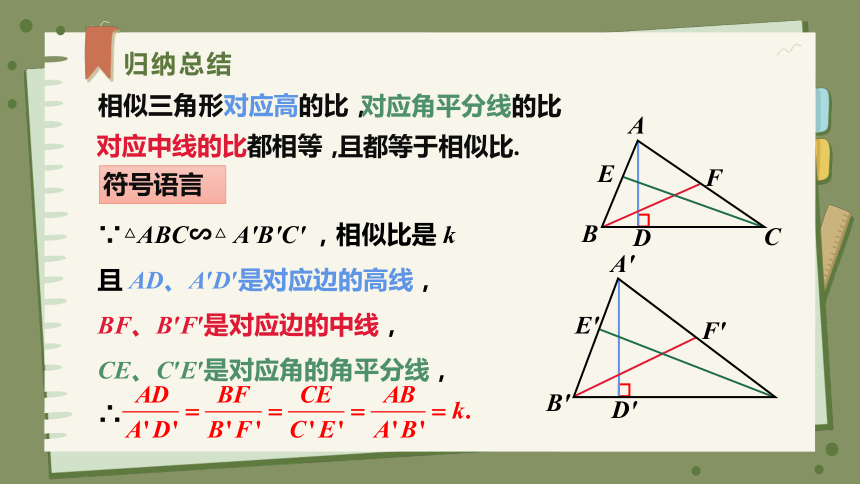
归纳总结
且都等于相似比.
A'
B'
A
B
C
D'
D
F
F'
E
E'
符号语言
相似三角形对应高的比,
对应角平分线的比
对应中线的比都相等,
∵△ABC∽△ A′B′C′ ,相似比是 k
且 AD、A′D′是对应边的高线,
BF、B′F′是对应边的中线,
CE、C′E′是对应角的角平分线,
∴
练一练
B
练一练
B
探究新知
【探究二】相似三角形的周长有什么关系呢?
解:如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB = kA'B',BC = kB'C',CA = kC'A',
从而
A
B
C
A'
B'
C'
结论:相似三角形周长的比等于相似比
探究新知
【探究三】相似三角形面积的比与相似比有什么关系?
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
探究新知
A
B
A'
B'
D'
D
C'
C
由前面的结论,得
结论:相似三角形面积的比等于相似比的平方
作三角形的高
例题练习
如图,在 △ABC 和 △DEF 中,AB = 2DE ,AC = 2DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
A
B
C
D
E
F
例题练习
A
B
C
D
E
F
解:在 △ABC 和 △DEF 中,∵ AB = 2DE,AC = 2DF,
又 ∵∠D =∠A,
∴ △DEF ∽ △ABC ,相似比为
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
∴
两边成比例且夹角相等的两个三角形相似
B
A
D
C
A
D
12
3
小结
相似三角形的性质:
1.相似三角形对应高的比,对应中线的比、对应角平分线的比都等于相似比.
2.相似三角形周长的比等于相似比.
3.相似三角形面积的比等于相似比的平方
谢谢同学们的聆听
27.2.2相似三角形的性质
第二十七章 相似
素养目标
1.掌握相似三角形中相应线段的比等于相似比;
2.掌握相似三角形的周长比等于相似比,面积比等于相似比的平方;
3.感受几何命题的合理性,培养学生发现问题、解决问题的能力.
重点
重难点
复习巩固
相似三角形的判定方法有哪些?
①定义:对应边 ,对应角 的两个三角形相似;
② 于三角形一边的直线与另外两边相交所构成的三角形与原三角形相似;
③三边 的两个三角形相似;
④两边 且夹角 的两个三角形相似;
⑤两角分别 的两个三角形相似;
⑥一组直角边和斜边 的两个直角三角形相似.
成比例
相等
平行
成比例
成比例
相等
相等
成比例
新课导入
三角形除了三个角,三条边外,还有哪些要素?
如果两个三角形相似,那么,对应的这些要素之间有什么关系呢?
高
中线
角平分线
周长
面积
探究新知
【探究一】如图, △ABC ∽△A′B′C′ ,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
探究新知
∴△ABD ∽ △A' B' D'
∴
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A'D'
则∠ADB =∠A' D' B' = 90°
∵△ABC ∽ △A′B′C′
∴∠B =∠B'
A
B
A'
B'
D'
D
C'
C
两角对应相等的两个三角形相似
结论:相似三角形对应高的比等于相似比
解:如图,分别作出 △ABC 和△A' B' C' 的角平分线
AD 和 A'D',则∠BAD =∠B' A' D'
∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
∴△ABD ∽△A' B' D'
∴
探究新知
两角对应相等的两个三角形相似
结论:相似三角形对应角平分线的比等于相似比
A
B
C
D
A'
B'
C'
D'
解:如图,分别作出 △ABC 和△ A′B′C′的中线 AD 和 A'D',
则
∵△ABC ∽△A′B′C′
∴∠B =∠B' ,
∴△ABD ∽△A' B' D'
∴
探究新知
两边成比例且夹角相等的两个三角形相似
结论:相似三角形对应中线的比等于相似比
A
B
C
A'
B'
C'
D'
D
归纳总结
且都等于相似比.
A'
B'
A
B
C
D'
D
F
F'
E
E'
符号语言
相似三角形对应高的比,
对应角平分线的比
对应中线的比都相等,
∵△ABC∽△ A′B′C′ ,相似比是 k
且 AD、A′D′是对应边的高线,
BF、B′F′是对应边的中线,
CE、C′E′是对应角的角平分线,
∴
练一练
B
练一练
B
探究新知
【探究二】相似三角形的周长有什么关系呢?
解:如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB = kA'B',BC = kB'C',CA = kC'A',
从而
A
B
C
A'
B'
C'
结论:相似三角形周长的比等于相似比
探究新知
【探究三】相似三角形面积的比与相似比有什么关系?
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
探究新知
A
B
A'
B'
D'
D
C'
C
由前面的结论,得
结论:相似三角形面积的比等于相似比的平方
作三角形的高
例题练习
如图,在 △ABC 和 △DEF 中,AB = 2DE ,AC = 2DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
A
B
C
D
E
F
例题练习
A
B
C
D
E
F
解:在 △ABC 和 △DEF 中,∵ AB = 2DE,AC = 2DF,
又 ∵∠D =∠A,
∴ △DEF ∽ △ABC ,相似比为
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
∴
两边成比例且夹角相等的两个三角形相似
B
A
D
C
A
D
12
3
小结
相似三角形的性质:
1.相似三角形对应高的比,对应中线的比、对应角平分线的比都等于相似比.
2.相似三角形周长的比等于相似比.
3.相似三角形面积的比等于相似比的平方
谢谢同学们的聆听
