2024-2025学年初中数学人教版九年级下册 27.3位似(课时2) 课件(共33张PPT)
文档属性
| 名称 | 2024-2025学年初中数学人教版九年级下册 27.3位似(课时2) 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:13:33 | ||
图片预览








文档简介
(共33张PPT)
27.3位似
(课时2)
第二十七章 相似
素养目标
1.理解平面直角坐标系中,位似图形对应点的坐标之
间的联系;
2.会用图形的坐标的变化表示图形的位似变换,掌握把一个图形按一定比例放大或缩小后,点的坐标变化的规律;
重难点
知识回顾
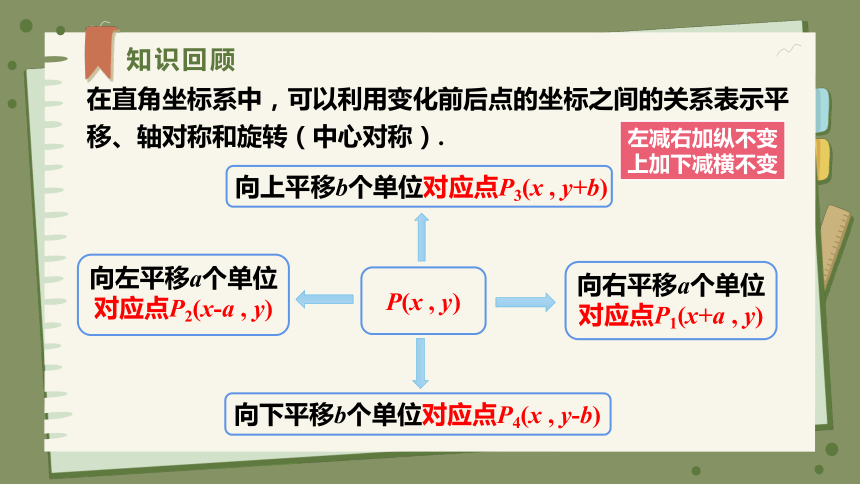
在直角坐标系中,可以利用变化前后点的坐标之间的关系表示平移、轴对称和旋转(中心对称).
向左平移a个单位
对应点P2(x-a , y)
向右平移a个单位
对应点P1(x+a , y)
向上平移b个单位对应点P3(x , y+b)
向下平移b个单位对应点P4(x , y-b)
P(x , y)
左减右加纵不变
上加下减横不变
知识回顾
A(x,-y)
P(x,y)
关于x轴对称
在平面坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.
A(-x,y)
P(x,y)
关于y轴对称
在平面坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数.
在直角坐标系中,可以利用变化前后点的坐标之间的关系表示平移、轴对称和旋转(中心对称).
知识回顾
P′(-x,-y)
P(x,y)
关于原点对称
在平面坐标系中,关于原点对称的点的横、纵坐标都互为相反数.
在直角坐标系中,可以利用变化前后点的坐标之间的关系表示平移、轴对称和旋转(中心对称).
新知导入
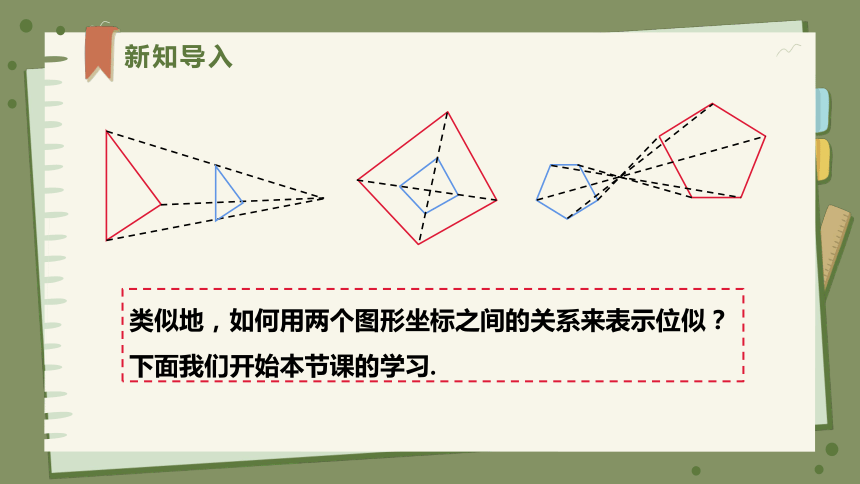
类似地,如何用两个图形坐标之间的关系来表示位似?
下面我们开始本节课的学习.
探究新知
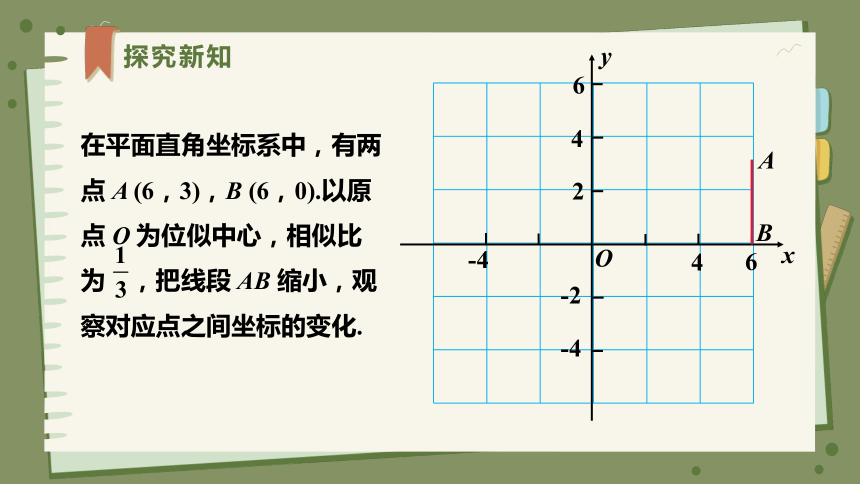
在平面直角坐标系中,有两点 A (6,3),B (6,0).以原点 O 为位似中心,相似比为 ,把线段 AB 缩小,观察对应点之间坐标的变化.
2
4
6
4
6
-2
-4
-4
x
y
A
B
O
探究新知
2
4
6
4
6
B'
-2
-4
-4
x
y
B
A'
A"
B"
O
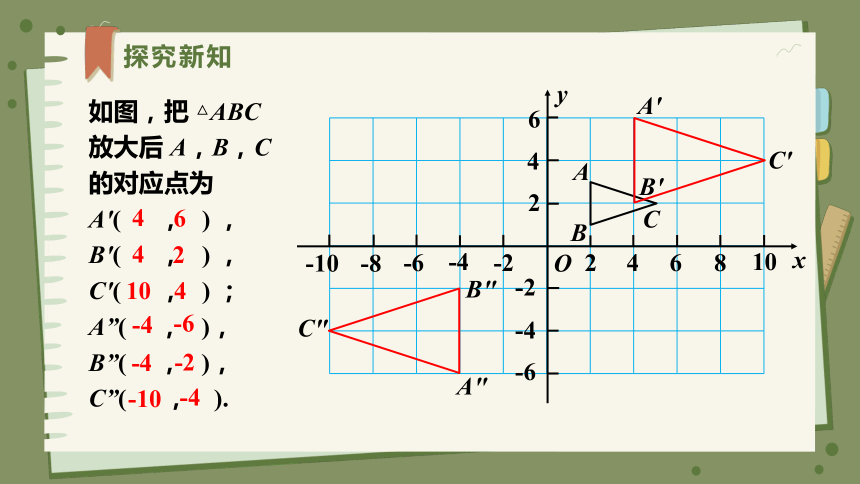
如图,把 AB 缩小后 A,B 的对应点为
A′ ( , ),
B' ( , ),
A" ( , ),
B" ( , ).
2
1
2
0
-2
-1
-2
0
探究新知
如图,△ABC 三个顶点坐标分别为 A (2,3),B (2,1),C (5,2),以点 O 为位似中心,相似比为 2,将 △ABC 放大,观察对应顶点坐标的变化.
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-6
O
探究新知
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-6
B'
A'
C'
A"
B"
C"
如图,把 △ABC 放大后 A,B,C 的对应点为
A'( , ) ,
B'( , ) ,
C'( , ) ;
A”( , ),
B”( , ),C”( , ).
4
6
4
2
10
4
-4
-6
-4
-2
-10
-4
O
探究新知
思考1:在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
思考2:所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
两个
当位似图形在原点同侧时,其对应顶点的坐标的比为 k;当位似图形在原点两侧时,其对应顶点的坐标的比为 -k.
归纳总结
一般地,在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
【注意】上面的坐标的变化规律是以原点为位似中心的位似变化中图形上对应点的坐标的变化规律.
当 k>1 时,图形扩大为原来的 k 倍;
当 0<k<1时,图形缩小为原来的 k 倍.
例题练习
如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 3 : 2.
2
4
6
2
-2
-4
x
y
A
B
O
例题练习
2
4
6
2
-2
-4
x
y
A
B
O
【分析】画三角形关键是确定它各顶点的坐标. 根据前面的归纳可知,点 A 的对应点 A′ 的坐标为
即(-3,6),类似地,可以确定其他顶点的坐标.
例题练习
2
4
6
2
-2
-4
x
y
A
B
O
A′
B′
解:利用位似中对应点的坐标的变化规律,分别取点 A′ (-3,6),B′ (-3,0),O (0,0).顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
归纳总结
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,总结它们的坐标变化规律
①平移变换:对应点的横坐标或纵坐标加上(或减去)平移的单位长度
②轴对称变换:以x轴为对称轴则对应点的横坐标相等,纵坐标互为相反数;以y轴为对称轴则对应点的纵坐标相等,横坐标互为相反数.
③旋转变换:一个图形绕原点旋转180°,则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数.
④位似变换:当以原点为位似中心时,变换前后两个图形对应点的横、纵坐标之比的绝对值等于位似比.
归纳总结
位似与平移、轴对称、旋转三种变换的联系和区别
位似、平移、轴对称、旋转都是图形变换的基本形式,它们的本质区别在于:平移、轴对称、旋转三种图形变换都是全等变换,而位似变换是相似(扩大、缩小或不变)变换.
A
D
D
C
C
D
B
小结
在原点同侧 : P'(kx,ky)
图形变换
平移
中心对称
对称
左右平移 m后 : P'(x±m,y)
上下平移 n后 : P'(x,y±n)
P'(-x,-y)
位似
P(x,y)
关于 x 轴 : P'(-x,y)
在原点异侧 : P'(-kx,-ky)
关于 y 轴 : P'(x,-y)
谢谢同学们的聆听
27.3位似
(课时2)
第二十七章 相似
素养目标
1.理解平面直角坐标系中,位似图形对应点的坐标之
间的联系;
2.会用图形的坐标的变化表示图形的位似变换,掌握把一个图形按一定比例放大或缩小后,点的坐标变化的规律;
重难点
知识回顾
在直角坐标系中,可以利用变化前后点的坐标之间的关系表示平移、轴对称和旋转(中心对称).
向左平移a个单位
对应点P2(x-a , y)
向右平移a个单位
对应点P1(x+a , y)
向上平移b个单位对应点P3(x , y+b)
向下平移b个单位对应点P4(x , y-b)
P(x , y)
左减右加纵不变
上加下减横不变
知识回顾
A(x,-y)
P(x,y)
关于x轴对称
在平面坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.
A(-x,y)
P(x,y)
关于y轴对称
在平面坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数.
在直角坐标系中,可以利用变化前后点的坐标之间的关系表示平移、轴对称和旋转(中心对称).
知识回顾
P′(-x,-y)
P(x,y)
关于原点对称
在平面坐标系中,关于原点对称的点的横、纵坐标都互为相反数.
在直角坐标系中,可以利用变化前后点的坐标之间的关系表示平移、轴对称和旋转(中心对称).
新知导入
类似地,如何用两个图形坐标之间的关系来表示位似?
下面我们开始本节课的学习.
探究新知
在平面直角坐标系中,有两点 A (6,3),B (6,0).以原点 O 为位似中心,相似比为 ,把线段 AB 缩小,观察对应点之间坐标的变化.
2
4
6
4
6
-2
-4
-4
x
y
A
B
O
探究新知
2
4
6
4
6
B'
-2
-4
-4
x
y
B
A'
A"
B"
O
如图,把 AB 缩小后 A,B 的对应点为
A′ ( , ),
B' ( , ),
A" ( , ),
B" ( , ).
2
1
2
0
-2
-1
-2
0
探究新知
如图,△ABC 三个顶点坐标分别为 A (2,3),B (2,1),C (5,2),以点 O 为位似中心,相似比为 2,将 △ABC 放大,观察对应顶点坐标的变化.
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-6
O
探究新知
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-6
B'
A'
C'
A"
B"
C"
如图,把 △ABC 放大后 A,B,C 的对应点为
A'( , ) ,
B'( , ) ,
C'( , ) ;
A”( , ),
B”( , ),C”( , ).
4
6
4
2
10
4
-4
-6
-4
-2
-10
-4
O
探究新知
思考1:在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
思考2:所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
两个
当位似图形在原点同侧时,其对应顶点的坐标的比为 k;当位似图形在原点两侧时,其对应顶点的坐标的比为 -k.
归纳总结
一般地,在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
【注意】上面的坐标的变化规律是以原点为位似中心的位似变化中图形上对应点的坐标的变化规律.
当 k>1 时,图形扩大为原来的 k 倍;
当 0<k<1时,图形缩小为原来的 k 倍.
例题练习
如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 3 : 2.
2
4
6
2
-2
-4
x
y
A
B
O
例题练习
2
4
6
2
-2
-4
x
y
A
B
O
【分析】画三角形关键是确定它各顶点的坐标. 根据前面的归纳可知,点 A 的对应点 A′ 的坐标为
即(-3,6),类似地,可以确定其他顶点的坐标.
例题练习
2
4
6
2
-2
-4
x
y
A
B
O
A′
B′
解:利用位似中对应点的坐标的变化规律,分别取点 A′ (-3,6),B′ (-3,0),O (0,0).顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
归纳总结
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,总结它们的坐标变化规律
①平移变换:对应点的横坐标或纵坐标加上(或减去)平移的单位长度
②轴对称变换:以x轴为对称轴则对应点的横坐标相等,纵坐标互为相反数;以y轴为对称轴则对应点的纵坐标相等,横坐标互为相反数.
③旋转变换:一个图形绕原点旋转180°,则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数.
④位似变换:当以原点为位似中心时,变换前后两个图形对应点的横、纵坐标之比的绝对值等于位似比.
归纳总结
位似与平移、轴对称、旋转三种变换的联系和区别
位似、平移、轴对称、旋转都是图形变换的基本形式,它们的本质区别在于:平移、轴对称、旋转三种图形变换都是全等变换,而位似变换是相似(扩大、缩小或不变)变换.
A
D
D
C
C
D
B
小结
在原点同侧 : P'(kx,ky)
图形变换
平移
中心对称
对称
左右平移 m后 : P'(x±m,y)
上下平移 n后 : P'(x,y±n)
P'(-x,-y)
位似
P(x,y)
关于 x 轴 : P'(-x,y)
在原点异侧 : P'(-kx,-ky)
关于 y 轴 : P'(x,-y)
谢谢同学们的聆听
