2024-2025学年初中数学人教版九年级下册 28.1锐角三角函数(课时1) 课件(共33张PPT)
文档属性
| 名称 | 2024-2025学年初中数学人教版九年级下册 28.1锐角三角函数(课时1) 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 19.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:14:01 | ||
图片预览





文档简介
(共33张PPT)
28.1锐角三角函数
(课时1)
第二十八章 锐角三角函数
素养目标
1.理解并掌握锐角正弦的定义,知道当直角三角形的锐角固定时,它的对边与斜边的比值都固定 (即正弦值不变);
2.能根据正弦概念正确进行计算;
3.培养学生良好的数形结合的能力,激发学生的求知欲和学习的自信心.
重点
重难点
情境导入
意大利比萨斜塔
意大利比萨斜塔在1350年落成时就已倾斜,其塔顶中点偏离垂直中心线2.1m.1972年比萨地区发生地震,这座高54.5m的斜塔在大幅度摇摆后仍巍然屹立,但塔顶中心点偏离垂直中心线增至5.2m,而且还以每年增加1cm的速度继续倾斜,随时都有倒塌的危险.为此,意大利当局从1990年起对斜塔维修纠偏,2001年竣工,此时塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8cm.
情境导入
意大利比萨斜塔
【提问】根据上述信息,你能用“塔身中心线与垂直中心线所成的角 ”来描述比萨斜塔的倾斜程度吗?
θ
垂直中心线
塔身中心线
探究新知
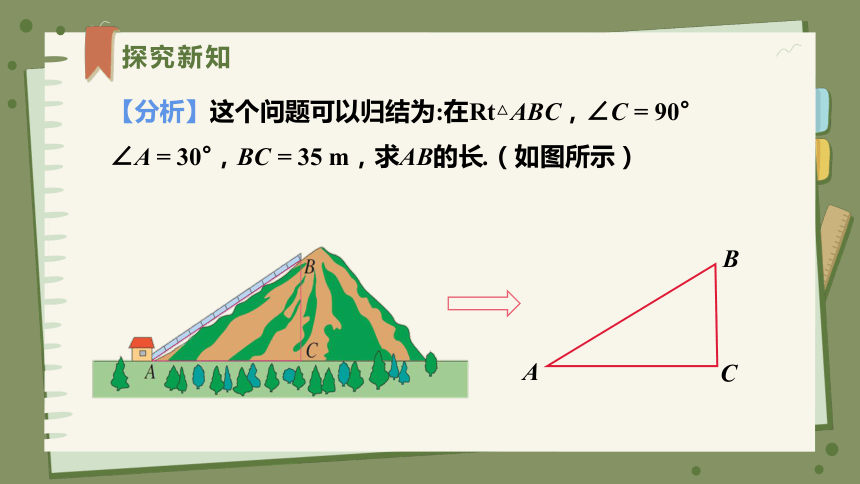
【探究一】为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡的坡角(∠A)为30°,为使出水口的高度为35m,需要准备多长的水管?
探究新知
【分析】这个问题可以归结为:在Rt△ABC,∠C = 90°
∠A = 30°,BC = 35 m,求AB的长.(如图所示)
A
C
B
探究新知
A
C
B
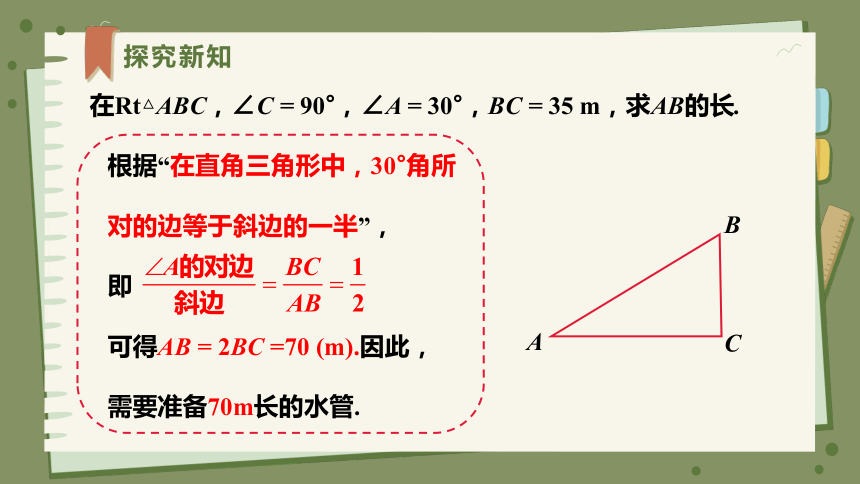
在Rt△ABC,∠C = 90°,∠A = 30°,BC = 35 m,求AB的长.
根据“在直角三角形中,30°角所对的边等于斜边的一半”,
即
可得AB = 2BC =70 (m).因此,需要准备70m长的水管.
探究新知
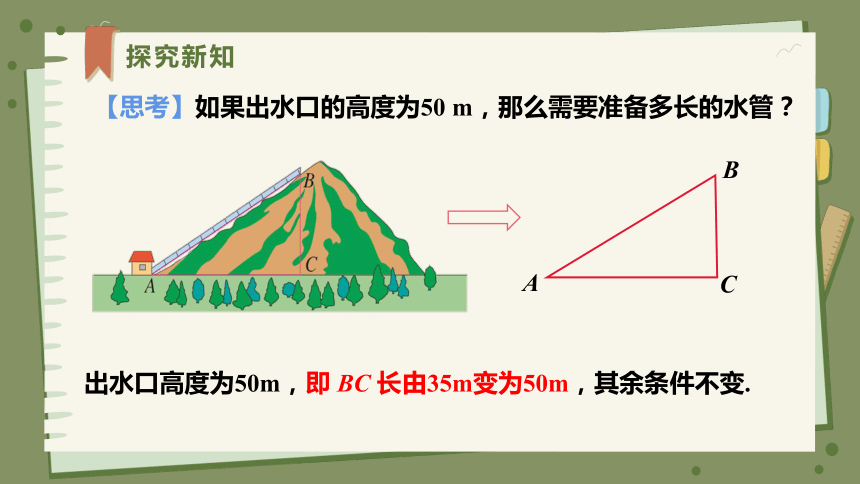
【思考】如果出水口的高度为50 m,那么需要准备多长的水管?
A
C
B
出水口高度为50m,即 BC 长由35m变为50m,其余条件不变.
探究新知
A
C
B
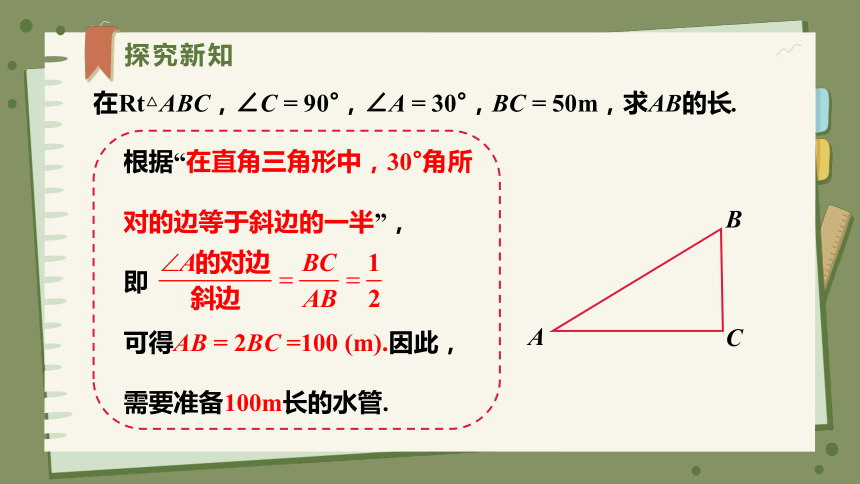
在Rt△ABC,∠C = 90°,∠A = 30°,BC = 50m,求AB的长.
根据“在直角三角形中,30°角所对的边等于斜边的一半”,
即
可得AB = 2BC =100 (m).因此,需要准备100m长的水管.
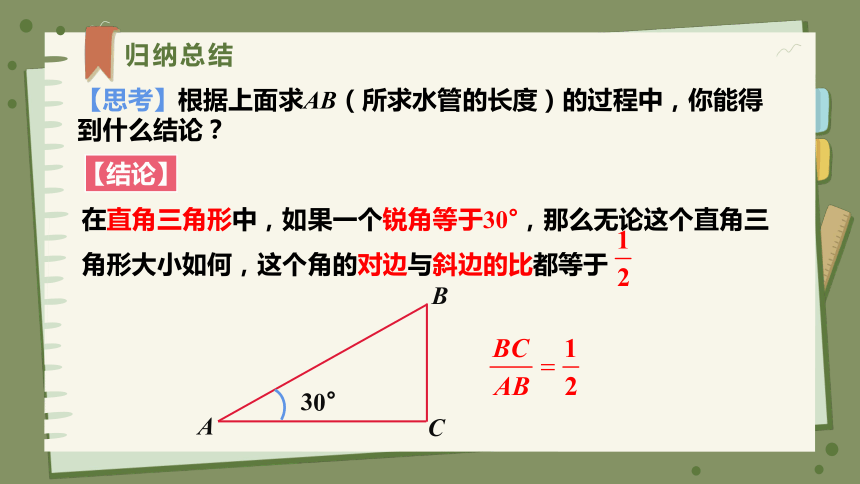
归纳总结
【思考】根据上面求AB(所求水管的长度)的过程中,你能得到什么结论?
【结论】
在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
A
B
C
30°
探究新知
A
C
B
45°
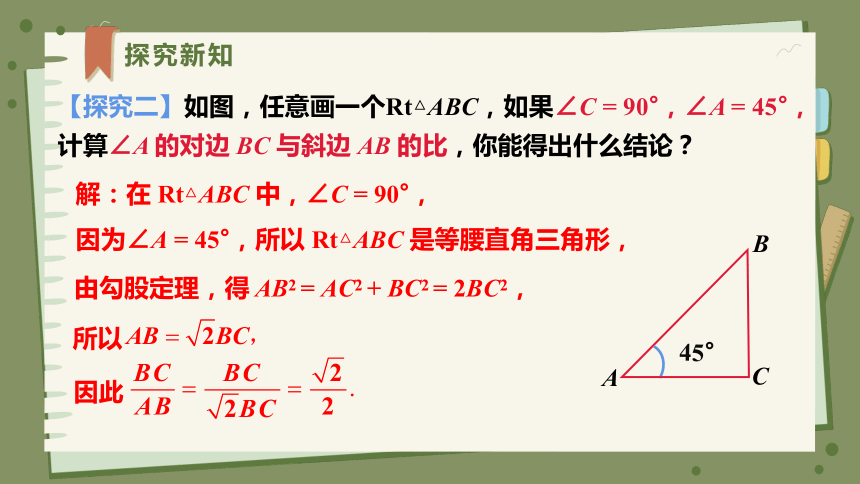
【探究二】如图,任意画一个Rt△ABC,如果∠C = 90°,∠A = 45°,计算∠A 的对边 BC 与斜边 AB 的比,你能得出什么结论?
解:在 Rt△ABC 中,∠C = 90°,
因为∠A = 45°,所以 Rt△ABC 是等腰直角三角形,
由勾股定理,得 AB2 = AC2 + BC2 = 2BC2,
所以
因此
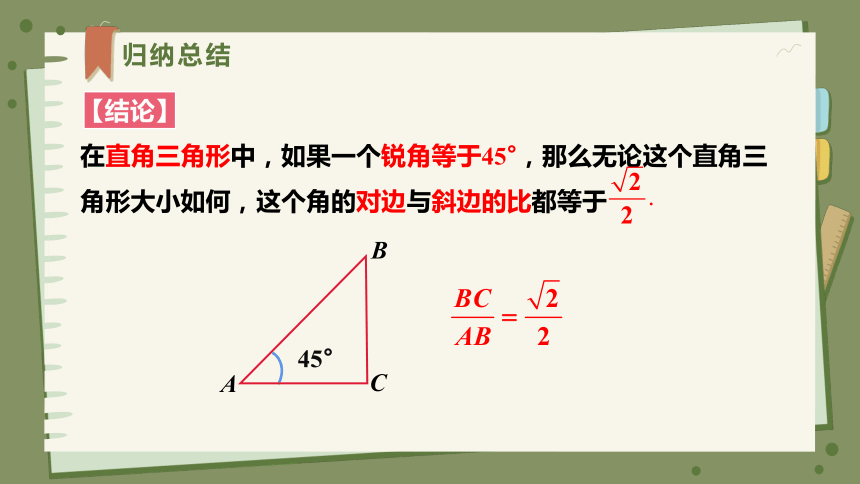
归纳总结
【结论】
在直角三角形中,如果一个锐角等于45°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
A
C
B
45°
探究新知
【探究三】在 Rt△ABC 中,如果 ∠C = 90°,∠A = a, 那么 ∠A 的对边 BC 与斜边 AB 的比是一个定值吗?
A
B
C
a
探究新知
任意画 Rt△ABC 和 Rt△ A'B'C' ,使得 ∠C =∠C' = 90°,
∠A =∠A' = α,那么 与 有什么关系?
a
A
B
C
a
A'
B'
C'
探究新知
A
B
C
a
因为∠C=∠C'=90°,∠A=∠A'=α,
所以 Rt△ABC ∽Rt△A'B'C'.
所以
【结论】在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的对边与斜边的比都是一个固定值.
a
A'
B'
C'
归纳总结
【结论】如图,在Rt△ABC中,∠C = 90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sin A.
例如,当∠A = 30°时,我们有
当∠A = 45°时,我们有
A
B
C
邻边b
对边a
斜边c
归纳总结
(1)“sinA”是一个完整的符号,单独写符号 sin 是没有意义的,表达时有时要省去角的符号“∠”
sin∠DEF、 sin∠1 (不能省去角的符号)
sinA 、 sin39 °、 sinβ (省去角的符号)
注意
(2)对于锐角A 的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是∠A的函数.
(3)∠A的正弦sinA随着∠A的变化而变化
例题练习
如图,在 Rt△ABC 中,∠C = 90°,求 sinA 和sinB 的值.
A
B
C
4
3
图1
?
A
B
C
13
5
图2
?
例题练习
解:如图1,在 Rt△ABC 中,由勾股定理得
因此
如图2,在Rt△ABC中,由勾股定理得
因此
A
B
C
13
5
图2
?
A
B
C
4
3
图1
?
A
C
D
D
A
小结
A
B
C
a
锐角
三角函数
两边比值一定
正弦
1.在直角三角形中
2.对应边的比值
3.建立等式(方程思想)
角度变化,比值变化
谢谢同学们的聆听
28.1锐角三角函数
(课时1)
第二十八章 锐角三角函数
素养目标
1.理解并掌握锐角正弦的定义,知道当直角三角形的锐角固定时,它的对边与斜边的比值都固定 (即正弦值不变);
2.能根据正弦概念正确进行计算;
3.培养学生良好的数形结合的能力,激发学生的求知欲和学习的自信心.
重点
重难点
情境导入
意大利比萨斜塔
意大利比萨斜塔在1350年落成时就已倾斜,其塔顶中点偏离垂直中心线2.1m.1972年比萨地区发生地震,这座高54.5m的斜塔在大幅度摇摆后仍巍然屹立,但塔顶中心点偏离垂直中心线增至5.2m,而且还以每年增加1cm的速度继续倾斜,随时都有倒塌的危险.为此,意大利当局从1990年起对斜塔维修纠偏,2001年竣工,此时塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8cm.
情境导入
意大利比萨斜塔
【提问】根据上述信息,你能用“塔身中心线与垂直中心线所成的角 ”来描述比萨斜塔的倾斜程度吗?
θ
垂直中心线
塔身中心线
探究新知
【探究一】为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡的坡角(∠A)为30°,为使出水口的高度为35m,需要准备多长的水管?
探究新知
【分析】这个问题可以归结为:在Rt△ABC,∠C = 90°
∠A = 30°,BC = 35 m,求AB的长.(如图所示)
A
C
B
探究新知
A
C
B
在Rt△ABC,∠C = 90°,∠A = 30°,BC = 35 m,求AB的长.
根据“在直角三角形中,30°角所对的边等于斜边的一半”,
即
可得AB = 2BC =70 (m).因此,需要准备70m长的水管.
探究新知
【思考】如果出水口的高度为50 m,那么需要准备多长的水管?
A
C
B
出水口高度为50m,即 BC 长由35m变为50m,其余条件不变.
探究新知
A
C
B
在Rt△ABC,∠C = 90°,∠A = 30°,BC = 50m,求AB的长.
根据“在直角三角形中,30°角所对的边等于斜边的一半”,
即
可得AB = 2BC =100 (m).因此,需要准备100m长的水管.
归纳总结
【思考】根据上面求AB(所求水管的长度)的过程中,你能得到什么结论?
【结论】
在直角三角形中,如果一个锐角等于30°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
A
B
C
30°
探究新知
A
C
B
45°
【探究二】如图,任意画一个Rt△ABC,如果∠C = 90°,∠A = 45°,计算∠A 的对边 BC 与斜边 AB 的比,你能得出什么结论?
解:在 Rt△ABC 中,∠C = 90°,
因为∠A = 45°,所以 Rt△ABC 是等腰直角三角形,
由勾股定理,得 AB2 = AC2 + BC2 = 2BC2,
所以
因此
归纳总结
【结论】
在直角三角形中,如果一个锐角等于45°,那么无论这个直角三角形大小如何,这个角的对边与斜边的比都等于
A
C
B
45°
探究新知
【探究三】在 Rt△ABC 中,如果 ∠C = 90°,∠A = a, 那么 ∠A 的对边 BC 与斜边 AB 的比是一个定值吗?
A
B
C
a
探究新知
任意画 Rt△ABC 和 Rt△ A'B'C' ,使得 ∠C =∠C' = 90°,
∠A =∠A' = α,那么 与 有什么关系?
a
A
B
C
a
A'
B'
C'
探究新知
A
B
C
a
因为∠C=∠C'=90°,∠A=∠A'=α,
所以 Rt△ABC ∽Rt△A'B'C'.
所以
【结论】在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的对边与斜边的比都是一个固定值.
a
A'
B'
C'
归纳总结
【结论】如图,在Rt△ABC中,∠C = 90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sin A.
例如,当∠A = 30°时,我们有
当∠A = 45°时,我们有
A
B
C
邻边b
对边a
斜边c
归纳总结
(1)“sinA”是一个完整的符号,单独写符号 sin 是没有意义的,表达时有时要省去角的符号“∠”
sin∠DEF、 sin∠1 (不能省去角的符号)
sinA 、 sin39 °、 sinβ (省去角的符号)
注意
(2)对于锐角A 的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是∠A的函数.
(3)∠A的正弦sinA随着∠A的变化而变化
例题练习
如图,在 Rt△ABC 中,∠C = 90°,求 sinA 和sinB 的值.
A
B
C
4
3
图1
?
A
B
C
13
5
图2
?
例题练习
解:如图1,在 Rt△ABC 中,由勾股定理得
因此
如图2,在Rt△ABC中,由勾股定理得
因此
A
B
C
13
5
图2
?
A
B
C
4
3
图1
?
A
C
D
D
A
小结
A
B
C
a
锐角
三角函数
两边比值一定
正弦
1.在直角三角形中
2.对应边的比值
3.建立等式(方程思想)
角度变化,比值变化
谢谢同学们的聆听
