2024-2025学年初中数学人教版九年级下册 28.1锐角三角函数(课时3) 课件(共32张PPT)
文档属性
| 名称 | 2024-2025学年初中数学人教版九年级下册 28.1锐角三角函数(课时3) 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 19.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:16:35 | ||
图片预览








文档简介
(共32张PPT)
28.1锐角三角函数
(课时3)
第二十八章 锐角三角函数
素养目标
1.运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数值;
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用;
3. 学会利用计算器求非特殊角的三角函数值、会根据三角
函数值求锐角度数并进行相关计算.
重点
重难点
知识回顾
A
B
C
邻边b
对边a
斜边c
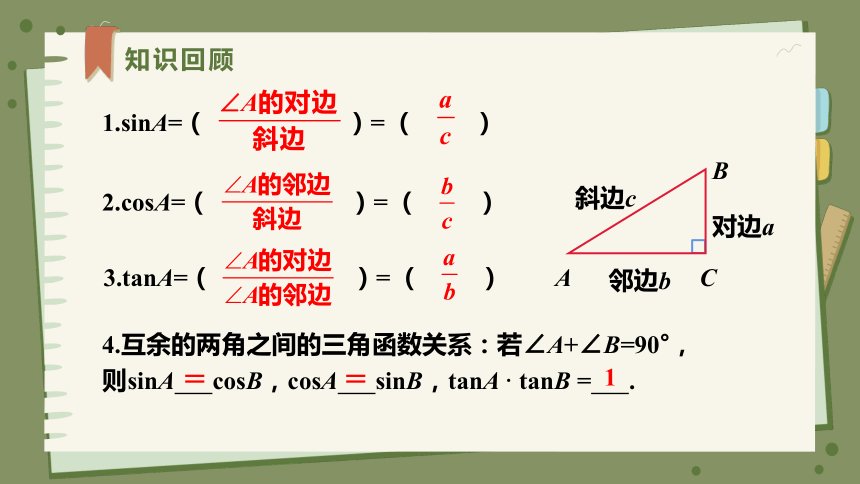
1.sinA=( )= ( )
2.cosA=( )= ( )
3.tanA=( )= ( )
4.互余的两角之间的三角函数关系:若∠A+∠B=90°,则sinA cosB,cosA sinB,tanA · tanB = .
=
=
1
新知导入
我们在推导正弦关系的时候得到了两个特殊角的正弦值
1. sin30°= ( )
2.sin45°= ( )
新知导入
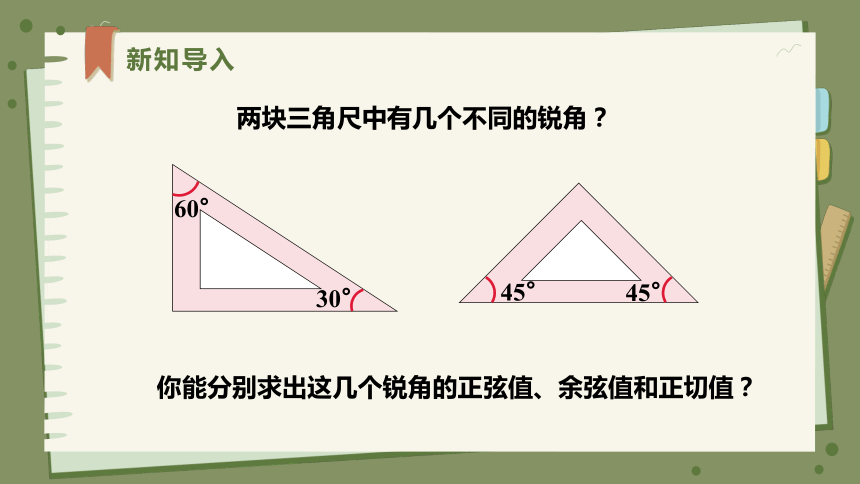
两块三角尺中有几个不同的锐角?
30°
60°
45°
45°
你能分别求出这几个锐角的正弦值、余弦值和正切值?
探究新知
30°
60°
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
勾股定理
∴
探究新知
30°
60°
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
勾股定理
∴
探究新知
45°
45°
设两条直角边长为 a,则斜边长 =
勾股定理
∴
归纳总结
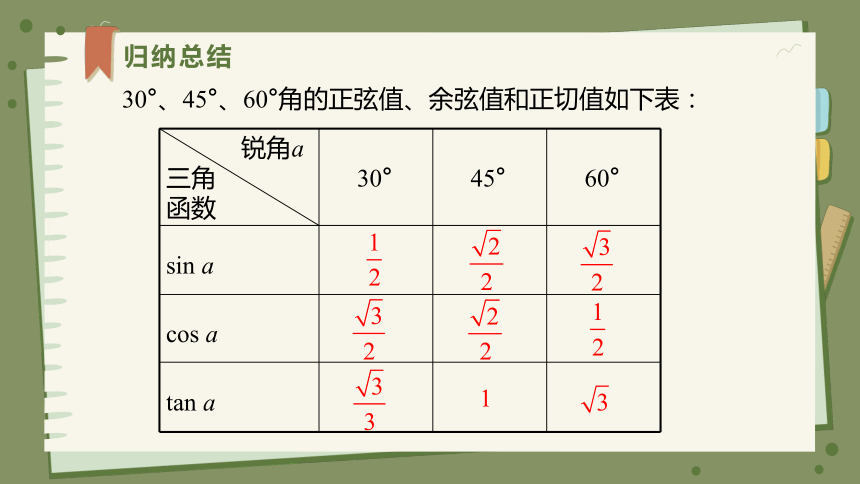
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a 三角 函数 30° 45° 60°
sin a
cos a
tan a
1
例题练习
求下列各式的值:
(1)cos260°+ sin260° (2)
解:(1)cos260°+sin260°
解:(2)
cos260°表示(cos60°)2,
即(cos60°)×(cos60°).
例题练习
如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
A
B
C
解: 在图中,
∴ ∠A = 45°.
∵
例题练习
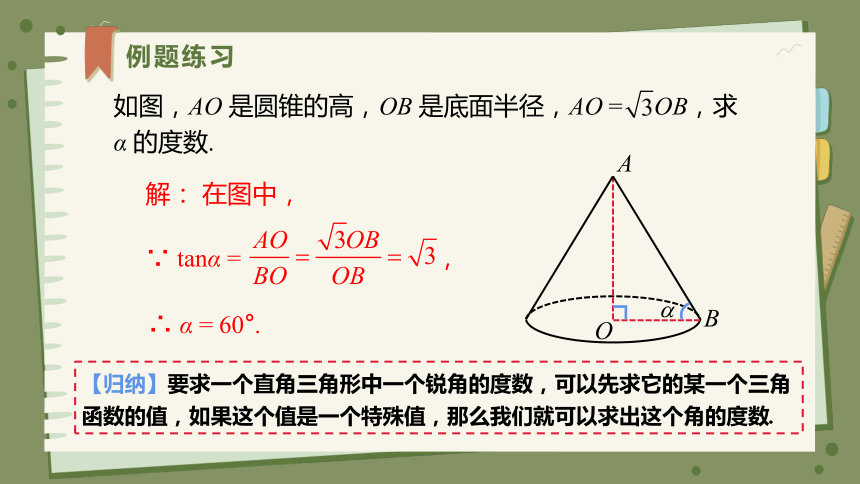
如图,AO 是圆锥的高,OB 是底面半径,AO = OB,求 α 的度数.
解: 在图中,
∴ α = 60°.
∵ tanα = ,
A
B
O
【归纳】要求一个直角三角形中一个锐角的度数,可以先求它的某一个三角函数的值,如果这个值是一个特殊值,那么我们就可以求出这个角的度数.
探究新知
【思考】通过前面的学习,我们知道当锐角 A 是 30°、45°、60°等特殊角时,可以求得这些特殊角的锐角三角函数值;如果锐角 A 不是这些特殊角,怎样得到它的锐角三角函数值呢?
借助计算器进行计算
探究新知
利用计算器求三角函数值、角的度数
(1)用计算器求sin18°的值;
(2)用计算器求tan30°36′的值;
(3)已知sinA=0.5018,用计算器求锐角∠A的度数.
探究新知
(1)用计算器求sin18°的值;
解:第一步:按计算器 键;
sin
第二步:输入角度值18;
屏幕显示结果 sin18°= 0.309 016 994.
不同计算器操作的步骤可能不同!
探究新知
(2)用计算器求 tan30°36′ 的值;
解:方法①:
第二步:输入角度值30.6 (因为30°36′ = 30.6°);
屏幕显示答案:0.591 398 351.
第一步:按计算器 键;
tan
探究新知
(2)用计算器求 tan30°36′ 的值;
解:方法②:
屏幕显示答案:0.591 398 351.
第一步:按计算器 键;
tan
第二步:输入角度值30,分值36 (使用 键);
D.M′S
探究新知
(3)已知 sinA = 0.501 8,用计算器求 ∠A 的度数.
第二步:然后输入函数值0. 5018;
屏幕显示答案: 30.119 158 67°(按实际需要进行精确).
解:
第一步:按计算器 键;
2nd F
sin
还可以利用 键,
进一步得到∠A = 30°07′08.97 ″
这说明锐角 A 精确到 1′ 的结果为 30°7′,
精确到 1″ 的结果为30°7′9″.
2nd F
D.M′S
B
A
B
75°
小结
锐角a 三角 函数 30° 45° 60°
sin a
cos a
tan a
1
谢谢同学们的聆听
28.1锐角三角函数
(课时3)
第二十八章 锐角三角函数
素养目标
1.运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数值;
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用;
3. 学会利用计算器求非特殊角的三角函数值、会根据三角
函数值求锐角度数并进行相关计算.
重点
重难点
知识回顾
A
B
C
邻边b
对边a
斜边c
1.sinA=( )= ( )
2.cosA=( )= ( )
3.tanA=( )= ( )
4.互余的两角之间的三角函数关系:若∠A+∠B=90°,则sinA cosB,cosA sinB,tanA · tanB = .
=
=
1
新知导入
我们在推导正弦关系的时候得到了两个特殊角的正弦值
1. sin30°= ( )
2.sin45°= ( )
新知导入
两块三角尺中有几个不同的锐角?
30°
60°
45°
45°
你能分别求出这几个锐角的正弦值、余弦值和正切值?
探究新知
30°
60°
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
勾股定理
∴
探究新知
30°
60°
设30°所对的直角边长为a,那么斜边长为2a,
另一条直角边长 =
勾股定理
∴
探究新知
45°
45°
设两条直角边长为 a,则斜边长 =
勾股定理
∴
归纳总结
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a 三角 函数 30° 45° 60°
sin a
cos a
tan a
1
例题练习
求下列各式的值:
(1)cos260°+ sin260° (2)
解:(1)cos260°+sin260°
解:(2)
cos260°表示(cos60°)2,
即(cos60°)×(cos60°).
例题练习
如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
A
B
C
解: 在图中,
∴ ∠A = 45°.
∵
例题练习
如图,AO 是圆锥的高,OB 是底面半径,AO = OB,求 α 的度数.
解: 在图中,
∴ α = 60°.
∵ tanα = ,
A
B
O
【归纳】要求一个直角三角形中一个锐角的度数,可以先求它的某一个三角函数的值,如果这个值是一个特殊值,那么我们就可以求出这个角的度数.
探究新知
【思考】通过前面的学习,我们知道当锐角 A 是 30°、45°、60°等特殊角时,可以求得这些特殊角的锐角三角函数值;如果锐角 A 不是这些特殊角,怎样得到它的锐角三角函数值呢?
借助计算器进行计算
探究新知
利用计算器求三角函数值、角的度数
(1)用计算器求sin18°的值;
(2)用计算器求tan30°36′的值;
(3)已知sinA=0.5018,用计算器求锐角∠A的度数.
探究新知
(1)用计算器求sin18°的值;
解:第一步:按计算器 键;
sin
第二步:输入角度值18;
屏幕显示结果 sin18°= 0.309 016 994.
不同计算器操作的步骤可能不同!
探究新知
(2)用计算器求 tan30°36′ 的值;
解:方法①:
第二步:输入角度值30.6 (因为30°36′ = 30.6°);
屏幕显示答案:0.591 398 351.
第一步:按计算器 键;
tan
探究新知
(2)用计算器求 tan30°36′ 的值;
解:方法②:
屏幕显示答案:0.591 398 351.
第一步:按计算器 键;
tan
第二步:输入角度值30,分值36 (使用 键);
D.M′S
探究新知
(3)已知 sinA = 0.501 8,用计算器求 ∠A 的度数.
第二步:然后输入函数值0. 5018;
屏幕显示答案: 30.119 158 67°(按实际需要进行精确).
解:
第一步:按计算器 键;
2nd F
sin
还可以利用 键,
进一步得到∠A = 30°07′08.97 ″
这说明锐角 A 精确到 1′ 的结果为 30°7′,
精确到 1″ 的结果为30°7′9″.
2nd F
D.M′S
B
A
B
75°
小结
锐角a 三角 函数 30° 45° 60°
sin a
cos a
tan a
1
谢谢同学们的聆听
