第十八章 平行四边形 综合素质评价(含答案)人教版数学八年级下册
文档属性
| 名称 | 第十八章 平行四边形 综合素质评价(含答案)人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 301.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:46:44 | ||
图片预览



文档简介
第十八章综合素质评价
时间:90分钟 满分:120分
一、选择题(每题3分,共30分)
1.在中,若 ,则的度数为( )
A. B. C. D.
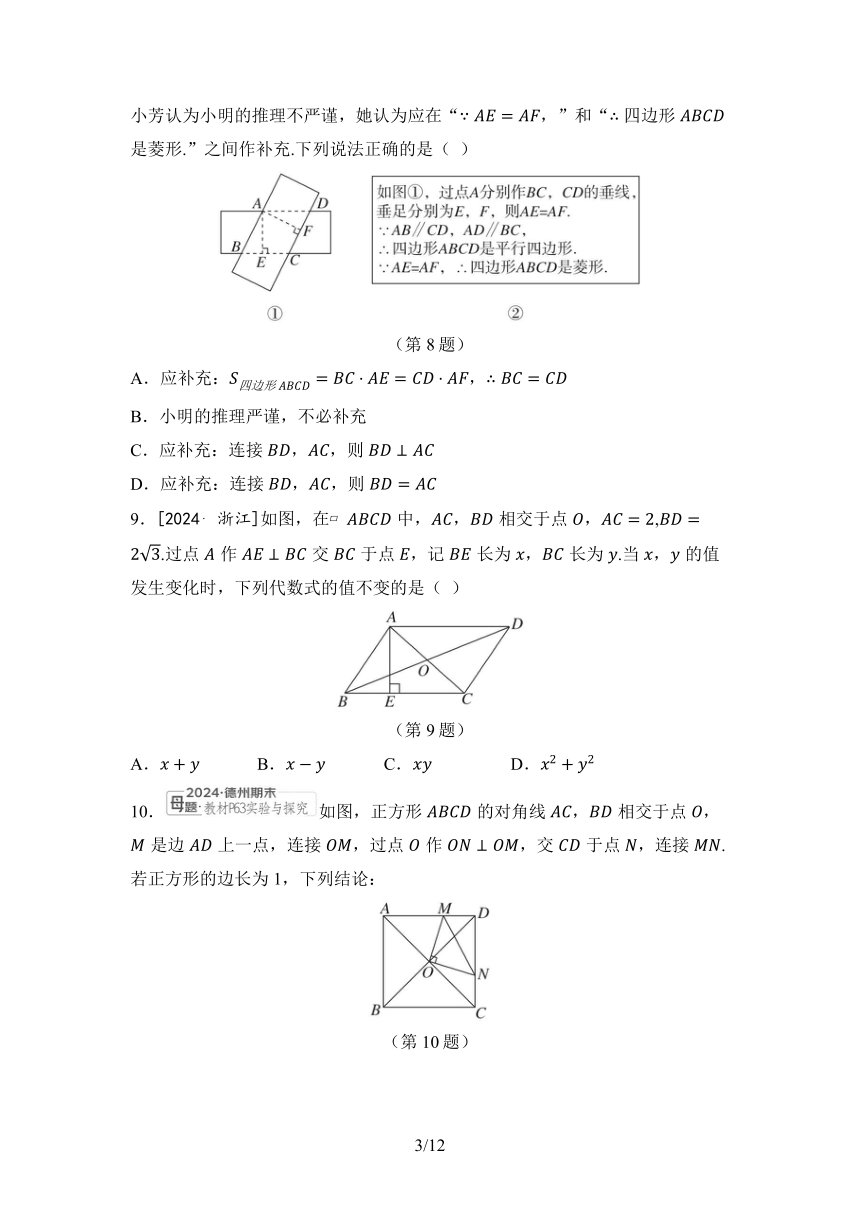
2.[2024 武汉黄陂区期中]如图,在中,,,则边的长不可能是( )
(第2题)
A.3 B.5 C.8 D.10
3.[2024 江门期末]如图为汽车常备的一种千斤顶的原理图,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变的大小(菱形的边长不变).当 时,的度数为( )
(第3题)
A. B. C. D.
4.如图,在矩形中,对角线与相交于点,,分别是,的中点,且,则的长度为( )
(第4题)
A.2 B.4 C.6 D.8
5.如图,一根竹竿斜靠在竖直的墙上,是的中点,表示竹竿沿墙上下移动过程中的某个位置,在竹竿移动过程中( )
(第5题)
A.下移时,点,之间的距离增大
B.上移时,点,之间的距离减小
C.只要移动,点,之间的距离就变化
D.无论怎样移动,点,之间的距离不变
6.如图,四边形 为平行四边形,延长 到点,使,连接,,.下列条件中,不能使四边形 成为矩形的是( )
(第6题)
A. B.
C. D.
7.[2024 石家庄新华区一模]小明用四根长度相等的木条制作了能够活动的菱形学具,他先活动学具成为图①所示的菱形,并测得 ,接着活动学具成为图②所示的正方形,并测得对角线,则图①中菱形的对角线的长为( )
(第7题)
A.20 B.30 C. D.
8.如图①,将两张宽度相同的矩形纸条交叉叠放.小明发现重叠部分(四边形)是菱形,并进行了如图②推理:
小芳认为小明的推理不严谨,她认为应在“,”和“ 四边形是菱形.”之间作补充.下列说法正确的是( )
(第8题)
A.应补充:,
B.小明的推理严谨,不必补充
C.应补充:连接,,则
D.应补充:连接,,则
9.[2024 浙江]如图,在中,,相交于点,,.过点作交于点,记长为,长为.当,的值发生变化时,下列代数式的值不变的是( )
(第9题)
A. B. C. D.
10.如图,正方形的对角线,相交于点,是边上一点,连接,过点作,交于点,连接.若正方形的边长为1,下列结论:
(第10题)
;;;始终是等腰直角三角形.其中正确的为( )
A.①② B.①②③ C.①②④ D.①②③④
二、填空题(每题4分,共24分)
11.[2024 上海]在菱形中, ,则________.
12.已知菱形的对角线,相交于点,添加条件____________________________可使菱形成为正方形.
13.一个平行四边形的一条边长是3,两条对角线的长分别是4和,则此平行四边形的面积为________.
14.如图,矩形的顶点在轴上,点的坐标为.固定边,向左“推”矩形,使点落在轴的点的位置,则点的对应点的坐标为____________.
(第14题)
15.如图,在正方形 中,对角线 与 相交于点,为 上一点,,为 的中点,若 的周长为18,则 的长为________.
(第15题)
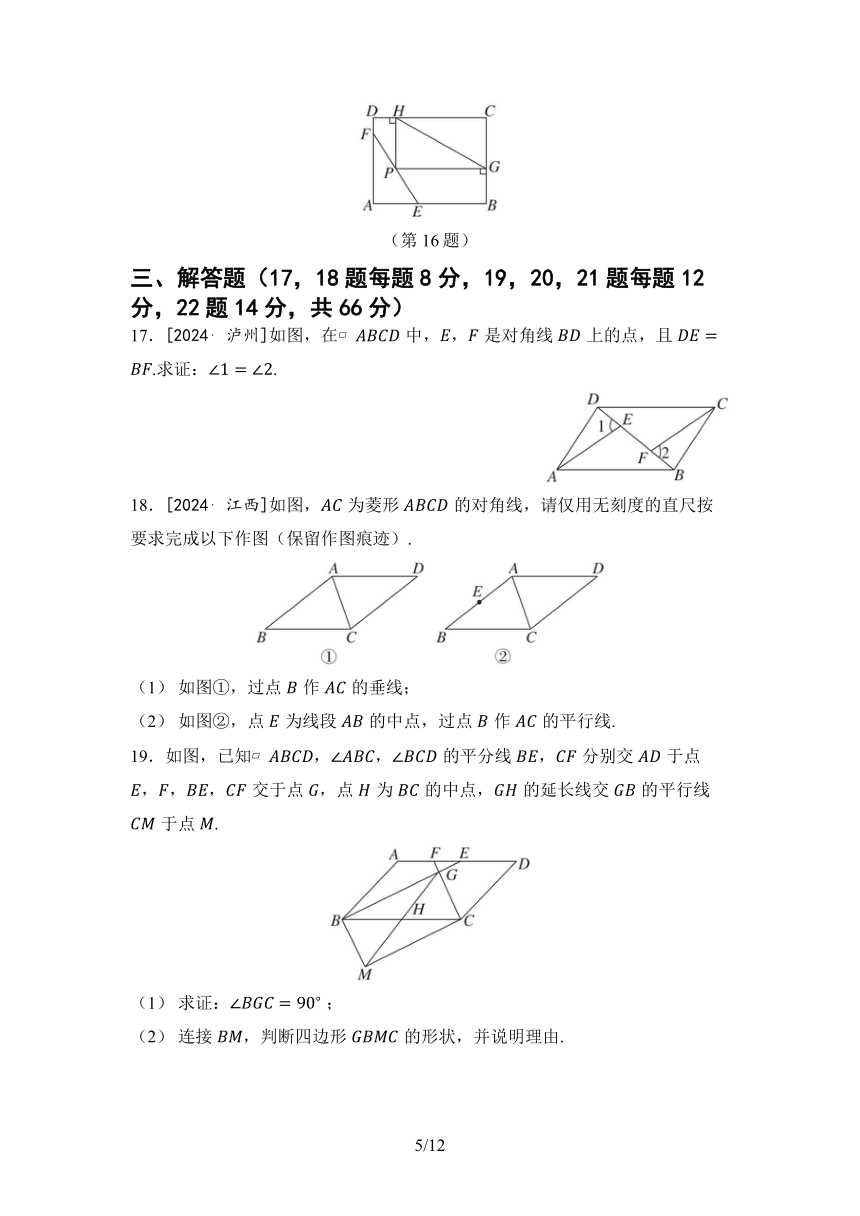
16.如图,在矩形 中,,分别是边,上的动点,是线段 的中点,,,垂足分别为,,连接.若,,,则 的最小值是______.
(第16题)
三、解答题(17,18题每题8分,19,20,21题每题12分,22题14分,共66分)
17.[2024 泸州]如图,在中,,是对角线上的点,且.求证:.
18.[2024 江西]如图,为菱形的对角线,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1) 如图①,过点作的垂线;
(2) 如图②,点为线段的中点,过点作的平行线.
19.如图,已知,,的平分线,分别交于点,,,交于点,点为的中点,的延长线交的平行线于点.
(1) 求证: ;
(2) 连接,判断四边形的形状,并说明理由.
20.荣荣从一副七巧板(如图①)中取出了其中的六块,拼成了一个(如图②),已知原来七巧板拼成正方形的边长为4.
(1) 图②中小正方形②的边长______,线段________;
(2) 求的对角线的长.
21.在矩形中,,,的垂直平分线分别交,于点,,垂足为.
(1) 如图①,连接,,试证明四边形为菱形,并求的长;
(2) 如图②,动点,分别从,两点同时出发,沿和的各边匀速运动一周后停止,点的运动路线为,点的运动路线为.在运动过程中,已知点的速度为,点的速度为,设运动时间为,当以,,,四点为顶点的四边形是平行四边形时,求的值.
22.如图①,把一个含 角的直角三角板和一个正方形摆放在一起,使三角板的直角顶点和正方形的顶点重合,点,分别在正方形的边,上,连接,取的中点和的中点,连接,.
(1) 连接,求证:;
(2) 在(1)的条件下,请判断线段与之间的数量关系,并证明;
(3) 如图②,将这个含 角的直角三角板的直角顶点和正方形的顶点重合,点,分别在正方形的边,的延长线上,其他条件不变,当,时,求的长.
【参考答案】
第十八章综合素质评价
八年级数学 下(版)时间:90分钟 满分:120分
一、选择题(每题3分,共30分)
1.B
2.D
3.A
4.A
5.D
6.B
7.C
8.A
9.C
[解析]点拨:过点D作,交的延长线于点,则 .
,.
四边形是平行四边形,,,
,,
,,
由勾股定理得,
,
,
,
,即,
当,的值发生变化时,代数式的值不变的是.
10.D
[解析]点拨:四边形是正方形,且正方形的边长为1,
,, , ,,.
, .
,
,,
,,,
,是等腰直角三角形,,故①②④正确;
,,,
,,故③正确.
二、填空题(每题4分,共24分)
11.
12.(答案不唯一)
13.
14.
15.
[解析]点拨:四边形是正方形,, ,.
为的中点,.
的周长为18,.
又,,
,即.
,,
.
,,.
16.8
[解析]点拨:如图,连接,,,
四边形是矩形,
, ,
.
是的中点,.
,, ,
四边形是矩形,,
当,,三点共线时,的长最小,为,的最小值是8.
三、解答题(17,18题每题8分,19,20,21题每题12分,22题14分,共66分)
17.证明: 四边形是平行四边形,
,,,
又,,
.
18.(1) 解:如图①,即为所求.
(2) 如图②,即为所求.(画法不唯一)
19.(1) 证明: 四边形是平行四边形,
.
,分别平分,,
,,
,
.
(2) 解:四边形是矩形,理由如下:
点为的中点, ,
,.
,,,
,,
四边形为矩形.
20.(1) ;
(2) 解:延长,过点作于点,如图,
根据七巧板的特点可知,为等腰直角三角形,
, .
,为等腰直角三角形,
由勾股定理可得,
,
.
21.(1) 解: 四边形是矩形,
, .
,.
垂直平分,垂足为,即,,
.
四边形为平行四边形.
又, 四边形为菱形..
设,则.
在中,,由勾股定理得,解得.
(2) 显然当点在上,点在上时,以,,,四点为顶点不可能构成平行四边形;同理,当点在上,点在或上时,也不可能构成平行四边形.
只有当点在上,点在上时,才能构成平行四边形.
如图,连接,.
若以,,,四点为顶点的四边形是平行四边形,则.
,点的速度为,点的速度为,运动时间为,
,.
,解得.
当以,,,四点为顶点的四边形是平行四边形时,.
22.(1) 证明: 四边形是正方形,
, .
是等腰直角三角形,,
,即,
,.
(2) 解:.
证明:是的中点,是的中点,
是的中位线,,
在中,是的中点,,
,.
(3) 解:连接,
四边形是正方形,.
,,,
在中,由勾股定理得.
是的中点,是的中点,
是的中位线,.
/
时间:90分钟 满分:120分
一、选择题(每题3分,共30分)
1.在中,若 ,则的度数为( )
A. B. C. D.
2.[2024 武汉黄陂区期中]如图,在中,,,则边的长不可能是( )
(第2题)
A.3 B.5 C.8 D.10
3.[2024 江门期末]如图为汽车常备的一种千斤顶的原理图,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变的大小(菱形的边长不变).当 时,的度数为( )
(第3题)
A. B. C. D.
4.如图,在矩形中,对角线与相交于点,,分别是,的中点,且,则的长度为( )
(第4题)
A.2 B.4 C.6 D.8
5.如图,一根竹竿斜靠在竖直的墙上,是的中点,表示竹竿沿墙上下移动过程中的某个位置,在竹竿移动过程中( )
(第5题)
A.下移时,点,之间的距离增大
B.上移时,点,之间的距离减小
C.只要移动,点,之间的距离就变化
D.无论怎样移动,点,之间的距离不变
6.如图,四边形 为平行四边形,延长 到点,使,连接,,.下列条件中,不能使四边形 成为矩形的是( )
(第6题)
A. B.
C. D.
7.[2024 石家庄新华区一模]小明用四根长度相等的木条制作了能够活动的菱形学具,他先活动学具成为图①所示的菱形,并测得 ,接着活动学具成为图②所示的正方形,并测得对角线,则图①中菱形的对角线的长为( )
(第7题)
A.20 B.30 C. D.
8.如图①,将两张宽度相同的矩形纸条交叉叠放.小明发现重叠部分(四边形)是菱形,并进行了如图②推理:
小芳认为小明的推理不严谨,她认为应在“,”和“ 四边形是菱形.”之间作补充.下列说法正确的是( )
(第8题)
A.应补充:,
B.小明的推理严谨,不必补充
C.应补充:连接,,则
D.应补充:连接,,则
9.[2024 浙江]如图,在中,,相交于点,,.过点作交于点,记长为,长为.当,的值发生变化时,下列代数式的值不变的是( )
(第9题)
A. B. C. D.
10.如图,正方形的对角线,相交于点,是边上一点,连接,过点作,交于点,连接.若正方形的边长为1,下列结论:
(第10题)
;;;始终是等腰直角三角形.其中正确的为( )
A.①② B.①②③ C.①②④ D.①②③④
二、填空题(每题4分,共24分)
11.[2024 上海]在菱形中, ,则________.
12.已知菱形的对角线,相交于点,添加条件____________________________可使菱形成为正方形.
13.一个平行四边形的一条边长是3,两条对角线的长分别是4和,则此平行四边形的面积为________.
14.如图,矩形的顶点在轴上,点的坐标为.固定边,向左“推”矩形,使点落在轴的点的位置,则点的对应点的坐标为____________.
(第14题)
15.如图,在正方形 中,对角线 与 相交于点,为 上一点,,为 的中点,若 的周长为18,则 的长为________.
(第15题)
16.如图,在矩形 中,,分别是边,上的动点,是线段 的中点,,,垂足分别为,,连接.若,,,则 的最小值是______.
(第16题)
三、解答题(17,18题每题8分,19,20,21题每题12分,22题14分,共66分)
17.[2024 泸州]如图,在中,,是对角线上的点,且.求证:.
18.[2024 江西]如图,为菱形的对角线,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1) 如图①,过点作的垂线;
(2) 如图②,点为线段的中点,过点作的平行线.
19.如图,已知,,的平分线,分别交于点,,,交于点,点为的中点,的延长线交的平行线于点.
(1) 求证: ;
(2) 连接,判断四边形的形状,并说明理由.
20.荣荣从一副七巧板(如图①)中取出了其中的六块,拼成了一个(如图②),已知原来七巧板拼成正方形的边长为4.
(1) 图②中小正方形②的边长______,线段________;
(2) 求的对角线的长.
21.在矩形中,,,的垂直平分线分别交,于点,,垂足为.
(1) 如图①,连接,,试证明四边形为菱形,并求的长;
(2) 如图②,动点,分别从,两点同时出发,沿和的各边匀速运动一周后停止,点的运动路线为,点的运动路线为.在运动过程中,已知点的速度为,点的速度为,设运动时间为,当以,,,四点为顶点的四边形是平行四边形时,求的值.
22.如图①,把一个含 角的直角三角板和一个正方形摆放在一起,使三角板的直角顶点和正方形的顶点重合,点,分别在正方形的边,上,连接,取的中点和的中点,连接,.
(1) 连接,求证:;
(2) 在(1)的条件下,请判断线段与之间的数量关系,并证明;
(3) 如图②,将这个含 角的直角三角板的直角顶点和正方形的顶点重合,点,分别在正方形的边,的延长线上,其他条件不变,当,时,求的长.
【参考答案】
第十八章综合素质评价
八年级数学 下(版)时间:90分钟 满分:120分
一、选择题(每题3分,共30分)
1.B
2.D
3.A
4.A
5.D
6.B
7.C
8.A
9.C
[解析]点拨:过点D作,交的延长线于点,则 .
,.
四边形是平行四边形,,,
,,
,,
由勾股定理得,
,
,
,
,即,
当,的值发生变化时,代数式的值不变的是.
10.D
[解析]点拨:四边形是正方形,且正方形的边长为1,
,, , ,,.
, .
,
,,
,,,
,是等腰直角三角形,,故①②④正确;
,,,
,,故③正确.
二、填空题(每题4分,共24分)
11.
12.(答案不唯一)
13.
14.
15.
[解析]点拨:四边形是正方形,, ,.
为的中点,.
的周长为18,.
又,,
,即.
,,
.
,,.
16.8
[解析]点拨:如图,连接,,,
四边形是矩形,
, ,
.
是的中点,.
,, ,
四边形是矩形,,
当,,三点共线时,的长最小,为,的最小值是8.
三、解答题(17,18题每题8分,19,20,21题每题12分,22题14分,共66分)
17.证明: 四边形是平行四边形,
,,,
又,,
.
18.(1) 解:如图①,即为所求.
(2) 如图②,即为所求.(画法不唯一)
19.(1) 证明: 四边形是平行四边形,
.
,分别平分,,
,,
,
.
(2) 解:四边形是矩形,理由如下:
点为的中点, ,
,.
,,,
,,
四边形为矩形.
20.(1) ;
(2) 解:延长,过点作于点,如图,
根据七巧板的特点可知,为等腰直角三角形,
, .
,为等腰直角三角形,
由勾股定理可得,
,
.
21.(1) 解: 四边形是矩形,
, .
,.
垂直平分,垂足为,即,,
.
四边形为平行四边形.
又, 四边形为菱形..
设,则.
在中,,由勾股定理得,解得.
(2) 显然当点在上,点在上时,以,,,四点为顶点不可能构成平行四边形;同理,当点在上,点在或上时,也不可能构成平行四边形.
只有当点在上,点在上时,才能构成平行四边形.
如图,连接,.
若以,,,四点为顶点的四边形是平行四边形,则.
,点的速度为,点的速度为,运动时间为,
,.
,解得.
当以,,,四点为顶点的四边形是平行四边形时,.
22.(1) 证明: 四边形是正方形,
, .
是等腰直角三角形,,
,即,
,.
(2) 解:.
证明:是的中点,是的中点,
是的中位线,,
在中,是的中点,,
,.
(3) 解:连接,
四边形是正方形,.
,,,
在中,由勾股定理得.
是的中点,是的中点,
是的中位线,.
/
