第十九章 一次函数 综合素质评价(含答案)人教版数学八年级下册
文档属性
| 名称 | 第十九章 一次函数 综合素质评价(含答案)人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 397.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 14:47:51 | ||
图片预览



文档简介
第十九章综合素质评价
八年级数学 下(版)时间:90分钟 满分:120分
一、选择题(每题3分,共30分)
1.[2024· 上海金山区期末]下列函数中是一次函数的是( )
A. B.
C. D.
2.已知正比例函数的图象经过点,则的值为( )
A. B. C. D.1
3.将直线沿轴向下平移7个单位长度后,得到的直线与轴的交点坐标是( )
A. B. C. D.
4.若点和都在直线上,则与的大小关系是( )
A. B. C. D.无法确定
5.有一张长为,宽为的矩形木板,现要将长减少,则剩余木板的面积与的关系式为(其中)( )
A. B. C. D.
6.已知直线与直线,为常数,且的交点的纵坐标为5,则关于,的二元一次方程组的解为( )
A. B. C. D.
7.一次函数与正比例函数,为常数,且在同一平面直角坐标系中的图象不可能是( )
A.
B.
C.
D.
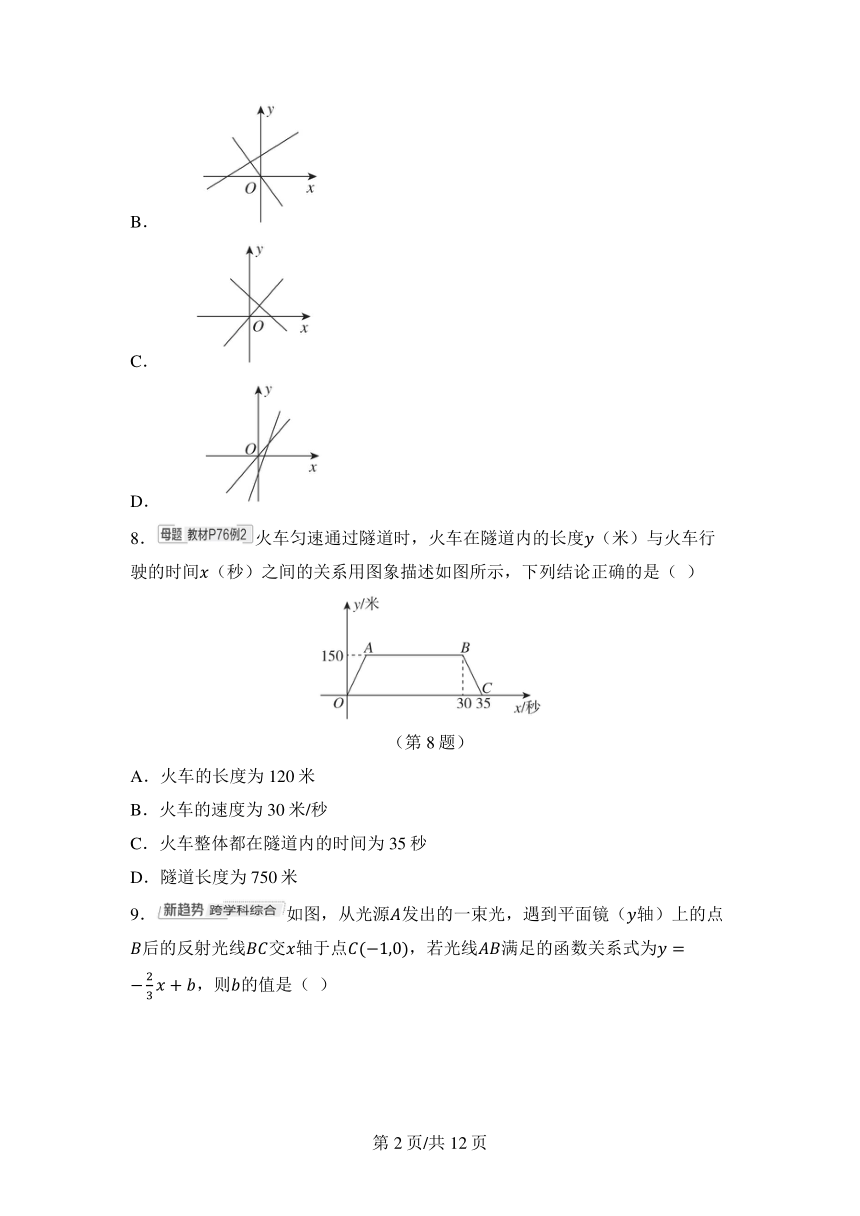
8.火车匀速通过隧道时,火车在隧道内的长度(米)与火车行驶的时间(秒)之间的关系用图象描述如图所示,下列结论正确的是( )
(第8题)
A.火车的长度为120米
B.火车的速度为30米/秒
C.火车整体都在隧道内的时间为35秒
D.隧道长度为750米
9.如图,从光源 发出的一束光,遇到平面镜(轴)上的点后的反射光线交轴于点,若光线满足的函数关系式为,则的值是( )
(第9题)
A.2 B. C. D.1
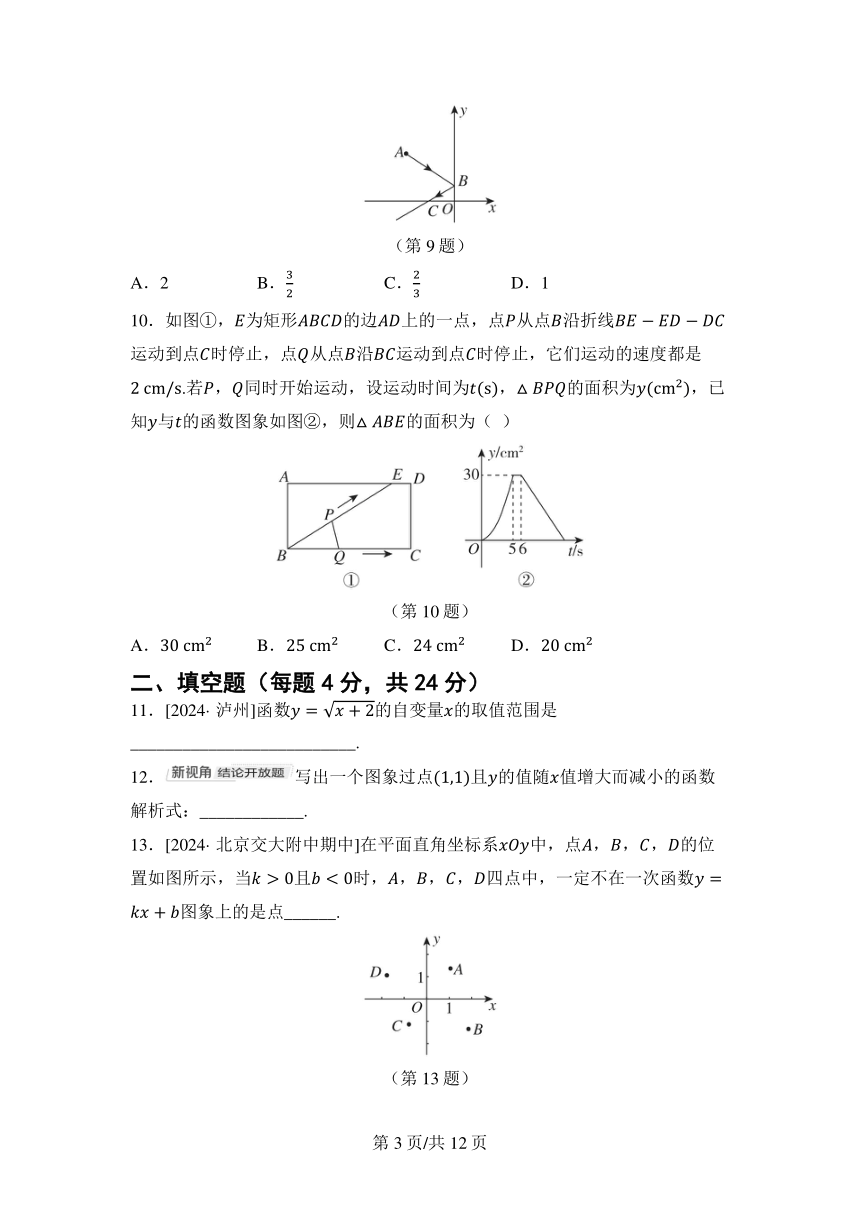
10.如图①,为矩形的边上的一点,点从点沿折线运动到点时停止,点从点沿运动到点时停止,它们运动的速度都是.若,同时开始运动,设运动时间为,的面积为,已知与的函数图象如图②,则的面积为( )
(第10题)
A. B. C. D.
二、填空题(每题4分,共24分)
11.[2024· 泸州]函数的自变量的取值范围是__________________________.
12.写出一个图象过点且的值随值增大而减小的函数解析式:____________.
13.[2024· 北京交大附中期中]在平面直角坐标系中,点,,,的位置如图所示,当且时,,,,四点中,一定不在一次函数图象上的是点______.
(第13题)
14.甲无人机从地面起飞,乙无人机从距离地面高的楼顶起飞,两架无人机同时匀速上升,所在的位置距离地面的高度(单位:)与无人机上升的时间(单位:)之间的关系如图所示,则上升时两架无人机的高度相差__.
(第14题)
15.如图,正方形 和正方形 分别有一条边在 轴的正半轴上,顶点,在直线 上,如果正方形 的边长是1,那么点 的坐标是______________.
(第15题)
16.如图,直线 与直线 相交于点,直线 与 轴交于点,直线 与 轴交于点,与 轴交于点,过点 作 交 轴于点.直线 上有一点(在 轴上方)且,则点的坐标为____________.
(第16题)
三、解答题(17,18题每题8分,19,20,21题每题12分,22题14分,共66分)
17.地壳的厚度约为,在地表以下不太深的地方,温度可按计算,其中是深度,是地表温度,是所达深度处地壳的温度.
(1) 在这个变化过程中,自变量和因变量分别是什么?
(2) 如果地表温度为,那么深度为时地壳的温度是多少?
18.[2024· 北京朝阳区期末]如图,在平面直角坐标系中,函数与的图象交于点.
(1) 若点的横坐标为2,求的值;
(2) 若关于的不等式有且只有2个正整数解,直接写出的取值范围.
19.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量(千瓦时)关于已行驶路程(千米)的函数图象.
(1) 根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程.当时,求消耗1千瓦时的电量汽车能行驶的路程;
(2) 当时,求关于的函数解析式,并计算当汽车已行驶186千米时,蓄电池的剩余电量.
20.某地地震发生后,根据救灾指挥中心的信息,甲、乙两个重灾区急需一种大型挖掘机,甲地需要27台,乙地需要25台,,两省获知情况后慷慨相助,分别捐赠该型号挖掘机28台和24台,并将其全部调往灾区,如果从省调运一台挖掘机到甲地耗资0.4万元,到乙地耗资0.3万元;从省调运一台挖掘机到甲地耗资0.5万元,到乙地耗资0.2万元.设从省调往甲地台挖掘机,,两省将捐赠的挖掘机全部调往灾区共耗资万元.
(1) 用含的代数式填写下表.
运往甲地(单位:台) 运往乙地(单位:台)
省 ______________________________________________
省 __________ ________
(2) 求与之间的函数关系式,并直接写出自变量的取值范围.
(3) 若总耗资不超过16.2万元,共有几种调运方案?哪种调运方案的总耗资最少?
21.综合与实践:生活中的数学——古代计时器“漏壶”.
【问题情境】某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,该漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.
【实验观察】下表是实验记录的圆柱容器液面高度与时间的数据.
时间 1 2 3 4 5
圆柱容器液面高度 6 10 14 18 22
根据上述的实践活动,解决以下问题:
(1) 【探索发现】请你根据表中的数据在图②中描点、连线,并确定与之间的函数解析式;
(2) 【结论应用】如果本次实验记录的开始时间是上午,那么当圆柱容器液面高度达到时是几点?
22.如图,在平面直角坐标系中,直线交轴于点,交轴于点,点的坐标为,直线与直线相交于点,点的横坐标为1.
(1) 求直线的解析式.
(2) 若点是轴上一点,且的面积是面积的,求点的坐标.
(3) 在轴右侧是否存在一点,使得以点,,,为顶点的四边形是平行四边形?若存在,直接写出符合条件的点的坐标;若不存在,请说明理由.
【参考答案】
第十九章综合素质评价
八年级数学 下(版)时间:90分钟 满分:120分
一、选择题(每题3分,共30分)
1.D
2.C
3.B
4.B
5.C
6.A
7.A
8.B
[解析]点拨:由题图知线段表示火车正在进入隧道,点A表示火车刚好全部进入隧道,
火车的长度为150米,故A错误;
由题图知线段表示火车正在驶出隧道,点B表示火车驶出隧道的初始时刻,点C表示火车刚好完全驶出隧道,段所用时间为(秒),
火车的速度为(米/秒),故B正确;
段所用时间为(秒),
段所用时间为(秒),
火车整体都在隧道内的时间为25秒,故C错误;
(米), 隧道的长度为900米,故D错误.
9.C
[解析]点拨:如图,延长交轴于点D,
由反射角等于入射角得,
,
又,
,
,
.
,,,.
将点的坐标代入,
得,解得.
10.C
[解析]点拨:由题中图象可知,
,
,
连接,当时,,
,
.
二、填空题(每题4分,共24分)
11.(答案不唯一)
12.
13.D
14.20
15.
16.
[解析]点拨:是直线与轴的交点,,分别是直线与轴、轴的交点,
易得,,,.
联立 解得
点的坐标为,.
, 可设直线的解析式为.
易得, 直线的解析式为.
是直线与轴的交点,
易得点的坐标为.
,解得.
又 点在直线上,, 点的坐标为.
三、解答题(17,18题每题8分,19,20,21题每题12分,22题14分,共66分)
17.(1) 解:自变量是深度,因变量是所达深度处地壳的温度.
(2) 当,时,.
所以深度为时地壳的温度是.
18.(1) 解:对于,当时,,,
把点的坐标代入,得,解得.
(2) 的取值范围为.
19.(1) 解:由图象可知蓄电池剩余电量为35千瓦时时,汽车已行驶了150千米.
当时,消耗1千瓦时的电量汽车能行驶的路程为(千米).
(2) 设,
把点,的坐标分别代入,
得解得
,
当时,,
当时,关于的函数解析式为,当汽车已行驶186千米时,蓄电池的剩余电量为17千瓦时.
20.(1) (先从上到下,再从左到右填写); ;
(2) 解:由题意得,
即(且为整数).
(3) 依题意,得,解得.
,且为整数,或27.
则要使总耗资不超过16.2万元,共有两种调运方案:
方案一:从省往甲地调运26台,往乙地调运2台;从省往甲地调运1台,往乙地调运23台.
总耗资为(万元);
方案二:从省往甲地调运27台,往乙地调运1台;从省往甲地调运0台,往乙地调运24台.
总耗资为(万元).
, 调运方案二的总耗资最少.
21.(1) 解:如图.
由图象可知该函数是一次函数,设该函数的解析式为.
点,在该函数图象上,
解得
与之间的函数解析式为.
(2) 当时,,解得.
.
当圆柱容器液面高度达到时是上午10:30.
22.(1) 解:对于,当时,,
点的坐标为.
设直线的解析式为,
将点,的坐标分别代入,
得解得
直线的解析式为.
(2) 对于,当时,,
点的坐标为,.
,
,
, 点的坐标为或.
(3) 存在.点的坐标为或.
[解析]点拨:设点的坐标为,
如图,当为对角线时,四边形为平行四边形.
,,,
解得
点的坐标为;
当为对角线时,四边形为平行四边形.
,,,
解得
点的坐标为(不合题意,舍去);
当为对角线时,四边形是平行四边形.
,,,
解得
点的坐标为.
综上所述,在轴右侧存在一点,使得以点,,,为顶点的四边形是平行四边形,点的坐标为或.
第页/共页
八年级数学 下(版)时间:90分钟 满分:120分
一、选择题(每题3分,共30分)
1.[2024· 上海金山区期末]下列函数中是一次函数的是( )
A. B.
C. D.
2.已知正比例函数的图象经过点,则的值为( )
A. B. C. D.1
3.将直线沿轴向下平移7个单位长度后,得到的直线与轴的交点坐标是( )
A. B. C. D.
4.若点和都在直线上,则与的大小关系是( )
A. B. C. D.无法确定
5.有一张长为,宽为的矩形木板,现要将长减少,则剩余木板的面积与的关系式为(其中)( )
A. B. C. D.
6.已知直线与直线,为常数,且的交点的纵坐标为5,则关于,的二元一次方程组的解为( )
A. B. C. D.
7.一次函数与正比例函数,为常数,且在同一平面直角坐标系中的图象不可能是( )
A.
B.
C.
D.
8.火车匀速通过隧道时,火车在隧道内的长度(米)与火车行驶的时间(秒)之间的关系用图象描述如图所示,下列结论正确的是( )
(第8题)
A.火车的长度为120米
B.火车的速度为30米/秒
C.火车整体都在隧道内的时间为35秒
D.隧道长度为750米
9.如图,从光源 发出的一束光,遇到平面镜(轴)上的点后的反射光线交轴于点,若光线满足的函数关系式为,则的值是( )
(第9题)
A.2 B. C. D.1
10.如图①,为矩形的边上的一点,点从点沿折线运动到点时停止,点从点沿运动到点时停止,它们运动的速度都是.若,同时开始运动,设运动时间为,的面积为,已知与的函数图象如图②,则的面积为( )
(第10题)
A. B. C. D.
二、填空题(每题4分,共24分)
11.[2024· 泸州]函数的自变量的取值范围是__________________________.
12.写出一个图象过点且的值随值增大而减小的函数解析式:____________.
13.[2024· 北京交大附中期中]在平面直角坐标系中,点,,,的位置如图所示,当且时,,,,四点中,一定不在一次函数图象上的是点______.
(第13题)
14.甲无人机从地面起飞,乙无人机从距离地面高的楼顶起飞,两架无人机同时匀速上升,所在的位置距离地面的高度(单位:)与无人机上升的时间(单位:)之间的关系如图所示,则上升时两架无人机的高度相差__.
(第14题)
15.如图,正方形 和正方形 分别有一条边在 轴的正半轴上,顶点,在直线 上,如果正方形 的边长是1,那么点 的坐标是______________.
(第15题)
16.如图,直线 与直线 相交于点,直线 与 轴交于点,直线 与 轴交于点,与 轴交于点,过点 作 交 轴于点.直线 上有一点(在 轴上方)且,则点的坐标为____________.
(第16题)
三、解答题(17,18题每题8分,19,20,21题每题12分,22题14分,共66分)
17.地壳的厚度约为,在地表以下不太深的地方,温度可按计算,其中是深度,是地表温度,是所达深度处地壳的温度.
(1) 在这个变化过程中,自变量和因变量分别是什么?
(2) 如果地表温度为,那么深度为时地壳的温度是多少?
18.[2024· 北京朝阳区期末]如图,在平面直角坐标系中,函数与的图象交于点.
(1) 若点的横坐标为2,求的值;
(2) 若关于的不等式有且只有2个正整数解,直接写出的取值范围.
19.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量(千瓦时)关于已行驶路程(千米)的函数图象.
(1) 根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程.当时,求消耗1千瓦时的电量汽车能行驶的路程;
(2) 当时,求关于的函数解析式,并计算当汽车已行驶186千米时,蓄电池的剩余电量.
20.某地地震发生后,根据救灾指挥中心的信息,甲、乙两个重灾区急需一种大型挖掘机,甲地需要27台,乙地需要25台,,两省获知情况后慷慨相助,分别捐赠该型号挖掘机28台和24台,并将其全部调往灾区,如果从省调运一台挖掘机到甲地耗资0.4万元,到乙地耗资0.3万元;从省调运一台挖掘机到甲地耗资0.5万元,到乙地耗资0.2万元.设从省调往甲地台挖掘机,,两省将捐赠的挖掘机全部调往灾区共耗资万元.
(1) 用含的代数式填写下表.
运往甲地(单位:台) 运往乙地(单位:台)
省 ______________________________________________
省 __________ ________
(2) 求与之间的函数关系式,并直接写出自变量的取值范围.
(3) 若总耗资不超过16.2万元,共有几种调运方案?哪种调运方案的总耗资最少?
21.综合与实践:生活中的数学——古代计时器“漏壶”.
【问题情境】某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,该漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.
【实验观察】下表是实验记录的圆柱容器液面高度与时间的数据.
时间 1 2 3 4 5
圆柱容器液面高度 6 10 14 18 22
根据上述的实践活动,解决以下问题:
(1) 【探索发现】请你根据表中的数据在图②中描点、连线,并确定与之间的函数解析式;
(2) 【结论应用】如果本次实验记录的开始时间是上午,那么当圆柱容器液面高度达到时是几点?
22.如图,在平面直角坐标系中,直线交轴于点,交轴于点,点的坐标为,直线与直线相交于点,点的横坐标为1.
(1) 求直线的解析式.
(2) 若点是轴上一点,且的面积是面积的,求点的坐标.
(3) 在轴右侧是否存在一点,使得以点,,,为顶点的四边形是平行四边形?若存在,直接写出符合条件的点的坐标;若不存在,请说明理由.
【参考答案】
第十九章综合素质评价
八年级数学 下(版)时间:90分钟 满分:120分
一、选择题(每题3分,共30分)
1.D
2.C
3.B
4.B
5.C
6.A
7.A
8.B
[解析]点拨:由题图知线段表示火车正在进入隧道,点A表示火车刚好全部进入隧道,
火车的长度为150米,故A错误;
由题图知线段表示火车正在驶出隧道,点B表示火车驶出隧道的初始时刻,点C表示火车刚好完全驶出隧道,段所用时间为(秒),
火车的速度为(米/秒),故B正确;
段所用时间为(秒),
段所用时间为(秒),
火车整体都在隧道内的时间为25秒,故C错误;
(米), 隧道的长度为900米,故D错误.
9.C
[解析]点拨:如图,延长交轴于点D,
由反射角等于入射角得,
,
又,
,
,
.
,,,.
将点的坐标代入,
得,解得.
10.C
[解析]点拨:由题中图象可知,
,
,
连接,当时,,
,
.
二、填空题(每题4分,共24分)
11.(答案不唯一)
12.
13.D
14.20
15.
16.
[解析]点拨:是直线与轴的交点,,分别是直线与轴、轴的交点,
易得,,,.
联立 解得
点的坐标为,.
, 可设直线的解析式为.
易得, 直线的解析式为.
是直线与轴的交点,
易得点的坐标为.
,解得.
又 点在直线上,, 点的坐标为.
三、解答题(17,18题每题8分,19,20,21题每题12分,22题14分,共66分)
17.(1) 解:自变量是深度,因变量是所达深度处地壳的温度.
(2) 当,时,.
所以深度为时地壳的温度是.
18.(1) 解:对于,当时,,,
把点的坐标代入,得,解得.
(2) 的取值范围为.
19.(1) 解:由图象可知蓄电池剩余电量为35千瓦时时,汽车已行驶了150千米.
当时,消耗1千瓦时的电量汽车能行驶的路程为(千米).
(2) 设,
把点,的坐标分别代入,
得解得
,
当时,,
当时,关于的函数解析式为,当汽车已行驶186千米时,蓄电池的剩余电量为17千瓦时.
20.(1) (先从上到下,再从左到右填写); ;
(2) 解:由题意得,
即(且为整数).
(3) 依题意,得,解得.
,且为整数,或27.
则要使总耗资不超过16.2万元,共有两种调运方案:
方案一:从省往甲地调运26台,往乙地调运2台;从省往甲地调运1台,往乙地调运23台.
总耗资为(万元);
方案二:从省往甲地调运27台,往乙地调运1台;从省往甲地调运0台,往乙地调运24台.
总耗资为(万元).
, 调运方案二的总耗资最少.
21.(1) 解:如图.
由图象可知该函数是一次函数,设该函数的解析式为.
点,在该函数图象上,
解得
与之间的函数解析式为.
(2) 当时,,解得.
.
当圆柱容器液面高度达到时是上午10:30.
22.(1) 解:对于,当时,,
点的坐标为.
设直线的解析式为,
将点,的坐标分别代入,
得解得
直线的解析式为.
(2) 对于,当时,,
点的坐标为,.
,
,
, 点的坐标为或.
(3) 存在.点的坐标为或.
[解析]点拨:设点的坐标为,
如图,当为对角线时,四边形为平行四边形.
,,,
解得
点的坐标为;
当为对角线时,四边形为平行四边形.
,,,
解得
点的坐标为(不合题意,舍去);
当为对角线时,四边形是平行四边形.
,,,
解得
点的坐标为.
综上所述,在轴右侧存在一点,使得以点,,,为顶点的四边形是平行四边形,点的坐标为或.
第页/共页
